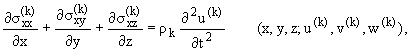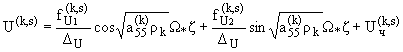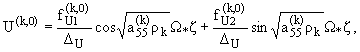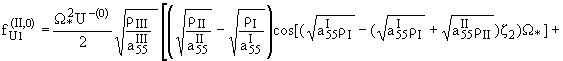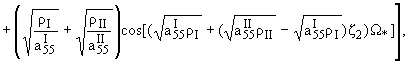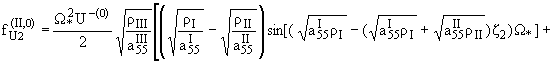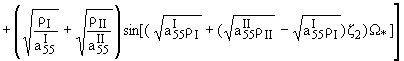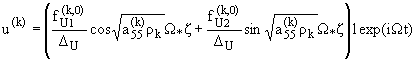ТЕОРИЯ УПРУГОСТИ
УДК 539.3, 624.15
Академик Л. А. Агаловян, Р. Ж. Оганесян
О характере вынужденных колебаний трёхслойной ортотропной
пластинки при смешанной краевой задаче
(Представлено 3/IV 2006)
Ключевые слова: вынужденные колебания, анизотропия, упругость, амплитуда, резонанс,
сейсмоизолятор
Получено асимптотически точное решение
пространственной смешанной задачи о вынужденных колебаниях трёхслойных
ортотропных пластин. Показано, что наличие мягкого среднего слоя приводит к
уменьшению амплитуд колебаний в вышестоящем слое. Теоретически обосновано
применение сейсмоизоляторов.
1. Рассмотрим
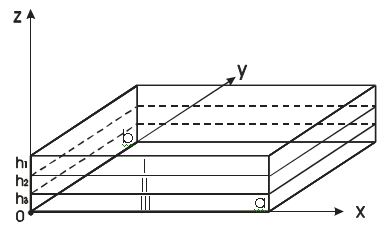
вынужденные колебания трёхслойной ортотропной пластинки: D = {(x,y,z) : x О [0,a], y О [0,b], 0 Ј z Ј h,
h = h1 + h2 + h3, h << min(a,b)} при условиях
полного контакта между слоями, когда верхняя грань верхнего слоя свободна, а на
лицевой поверхности нижнего слоя задан вектор перемещения, который во времени
изменяется гармонически (рис.1).
Имеем
граничные условия:
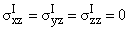 при z = h, при z = h, | |
(1.1) |
| uIII(z = 0) = u-(x,h)exp(iWt), | |
| vIII(z = 0) = v-(x,h)exp(iWt), | |
(1.2) |
| wIII(z = 0) = w-(x,h)exp(iWt), | |
| x = x/l,
h = y/l, l = |
min
|
(a,b) | |
и условия
полного контакта:
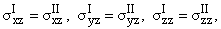 uI = uII, vI = vII, wI = wII при z = h2 + h3, uI = uII, vI = vII, wI = wII при z = h2 + h3, | |
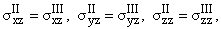 uII = uIII, vII = vIII, wII = wIII при z = h3. uII = uIII, vII = vIII, wII = wIII при z = h3. | |
(1.3) |
Рис.1.
Запишем систему динамических уравнений
пространственной задачи теории упругости анизотропного тела для ортотропных
сред:
|
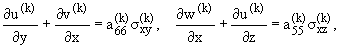
|
(1.4) |
|
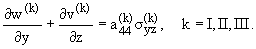
|
Решение системы уравнений (1.4) при граничных условиях (1.1), (1.2) и
условиях контакта (1.3) будем искать в виде [1,2]
|
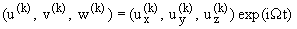
|
(1.5) |
| a, b =
x, y, z, m, j = 1, 2, 3, k = I, II, III. | |
Подставив (1.5) в (1.4), затем перейдя к безразмерным координатам и
безразмерным компонентам вектора перемещения:
| x =
x/l, h =
y/l, z =
z/h, | |
где
h = h1 + h2 + h3, hi - толщины слоёв,
l = min(a,b) и h << l, k - номер слоя, получим сингулярно возмущенную малым
параметром e = h/l систему, решение которой будем
искать в виде асимптотического разложения [3]:
| (U(k),V(k),W(k)) = es(U(k,s),V(k,s),W(k,s)), | |
s =
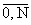 означает, что по немому
(повторяющемуся) индексу s происходит суммирование от 0 до числа приближений N.
Подставив (1.7) во вновь полученную систему уравнений, определив коэффициенты
разложения (1.7) и удовлетворив условиям (1.1) - (1.3), получим следующее
решение:
означает, что по немому
(повторяющемуся) индексу s происходит суммирование от 0 до числа приближений N.
Подставив (1.7) во вновь полученную систему уравнений, определив коэффициенты
разложения (1.7) и удовлетворив условиям (1.1) - (1.3), получим следующее
решение:
|
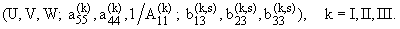 |
(1.8) |
Выражения
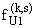 и
и
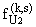 для произвольного s, а также значения величин
DU, DV, DW
приведены в [2].
для произвольного s, а также значения величин
DU, DV, DW
приведены в [2].
При s = 0 имеем
|
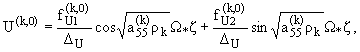 |
(1.9) |
где
|
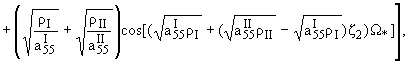 |
(1.10) |
Здесь z1 = (h1 + h2 + h3) / h = 1,
z2 = (h2 + h3) / h, z3 = h3 / h; U-(0) = u- / l,
V-(0) = v- / l, W-(0) = w- / l и
U-(s) = V-(s) = W-(s) = 0 при s
> 0.
Аналогично записываются выражения
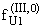 и
и
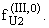
Считаем,
что DU, DV, DW № 0. Если W такова, что хотя бы
одна из этих величин равна нулю, произойдёт резонанс. Эти значения W совпадают со значениями частот собственных колебаний
[4].
2. Особый интерес представляет случай
| u- = const, v- = const,
w- = const. | |
(2.1) |
Уже приближению s = 0 соответствует точное решение:
|
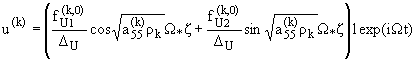 |
(2.2) |
Анализ
этого решения при различных конфигурациях слоёв пакета позволяет сделать весьма
важное для приложений, в частности для сейсмостойкого строительства,
заключение.
Рассмотрим трёхслойный пакет,
состоящий из слоёв СВАМ, стеклопластика СТЭТ и АСТТ, характеристики упругости
которых приведены в [3], с толщинами соответственно h1 = 0.3 м,
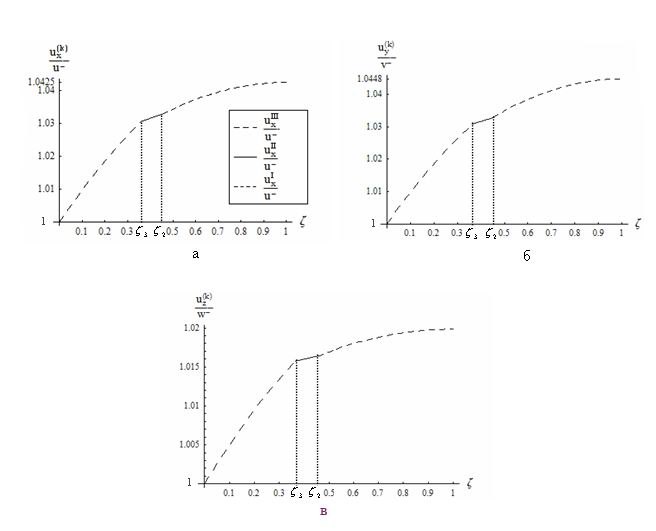
h2 = 0.05 м, h3 = 0.2 м. Графики амплитуд колебаний по толщине
пластинки приведены на рис. 2,а-в (сплошной линии соответствуют перемещения
среднего слоя II, пунктирным - перемещения слоёв I, III).
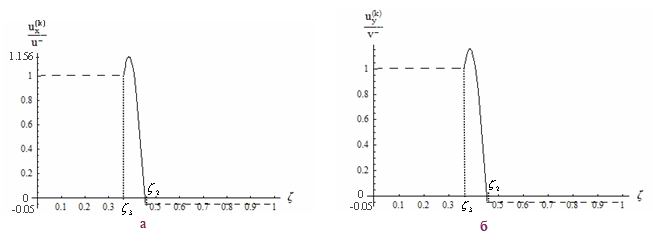
Рис.2 Теперь пусть верхний и нижний слои пакета состоят из слоёв
стеклопластика СВАМ и АСТТ соответственно, а средний слой из резины
(E = 6.96*105 Па, G = 2.4*105 Па, r = 1100 кг/м3). Этому будут соответствовать рис.
3, а-в.
Рис. 3 Аналогичная картина наблюдается, когда верхний и нижний слои из бетона,
а средний из резины.
Из приведённых графиков
видно, что если все три слоя состоят из жестких схожих материалов, то амплитуды
колебаний вырастают (хоть и незначительно) от слоя к слою. При наличии же
среднего слоя из более мягкого материала (например, резины), амплитуды колебаний
в верхнем слое резко уменьшаются. Этот результат сохраняет силу и при иных
толщинах среднего мягкого слоя. Установленный выше факт можно использовать в
сейсмостойком строительстве. Если при построении сооружений между бетонным
фундаментом и основанием вставить тонкий слой резины, это приведёт к уменьшению
опасных колебаний в фундаменте и, как следствие, к увеличению сейсмостойкости
сооружения.
3. Рассмотрим ту же задачу, но с
другими граничными условиями. Предполагается, что верхняя грань верхнего слоя
жёстко закреплена, т.е. в условиях (1.1) вместо
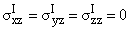 имеем
uI = vI = wI = 0 при z = h. В этом случае, опять - таки
решив уравнения (1.4) при изменённых граничных условиях, получим решение в виде
(1.8), но с другими функциями
имеем
uI = vI = wI = 0 при z = h. В этом случае, опять - таки
решив уравнения (1.4) при изменённых граничных условиях, получим решение в виде
(1.8), но с другими функциями
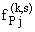 (P = U,V,W; j = 1,2; k = I,II,III). В частности, условиям (2.1) будет соответствовать
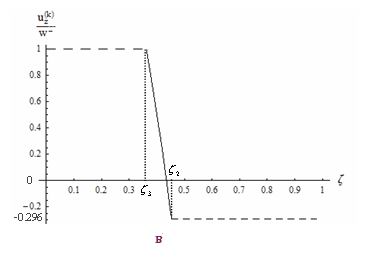
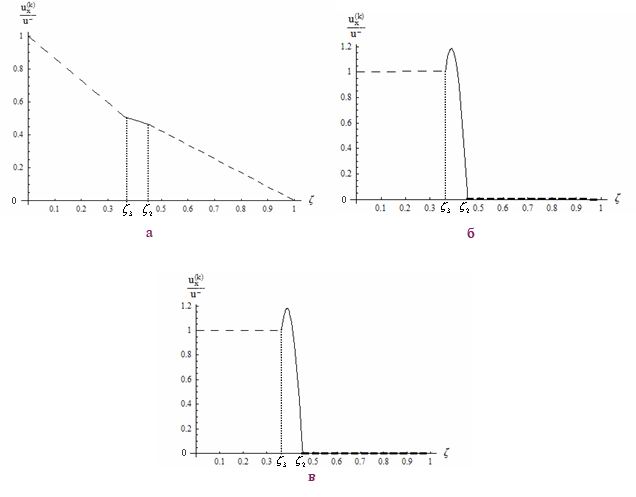
решение (1.8), (1.9), а в (1.10) необходимо заменить sin на (-cos), cos на sin. На рис. 4, а-в изображены изменения
амплитуд тангенциального смещения U по толщине пластинки при следующих
комбинациях пакета: СВАМ, СТЭТ, АСТТ; СВАМ, резина, АСТТ; бетон, резина,
бетон.
(P = U,V,W; j = 1,2; k = I,II,III). В частности, условиям (2.1) будет соответствовать
решение (1.8), (1.9), а в (1.10) необходимо заменить sin на (-cos), cos на sin. На рис. 4, а-в изображены изменения
амплитуд тангенциального смещения U по толщине пластинки при следующих
комбинациях пакета: СВАМ, СТЭТ, АСТТ; СВАМ, резина, АСТТ; бетон, резина,
бетон.
|
|
Рис.4
Как видно из графиков, в этом случае тоже амплитуды колебаний в верхнем
слое уменьшаются при наличии среднего слоя из резины.
Работа выполнена при поддержке INTAS, grant Ref. No: 03-51-5547.
Институт механики НАН РА
Литература
1. Агаловян Л. А. В сб.:
Проблемы механики тонких деформируемых тел. Ереван. Изд-во "Гитутюн" НАН РА.
2002. С. 9-19.
2. Оганесян Р. Ж. В сб.: Избранные вопросы теории упругости, пластичности и ползучести.
Ереван. Изд-во "Гитутюн" НАН РА. 2006. С. 242-248.
3. Агаловян Л. А. Асимптотическая теория анизотропных
пластин и оболочек. М. Наука. 1997. 415 с.
4. Агаловян Л. А., Оганесян Р. Ж. В сб.: V Междунар. конф.
"Проблемы динамики взаимодействия деформируемых сред." Ереван. Изд-во "Гитутюн"
НАН РА. 2005. С. 14-22.
![]() при z = h,
при z = h, ![]() uI = uII, vI = vII, wI = wII при z = h2 + h3,
uI = uII, vI = vII, wI = wII при z = h2 + h3,![]() uII = uIII, vII = vIII, wII = wIII при z = h3.
uII = uIII, vII = vIII, wII = wIII при z = h3.