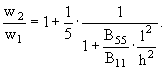МЕХАНИКА
УДК 531.8
Р. М. Киракосян
Влияние распределения касательных напряжений по толщине
пластинки при наличии касательных поверхностных нагрузок
(Представлено академиком Л. А. Агаловяном 26/VII 2006)
Ключевые слова: пластинка, ортотропия, поправочные коэффициенты, касательные напряжения,
форма распределения
Известно ([1]-[3] и др.), что если уточненная
теория пластин строится на основе гипотез для перемещений, то с целью повышения
точности вводятся поправочные коэффициенты Kx,Ky,
учитывающие влияние форм распределения касательных напряжений txz,tyz по
толщине пластинки. Если же теория пластин опирается на гипотезы для касательных
напряжений (например [4]), то законы распределения этих напряжений
непосредственно участвуют в построении теории и необходимость введения
поправочных коэффициентов автоматически отпадает.
B настоящей статье с использованием принципa виртуальных работ
обобщаются выражения коэффициентов Kx,Ky на случай
действия произвольных нагрузок. Используя эти выражения и опираясь на гипотезы
для перемещений, получeны соотношения и уравнения ортотропных пластин, которые
позволяют учитывать влияние форм распределения напряжений txz,tyz и при
наличии касательных поверхностных нагрузок. Приводятся примеры приложения.
Полученные результаты сравниваются с соответствующими результатами теории [5],
которая не учитывает влияния форм распределения напряжений txz,tyz по
толщине пластинки.
Литературу об истории
развития различных теорий пластин и оболочек, а также многочисленные их
приложения можно найти в монографиях [6]-[12] и др.
1. Рассмотрим прямоугольную ортотропную пластинку постоянной толщины h.
Координатную плоскость xoy совместим со срединной плоскостью пластинки, а ось oz
направим вертикально вниз. Главные направления анизотропии материала параллельны
координатным осям. Пластинка несет произвольные нагрузки. Проекции
интенсивностей поверхностных нагрузок на оси ox, oy, oz обозначим X±, Y±, Z±. Знаки ''+'' и ''-'' относятся к поверхностям z = +h/2
и z = -h/2 соответственно.
В качестве основополагающих гипотез примем:
а) перемещения по осям ox и oy, т.е. перемещения ux и
uy, являются линейными функциями поперечной координаты
z;
б) перемещение uz, нормальное к
срединной плоскости, по толщине пластинки не
меняется;
в) напряжение sz пренебрежительно
мало.
На основе этих допущений имеем:
Здесь u,v,w,j,y -
искомые функции.
В силу (1.1) основные
напряжения sx,sy,txy будут
иметь линейное распределение по толщине пластинки. Тогда согласно
дифференциальным уравнениям равновесия сплошной среды касательные напряжения
txz и tyz вдоль толщины пластинки будут изменяться по
закону квадратной параболы. Имея в виду это обстоятельство, после удовлетворения
условиям на поверхностях z = ±h/2 получим:
| txz = |
3Qx
2h
|
|
ж
з
и |
1 - |
4z2
h2
|
|
ц
ч
ш |
- |
X1
2
|
|
ж
з
и |
1 - |
12z2
h2
|
|
ц
ч
ш |
+ |
z
h
|
X2, | |
| tyz = |
3Qy
2h
|
|
ж
з
и |
1 - |
4z2
h2
|
|
ц
ч
ш |
- |
Y1
2
|
|
ж
з
и |
1 - |
12z2
h2
|
|
ц
ч
ш |
+ |
z
h
|
Y2, | |
Здесь Qx,Qy - поперечные силы,
| X1 = |
X+ - X-
2
|
, Y1 = |
Y+ - Y-
2
|
,
X2 = X+ + X-,
Y2 = Y+ + Y-. | |
(1.3) |
С
целью определения прогиба некоторой точки пластинки в этой точке по направлению
искомого прогиба мысленно приложим единичную силу. Возникшие от этой силы
касательные напряжения будут:
|
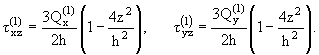
|
(1.4) |
Здесь
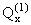 и
и
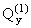 -
поперечные силы, вызванные действием единичной силы.
-
поперечные силы, вызванные действием единичной силы.
Согласно принципу виртуальных работ, работа единичной силы на том
перемещении данной точки пластинки, которое вызвано реально действую-щей
нагрузкой, равна суммарной работе напряжений, соответствующих единичной силе, на
действительных деформациях пластинки [2]. С целью определения вклада деформаций
поперчных сдвигов рассмотрим работу только напряжений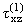 и
и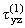 на соответствующих реальных
деформациях поперечных сдвигов gxz и gyz. Учитывая, что
на соответствующих реальных
деформациях поперечных сдвигов gxz и gyz. Учитывая, что
| gxz = |
txz
B55
|
, gyz = |
tyz
B44
|
, | |
(1.5) |
и имея в виду (1.2), (1.4), для
поправки к классическому значению прогиба после интегрирования по толщине
пластинки получим
|
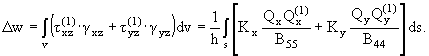
|
(1.6) |
Здесь B55,
B44 - модули сдвига материала в плоскостях xoz,yoz [4] , v - объем
пластинки, s - площадь ее срединной плоскости. Коэффициенты Kx и
Ky имеют выражения:
| Kx = |
6
5
|
- |
X1h
5Qx
|
, Ky = |
6
5
|
- |
Y1h
5Qy
|
. | |
(1.7) |
В
выражениях (1.7) параметры нагрузок X2 и Y2 не фигурируют,
поскольку относятся к плоской задаче, а не задаче изгиба пластинки. Если же не
учитывать влияния форм распределения напряжений txz,tyz по
толщине пластинки, т.е. вместо (1.2) использовать средние значения напряжений
|
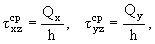
|
(1.8) |
то взамен (1.6) получится
|
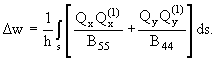
|
(1.9) |
Сравнивая (1.6) и (1.9), заключаем, что коэффициенты Kx и
Ky учитывают влияние форм распределения напряжений txz,tyz по
толщине пластинки. При отсутствии касательных поверхностных нагрузок
X1 = Y1 = 0 и коэффициенты Kx,Ky
принимают постоянное по всей пластинке известное значение ''6/5'' ([1]-[3] и
др.).
2. Значения приведенных деформаций
поперечных сдвигов
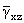 и
и
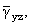 одинаковых для всех точек данного сечения
пластинки, определяются формулами
одинаковых для всех точек данного сечения
пластинки, определяются формулами
|
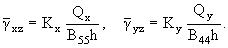
|
(2.1) |
С
другой стороны, в силу допущений (1.1) имеем:
|
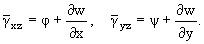
|
(2.2) |
Из
(2.1) и (2.2) для поперечных сил находим:
| Qx = |
5
6
|
B55h |
ж
з
и |
j + |
¶w
¶x
|
|
ц
ч
ш |
+ |
X1h
6
|
,
Qy = |
5
6
|
B44h |
ж
з
и |
y + |
¶w
¶x
|
|
ц
ч
ш |
+ |
Y1h
6
|
. | |
(2.3) |
Соотношения (2.3) вместе с допущениями (1.1) позволяют получить
уравнения пластин, способныx учитывать влияние форм распределения касательных
напряжений txz,tyz по толщине пластинки и при отсутствии
поперечных сил.
Пользуясь (1.1) и
соотношениями обобщенного закона Гука, при пренебрежении напряжениeм sz, для основных напряжений, моментов и остальных
усилий пластинки получим:
| sx = B11 |
¶u
¶x
|
+ B12 |
¶v
¶y
|
+ z |
ж
з
и |
B11 |
¶j
¶x
|
+ B12 |
¶y
¶y
|
|
ц
ч
ш |
, | |
| sy = B22 |
¶v
¶y
|
+ B12 |
¶u
¶x
|
+ z |
ж
з
и |
B22 |
¶y
¶y
|
+ B12 |
¶j
¶x
|
|
ц
ч
ш |
, | |
(2.4) |
| txy = B66 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
+ zB66 |
ж
з
и |
|
¶j
¶y
|
+ |
¶y
¶x
|
|
ц
ч
ш |
, | |
| Tx = C11 |
¶u
¶x
|
+ C12 |
¶v
¶y
|
,
Ty = C22 |
¶v
¶y
|
+ C12 |
¶u
¶x
|
, S = C66 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
, | |
(2.5) |
| Mx = D11 |
¶j
¶x
|
+ D12 |
¶y
¶y
|
,
My = D22 |
¶y
¶y
|
+ D12 |
¶j
¶x
|
, Mxy = D66 |
ж
з
и |
|
¶j
¶y
|
+ |
¶y
¶x
|
|
ц
ч
ш |
. | |
(2.6) |
Здесь, как обычно [4],
| Cij = Bijh,
Dij = |
Bijh3
12
|
, | |
(2.7) |
Bij - постоянные
материала.
Уравнения равновесия
дифференциального элемента срединной плоскости пластинки имеют вид [4]:
|
¶Tx
¶x
|
+ |
¶S
¶y
|
= -X2,
|
¶Ty
¶y
|
+ |
¶S
¶x
|
= -Y2, | |
|
¶Qx
¶x
|
+ |
¶Qy
¶y
|
= -Z2,
|
¶Mx
¶x
|
+ |
¶Mxy
¶y
|
= Qx - hX1, | |
(2.8) |
|
¶My
¶y
|
+ |
¶Mxy
¶x
|
= Qy - hY1, | |
где
Подставляя выражения усилий и моментов в (2.8), приходим к следующим
системам уравнений:
| C11 |
¶2u
¶x2
|
+ (C12 + C66) |
¶2v
¶x¶y
|
+ C66 |
¶2u
¶y2
|
= -X2, | |
| C22 |
¶2v
¶y2
|
+ (C12 + C66) |
¶2u
¶x¶y
|
+ C66 |
¶2v
¶x2
|
= -Y2, | |
(2.10) |
| B55 |
ж
з
и |
|
¶j
¶x
|
+ |
¶2 w
¶x2
|
|
ц
ч
ш |
+ B44 |
ж
з
и |
|
¶y
¶y
|
+ |
¶2 w
¶y2
|
|
ц
ч
ш |
= - |
6Z2
5h
|
- |
1
5
|
|
ж
з
и |
|
¶X1
¶x
|
+ |
¶Y1
¶y
|
|
ц
ч
ш |
, | |
| D11 |
¶2j
¶x2
|
+ (D12 + D66) |
¶2y
¶x¶y
|
+ D66 |
¶2j
¶y2
|
- |
5
6
|
B55h |
ж
з
и |
j + |
¶w
¶x
|
|
ц
ч
ш |
= - |
5X1h
6
|
, | |
(2.11) |
| D22 |
¶2y
¶y2
|
+ (D12 + D66) |
¶2j
¶x¶y
|
+ D66 |
¶2y
¶x2
|
- |
5
6
|
B44h |
ж
з
и |
y + |
¶w
¶y
|
|
ц
ч
ш |
= - |
5Y1h
6
|
. | |
Система уравнений (2.10) относится к плоской задаче, а (2.11) - к задаче
изгиба пластинки. Первая система имеет четвертый, а вторая - шестой порядок. В
соответствии с этим на каждом краю пластинки следует ставить по пять краевых
условий: по два условия для плоской задачи и по три - для задачи изгиба. Плоская
задача и задача изгиба пластинки разделяются друг от друга и можно решить их в
отдельности.
Приведем некоторые, наиболее
часто встречающиеся условия для краев x = const.
а) Условия свободного края:
| C11 |
¶u
¶x
|
+ C12 |
¶v
¶y
|
= 0
(Tx = 0), |
¶u
¶y
|
+ |
¶v
¶x
|
= 0 (S = 0), | |
(2.12) |
| D11 |
¶j
¶x
|
+ D12 |
¶y
¶y
|
= 0 (Mx = 0), | |
|
¶j
¶y
|
+ |
¶y
¶x
|
= 0 (Mxy = 0), | |
| 5B55 |
ж
з
и |
j + |
¶w
¶x
|
|
ц
ч
ш |
+ X1 = 0 (Qx = 0). | |
б) Условия свободного шарнирного опирания: первые четыре условия
совпадают с соответствующими условиями свободного края. Взамен последнего
условия (2.13) следует брать
в) Условия заделанного края:
Возможны
и другие условия. Аналогичным образом можно написать условия и для краев y =
const.
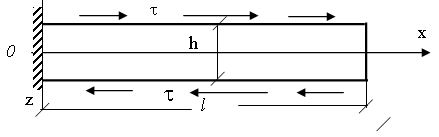
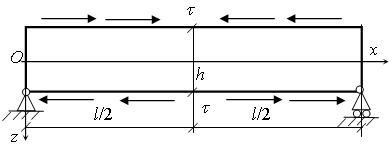
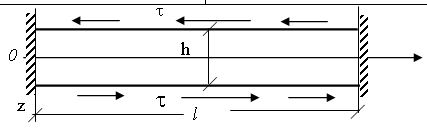
3. В приведенной таблице представлены
решения трех задач для пластинки - полосы, полученные на основе уравнений (2.11)
и по теории [5] при действии только касательных поверхностных нагрузок.
Результаты, соответствующие уравнениям (2.11), снабжены индексом ''1'', а теории
[5] - индексом ''2''. Отметим, что теория [5] не учитывает влияния форм
распределения касательных напряжений txz,
tyz по толщине пластинки. Она фактически
учитывает влияние средних значений этих напряжений. Поэтому в случаях отсутствия
поперечных сил, когда средние значения напряжений txz, tyz, а
следовательно, и средние значения соответствующих деформаций поперечных сдвигов
равны нулю, теория [5] поправки не дает и ее результаты совпадают с
соответствующими результатами теории Кирхгофа. Такая ситуация имеет место в
первых двух рассмотренных задачах. Уравнения же (2.11) в этих случаях дают
определенные поправки. Например, для полос из углепластика [4] при
поправка к значению наибольшего
прогиба по уравнениям (2.11) составляет:
в
первой задаче D1 = 0.08,
во
второй задаче D1 = 0.32.
В
третьей задаче уравнения (2.11) и теория [5] приводят к качественно подобным
результатам. Они отличаются лишь количественно. Значения прогибов по теории [5]
получаются больше -
|
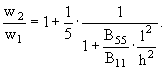
|
(3.2) |
При (3.1) это отношение составляет 1.123. Когда B55 ® Ґ, решения по обоим способам
стремятся к решению по теории Кирхгофа:
| по уравнениям (2.11) |
по теории [5] |
|
W1 = [(th)/(6D11)]x2(3l-x)+[(tx)/(6B55)]
|
W2 = [(th)/(6D11)]x2(3l-x) |
|
W1max = [(thl3)/(3D11)](1+[1/20][(B11)/(B55)]·[(h2)/(l2)]),
D1 = [1/20][(B11)/(B55)]·[(h2)/(l2)] |
W2max = [(thl3)/(3D11)],
D2 = 0 |
| по уравнениям (2.11) |
по теории [5] |
| W1 = [(th)/(24D11)]x(3l2-4x2)+[(tx)/(5B55)], 0 Ј x
Ј l/2 |
W2 = [(th)/(24D11)]x(3l2-4x2), 0 Ј x Ј l/2 |
| W1 = [(th(l-x))/(24D11)](8lx-4x2-l2)+[(t(l-x))/(5B55)] |
W2 = [(th(l-x))/(24D11)](8lx-4x2-l2), |
| l/2 Ј x Ј l |
l/2 Ј x Ј l |
| W1max = [(thl3)/(24D11)](1+[1/5][(B11)/(B55)]·[(h2)/(l2)]),
D1 = [1/5][(B11)/(B55)]·[(h2)/(l2)] |
W2max = [(thl3)/(24D11)], D2 = 0 |
| по уравнениям (2.11) |
по теории [5] |
| W1 = [(5thx(l2-3lx+2x2))/(72D11+5B55hl2)]
|
W2 = [(thx(l2-3lx+2x2))/(12D11+B55hl2)]
|
W1max = |W1|,
(x = [l/2](1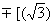 /3])) /3])) |
W2max = |W2|,
(x = [l/2](1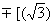 /3])) /3])) |
| Q1 = th[(12D11+5B55hl2)/(72D11+5B55hl2)] |
Q2 = th[(B55hl2)/(12D11+B55hl2)] |
| M1 = [(30thD11(l-2x))/(72D11+5B55hl2)] |
M2 = [(6D11th(l-2x))/(12D11+B55hl2)] |
Институт механики НАН РА
Литература
1. Reissner E. T - Trans.
ASME. 1945. V. 67. P. A69-A77.
2. Тимошенко
С. П., Гере Дж. Механика материалов. М. Миp. 1976. 669
с.
3. Григоренко Я. М., Василенко А. Т. Теория оболочек переменной жесткости. Киев. Наукова думка. 1981.
544 с.
4. Амбарцумян С. А. Теория анизотропных пластин. М. Наука. 1987. 360 с.
5. Васильев В. В. - Изв. АН
МТТ. 1998. №3. C. 46-58.
6. Агаловян Л. А. Асимптотическая теория анизотропных пластин и оболочек. М. Наука.
1997. 414 с.
7. Лурье А. И. Статика тонкостенных упругих оболочек. М. Гостехиздат. 1947. 251с.
8. Лехницкий С. Г. Анизотропные пластинки. М. Гостехиздат. 1957. 463 с.
9. Новожилов В. В. Теория
тонких оболочек. Л. Судпромгиз. 1962. 431 с.
10. Тимошенко С. П., Войновский-Кригер С. Пластинки и
оболочки. М. Физматгиз. 1963. 635 с.
11.
Пелех Б. Л. Теория оболочек с конечной сдвиговой жесткостью. Киев.
Наукова думка. 1973. 248 с.
12.
Гольденвейзер А. Л. Теория упругих тонких оболочек. М. Наука.
1976. 510 с.
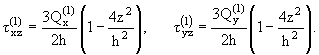
![]() и
и
![]() -
поперечные силы, вызванные действием единичной силы.
-
поперечные силы, вызванные действием единичной силы.![]() и
и![]() на соответствующих реальных
деформациях поперечных сдвигов gxz и gyz. Учитывая, что
на соответствующих реальных
деформациях поперечных сдвигов gxz и gyz. Учитывая, что
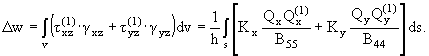
![]()
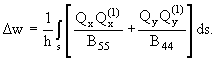
![]() и
и
![]() одинаковых для всех точек данного сечения
пластинки, определяются формулами
одинаковых для всех точек данного сечения
пластинки, определяются формулами
![]()
![]()