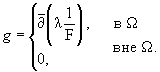1. Работа посвящена исследованию множеств
пика и тесно связанных с ними множеств интерполяции для алгебр Am,a(Un). Приведем
необходимые определения. Пусть
Un = {z = (z1, ј, zn) О Cn
: |zi| <
1, i = 1, ј, n} - единичный полидиск
в
пространстве Cn;
Tn={z
О Cn : |zi| = 1, i = 1, ј,
n} - его остов.
Для заданного целого
числа m, m і 0, и a О (0,1] обозначим через Am(Un) алгебру функций, голоморфных в
Un, производные которых порядка m непрерывно
продолжаются на замыкание Un, и через
Am,a(Un) -
подалгебру Am(Un), состоящую из
функций, у которых производные порядка m удовлетворяют в Un условию
Гёльдера порядка a. Аналогично обозначаются подалгебры
Cm(Tn) и Cm,a(Tn) алгебры
C(Tn) функций, непрерывных на
остове Tn.
Компактное
подмножество K остова называется множеством пика для
Am(Un) или Am,a(Un), если существует
функция f О Am,a(Un) (соответственно,
f О Am,a(Un)) такая, что f = 1 на K и |f(z)| < 1 для всех z О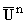 \K.
\K.
Это
условие можно задать в эквивалентной форме: существует функция f такая, что
f(z) = 0, при z О K, и Re f(z) >
0 при z О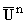 \K. \K. |
|
(1) |
Компакт K называется интерполяционным множеством
для Am(Un) или Am,a(Un), если для каждой
функции f из Cp(TN) (соответственно,
Cp,a(TN)) существует F
О Am(Un) (F
О Am,a(Un)), которая равна f
на K.
2. Задаче
описания множеств пика и интерполяции для различных функциональных алгебр
посвящено немало работ. Наиболее полно исследован случай полидиск-алгебры
A(Un) = A0(Un). Хорошо известно (см. например [1]), что множества
пика и интерполяции K М Tn характеризуются
тем, что вариация любой ортогональной меры на них равна
нулю, т. е. условие |m(K)| = 0 выполняется для всякой
борелевской меры m на TN такой, что m^A(Un). Согласно классической теореме М. и Ф. Риссов,
всякая мера, ортогональная к диск-алгебре A(U), абсолютно
непрерывна. Поэтому в одномерном случае (т. е. n = 1) множества пика и
интерполяции для A(U) суть замкнутые подмножества
окружности лебеговой меры нуль.
Для алгебр
гладких функций (т. е. при m і 1) дело обстоит иначе.
Уже в одномерном случае множества пика и интерполяции не совпадают: множества
пика конечны, (см. [2]), а интерполяционные множества могут быть и бесконечными
и определяются условием, которое дано в [3].
Многомерный случай исследован меньше. Для формулировки результатов нам
нужно следующее понятие.
Определение. Гладкое подмногообразие M остова Tn
называется интерполяционным многообразием, если в каждой
точке q О M касательное пространство Tq(M)
пересекается с замкнутым положительным конусом Cq на
Tq(Tn), образованным касательными векторами
| ¶/¶q1|q, ј, ¶/¶qn|q,
qi = arg zi. | |
только
в начале координат.
Отметим, что, очевидно,
размерность M не превосходит n - 1.
3. В работах [4] и [5] доказано следующее необходимое условие:
если K является множеством пика для Am(Un), m і 1,
то в некоторой
окрестности множества K существует интерполяционное многообразие M гладкости
Cm такое, что K М M. Интересно
отметить, что этот результат неулучшаем в том смысле, что в общем случае не
существует замкнутого подмногообразия M остова с
перечисленными свойствами. В статье приведен соответствующий
пример.
В [4] исследована также достаточность
этого условия и доказано, что всякое компактное подмножество
интерполяционного многообразия класса Cm является множеством
пика для Am-4(Un). В теореме 1 этот результат
усиливается.
Теорема 1. Всякое компактное подмножество интерполяционного подмногообразия
класса Cm,a, m і 3, на остове полидиска Un является множеством пика для Am-1,a (Un).
Доказательство теоремы 1 основано на конструкции так называемой "почти
аналитической" функции пика (теорема 2), а также на оценке роста производных
решения соответствующего
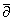 -уравнения при подходе к особенностям правой части (лемма
2). При этом достаточно ограничиться компактными подмножествами
интерполяционного подмногообразия, имеющего максимально возможную размерность,
т. е. n - 1. Это следует из следующей
леммы:
-уравнения при подходе к особенностям правой части (лемма
2). При этом достаточно ограничиться компактными подмножествами
интерполяционного подмногообразия, имеющего максимально возможную размерность,
т. е. n - 1. Это следует из следующей
леммы:
Лемма 1. Пусть M - интерполяционное Cm,a-гладкое подмногообразие остова Tn,
имеющее
размерность k, k Ј n - 1. Тогда на Tn существует (n - 1) -мерное интерполяционное подмногообразие той же
гладкости и такое, что M М
той же
гладкости и такое, что M М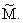
Теорема
2. Пусть M - интерполяционное подмногообразие размерности
n - 1 остова полидиска класса Cm,a, m і 3, K - компакт на M.
Тогда в некоторой окрестности W этого компакта
существуют функция F О Cm,a(W) и константа g > 0 такие, что
a)
F(z) = 0 тогда и только тогда, когда z О
K;
b) Re, F(z) і
gd(z, M)2 (z О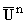 З W), где d(z, M) - расстояние между z
и M;
З W), где d(z, M) - расстояние между z
и M;
c)
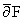 = O[d(z, M)]m-1+a;
= O[d(z, M)]m-1+a;
d) |F(z)| і
gd(z, M) (z О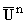 З W).
З W).
Доказательство. Пусть D - строго псевдовыпуклая
область с границей класса Cm,a, в
которую полидиск Un вложен следующим
образом:
1°
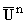 \Tn М
D,
\Tn М
D,
2° Tn М ¶D,
3° Tz(M) М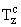 (¶D) для всех z О M
(¶D) для всех z О M
где
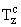 (¶D) - комплексная
гиперплоскость, содержащаяся в Tz(¶D).
Условие 3° означает, что M является
комплексно-касательным подмногообразием ¶D. Способ
построения такой области D изложен в [6].
(¶D) - комплексная
гиперплоскость, содержащаяся в Tz(¶D).
Условие 3° означает, что M является
комплексно-касательным подмногообразием ¶D. Способ
построения такой области D изложен в [6].
Далее, в работе [7] (см. также [8]) доказано, что в некоторой
окрестности W компакта K существует ''почти
аналитическая'' функция пика F, удовлетворяющая условиям a) и b) для области D,
и, следовательно, для вложенного в D полидиска Un. Кроме этого,
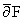 = 0 на W З M вместе со всеми производными порядка до m - 1 включительно. Поскольку
= 0 на W З M вместе со всеми производными порядка до m - 1 включительно. Поскольку
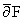 О Cm-1,a(W), то
О Cm-1,a(W), то
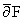 (z) = O[d(z,M)]m-1+a, т. е. имеет место c).
(z) = O[d(z,M)]m-1+a, т. е. имеет место c).
Отметим, что F = u + iv обладает также следующим свойством:
| grad u(z) = - |
cz
|cz||2
|
и grad v(z) = - |
tz
|tz||2
|
, | |
(2) |
где cz - вещественная нормаль в точке z к границе
области D, tz = Jcz, а J - оператор в R2n, который соответствует умножению на мнимую единицу
i в пространстве Cn
≃ R2n.
Чтобы
доказать свойство d), достаточно показать, что для любой точки z О M вдоль направления, касательного к остову и ортогонального
к Tz(M), производная функции F отлична от
нуля.
В самом деле, из условия M М ¶D следует, что
Tz(M) ^ cz. Так как M имеет комплексно-касательное
направление на ¶D, то JTz(M) М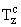 (¶D),
поэтому JTz(M) ^ cz, или, что то же, Tz(M) ^ tz. Очевидно,
(¶D),
поэтому JTz(M) ^ cz, или, что то же, Tz(M) ^ tz. Очевидно,
| Tz(Tn) ^ JTz(Tn)
и Tz(Tn) |
Е
|
JTz(Tn) = R2n. | |
(3) |
Из
(3) следует, что Tz(M) ^ JTz(M) и
размерность Tz(M) Е JTz(M)
составляет 2n - 2. Таким образом, Tz(M) Е JTz(M) является ортогональным дополнением в R2n комплексной нормали
 = R[cz] Е R[tz] к ¶D в точке z.
= R[cz] Е R[tz] к ¶D в точке z.
Пусть вектор
x касателен к остову в точке z, т. е. x О
Tz(Tn), и ортогонален к Tz(M).
Из (3) следует, что x ортогонален также и к
Tz(M) Е JTz(M), поэтому x О С другой стороны, x ^ tz, откуда следует, что вектор x параллелен tz. Так как
согласно (2) tz направлен вдоль градиента v,
то xv № 0, следовательно,
xF № 0, т. е. вдоль
направления x производная F отлична от
нуля.
С другой стороны, x ^ tz, откуда следует, что вектор x параллелен tz. Так как
согласно (2) tz направлен вдоль градиента v,
то xv № 0, следовательно,
xF № 0, т. е. вдоль
направления x производная F отлична от
нуля.
Замечание. Обратим
внимание на то, что в неравенстве d) d(z,M) участвует в первой, а не во второй
степени, как это имеет место в случае строго псевдовыпуклой области. Это
улучшение оценки является следствием того, что в отличие от границы строго
псевдовыпуклой области остов полидиска не имеет комплексных касательных
векторов.
Пусть K - компактное подмножество
интерполяционного многообразия M, окрестность W и
функция F удовлетворяют заключению теоремы 2. Пусть, далее, l - вещественная функция класса CҐ с носителем внутри W такая,
что 0 Ј l Ј 1 и l = 1 в некоторой окрестности
множества K. Определим (0,1)-форму g на
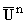 \K
\K
|
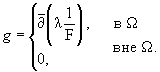
|
Лемма 2. В области Un
уравнение
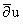 = g имеет решение u(z), бесконечно дифференцируемое на
множестве
= g имеет решение u(z), бесконечно дифференцируемое на
множестве
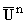 \M и удовлетворяющее условиям:
\M и удовлетворяющее условиям:
1° ¶|p|u(z)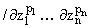 ограничена в Un при 0 Ј |p| Ј m - 3;
ограничена в Un при 0 Ј |p| Ј m - 3;
2° ¶
|p|u(z)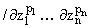 = O[d(z, M)]m-3-|p|+a при m - 2 Ј |p| Ј
m.
= O[d(z, M)]m-3-|p|+a при m - 2 Ј |p| Ј
m.
При доказательстве использованы формулы из
[9] для решения
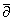 -уравнения в полидиске, а также рекурpентные формулы для
производных, полученные в [10].
-уравнения в полидиске, а также рекурpентные формулы для
производных, полученные в [10].
Доказательство теоремы 1. Пусть компакт K М M. В силу леммы 1 можно считать, что M имеет размерность
n - 1. Пусть, далее, функции F(z) и u(z) те же, что в
теореме 2 и лемме 2. Рассмотрим функцию
Имеем
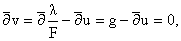 т. е. v(z) голоморфна в области Un.
т. е. v(z) голоморфна в области Un.
Далее,
| Re v = l |
Re F
|f|2
|
- Re u. | |
(4) |
Согласно лемме 2, функция u(z)
ограничена на
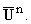 Поэтому с учетом пункта b) теоремы 2 из (4) имеем
Поэтому с учетом пункта b) теоремы 2 из (4) имеем
Re v(z) і
-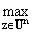 Re u(z) > -Ґ. Re u(z) > -Ґ. |
|
Добавив
в случае необходимости к функции u(z) соответствующую константу, можно считать,
что
Re v(z) > 0 при z О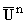 \K. \K. |
|
(5) |
Покажем, что функция
| f(z) = |
1
v(z)
|
= |
F(z)
l(z) - u(z)F(z)
|
| |
(6) |
является искомой функцией пика.
Прежде всего f(z) голоморфна в Un и, как следует
из (5) и (6), Re f(z) > 0 при z О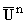 \K. Далее, нули f(z)
совпадают с нулями F(z), т.е. ввиду пункта a) теоремы 2, с множеством K. Таким
образом, f удовлетворяет условиям (1). Остается проверить, что f О Am-1,a(Un). В силу теоремы
Харди-Литтлвуда достаточно показать, что Djf(z) = O[d(z,M)]a-1 для любого целочисленного
вектора j такого, что |j| = m.
Функция f на множестве
\K. Далее, нули f(z)
совпадают с нулями F(z), т.е. ввиду пункта a) теоремы 2, с множеством K. Таким
образом, f удовлетворяет условиям (1). Остается проверить, что f О Am-1,a(Un). В силу теоремы
Харди-Литтлвуда достаточно показать, что Djf(z) = O[d(z,M)]a-1 для любого целочисленного
вектора j такого, что |j| = m.
Функция f на множестве
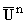 \K бесконечно дифференцируема, поэтому достаточно
рассмотреть ее лишь в окрестности множества K, где имеем
\K бесконечно дифференцируема, поэтому достаточно
рассмотреть ее лишь в окрестности множества K, где имеем
| f(z) = |
F(z)
1 - u(z)F(z)
|
. | |
Выражение для
Djf содержит производные Dpu, |p| = 0,1, ј, m. Согласно лемме 2 при 0 Ј |p| Ј
m - 3 они ограничены, а при |p| = m - 2
имеют порядок роста O[d(z,M)]a-1. С другой стороны, согласно той же лемме,
производные Dpu порядка |p| = m - 1 и |p| = m при подходе к M имеют больший
порядок роста, а именно, O[d(z,M)]a-2 и O[d(z,M)]a-3 соответственно. Нетрудно убедиться в том, что
слагаемые в выражении Djf, которые содержат эти производные, имеют
соответствующие сомножители F и F2, которые ''гасят'' излишний рост,
поэтому согласно пункту d) теоремы 2 указанные слагаемые также имеют порядок
роста O[d(z,M)]a-1.
Следствие.
Всякое компактное подмножество
интерполяционного подмногообразия класса Cm, m і 4, на остове полидиска Un является множеством пика для Am-2,1 (Un).
Далее
доказана следующая интерполяционная
Теорема 3. Пусть m і 3,
a О (0,1) и пусть K -
компактное подмножество интерполяционного подмногообразия гладкости
Cm,a на остове Tn полидиска
Un. Тогда
a) для заданной f О
Cm(Tn) существует функция F О Am-1,a(Un) такая, что F|K = f|K,
b) для
заданной f О Cm-1,a(Tn) существует
функция F О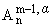 (Un) такая, что F|K = f|K.
(Un) такая, что F|K = f|K.
В
утверждении (b) под
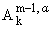 подразумевается подмножество функций из Am-1, у которых все производные порядка m - 1 допускают модуль непрерывности gda(log[1/(d)])k-1, где g - некоторая
константа. Таким образом, например,
подразумевается подмножество функций из Am-1, у которых все производные порядка m - 1 допускают модуль непрерывности gda(log[1/(d)])k-1, где g - некоторая
константа. Таким образом, например,
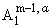 = Am-1,a.
= Am-1,a.
Ереванский государственный
университет
Институт математики НАН РА
![]() \K.
\K.![]() -уравнения при подходе к особенностям правой части (лемма
2). При этом достаточно ограничиться компактными подмножествами
интерполяционного подмногообразия, имеющего максимально возможную размерность,
т. е. n - 1. Это следует из следующей
леммы:
-уравнения при подходе к особенностям правой части (лемма
2). При этом достаточно ограничиться компактными подмножествами
интерполяционного подмногообразия, имеющего максимально возможную размерность,
т. е. n - 1. Это следует из следующей
леммы:![]() той же
гладкости и такое, что M М
той же
гладкости и такое, что M М![]()
![]() З W), где d(z, M) - расстояние между z
и M;
З W), где d(z, M) - расстояние между z
и M;![]() = O[d(z, M)]m-1+a;
= O[d(z, M)]m-1+a;![]() З W).
З W).![]() \Tn М
D,
\Tn М
D,![]() (¶D) для всех z О M
(¶D) для всех z О M![]() (¶D) - комплексная
гиперплоскость, содержащаяся в Tz(¶D).
Условие 3° означает, что M является
комплексно-касательным подмногообразием ¶D. Способ
построения такой области D изложен в [6].
(¶D) - комплексная
гиперплоскость, содержащаяся в Tz(¶D).
Условие 3° означает, что M является
комплексно-касательным подмногообразием ¶D. Способ
построения такой области D изложен в [6].![]() = 0 на W З M вместе со всеми производными порядка до m - 1 включительно. Поскольку
= 0 на W З M вместе со всеми производными порядка до m - 1 включительно. Поскольку
![]() О Cm-1,a(W), то
О Cm-1,a(W), то
![]() (z) = O[d(z,M)]m-1+a, т. е. имеет место c).
(z) = O[d(z,M)]m-1+a, т. е. имеет место c).![]() (¶D),
поэтому JTz(M) ^ cz, или, что то же, Tz(M) ^ tz. Очевидно,
(¶D),
поэтому JTz(M) ^ cz, или, что то же, Tz(M) ^ tz. Очевидно, ![]() = R[cz] Е R[tz] к ¶D в точке z.
= R[cz] Е R[tz] к ¶D в точке z.![]() С другой стороны, x ^ tz, откуда следует, что вектор x параллелен tz. Так как
согласно (2) tz направлен вдоль градиента v,
то xv № 0, следовательно,
xF № 0, т. е. вдоль
направления x производная F отлична от
нуля.
С другой стороны, x ^ tz, откуда следует, что вектор x параллелен tz. Так как
согласно (2) tz направлен вдоль градиента v,
то xv № 0, следовательно,
xF № 0, т. е. вдоль
направления x производная F отлична от
нуля.![]() \K
\K ![]() = g имеет решение u(z), бесконечно дифференцируемое на
множестве
= g имеет решение u(z), бесконечно дифференцируемое на
множестве
![]() \M и удовлетворяющее условиям:
\M и удовлетворяющее условиям:![]() ограничена в Un при 0 Ј |p| Ј m - 3;
ограничена в Un при 0 Ј |p| Ј m - 3;![]() = O[d(z, M)]m-3-|p|+a при m - 2 Ј |p| Ј
m.
= O[d(z, M)]m-3-|p|+a при m - 2 Ј |p| Ј
m.![]() -уравнения в полидиске, а также рекурpентные формулы для
производных, полученные в [10].
-уравнения в полидиске, а также рекурpентные формулы для
производных, полученные в [10].![]() \K. Далее, нули f(z)
совпадают с нулями F(z), т.е. ввиду пункта a) теоремы 2, с множеством K. Таким
образом, f удовлетворяет условиям (1). Остается проверить, что f О Am-1,a(Un). В силу теоремы
Харди-Литтлвуда достаточно показать, что Djf(z) = O[d(z,M)]a-1 для любого целочисленного
вектора j такого, что |j| = m.
Функция f на множестве
\K. Далее, нули f(z)
совпадают с нулями F(z), т.е. ввиду пункта a) теоремы 2, с множеством K. Таким
образом, f удовлетворяет условиям (1). Остается проверить, что f О Am-1,a(Un). В силу теоремы
Харди-Литтлвуда достаточно показать, что Djf(z) = O[d(z,M)]a-1 для любого целочисленного
вектора j такого, что |j| = m.
Функция f на множестве
![]() \K бесконечно дифференцируема, поэтому достаточно
рассмотреть ее лишь в окрестности множества K, где имеем
\K бесконечно дифференцируема, поэтому достаточно
рассмотреть ее лишь в окрестности множества K, где имеем ![]() (Un) такая, что F|K = f|K.
(Un) такая, что F|K = f|K.![]() подразумевается подмножество функций из Am-1, у которых все производные порядка m - 1 допускают модуль непрерывности gda(log[1/(d)])k-1, где g - некоторая
константа. Таким образом, например,
подразумевается подмножество функций из Am-1, у которых все производные порядка m - 1 допускают модуль непрерывности gda(log[1/(d)])k-1, где g - некоторая
константа. Таким образом, например,
![]() = Am-1,a.
= Am-1,a.