МАТЕМАТИКА
УДК: 517.98
Г. А. Саргсян
О собственных функциях, порожденных однородной задачей
Неймана,
для одного дифференциального пучка
(Представлено академиком А. А. Талаляном 6/VI 2006)
Ключевые слова: смешанная задача, полнота, квадратичный пучок, собственная
функция
В работе изучается краевая задача на
собственные значения:
| Ll(u) = |
¶2u
¶y2
|
+ 2l |
¶2u
¶x¶y
|
+ l2Du = 0, | |
(1) |
| Gu = au + |
¶u
¶n
|
|
к
к
к¶W |
= 0, | |
(2) |
где W -
круг с центром в начале координат, ¶W - единичная окружность, D -
двумерный оператор Лапласа, n - внешняя нормаль к окружности ¶W, a і 0 - постоянное число. Собственным значением задачи (1), (2)
назовем число l, при котором существует функция
ul, удовлетворяющая (1), (2), отличная от
постоянной при a = 0 и отличная от тождественного нуля
при a > 0. В [1] рассмотрена однородная краевая
задача Дирихле на собственные значения:
|
¶2u
¶y2
|
+ 2l |
¶2u
¶x¶y
|
+ l2Du = 0, | |
(3) |
где путем построения рекуррентных
формул доказано существование полной системы полиномиальных собственных функций
в комплексном соболевском гильбертовом пространстве
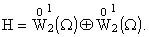
В [2]
приводится явное представление полной совокупности полиномиальных собственных
функций задачи (3), (4) в соболевском пространстве
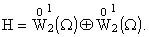
Для построения
полной системы решений уравнения (1) удобнее построить системы решений этого
уравнения, обращающихся в нуль на границе круга и являющихся полиномaми по x,y.
В дальнейшем для наших построений и формулировки полученных результатов удобно
перейти от действительных x,y к комплексным переменным z = x + iy, z = x - iy, и использовать комплексные операторы дифференцирования
|
¶
¶z
|
= |
1
2
|
|
ж
з
и |
|
¶
¶x
|
- i |
¶
¶y
|
|
ц
ч
ш |
, |
¶
¶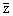
|
| 1
2
|
|
ж
з
и |
|
¶
¶x
|
+ i |
¶
¶y
|
|
ц
ч
ш |
. | |
Тогда краевую задачу (1), (2) можно записать в комплексной форме
|
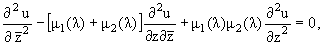
|
(5) |
|
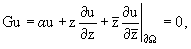
|
(6) |
где
| m1(l) = 1 - 2li m2(l) = |
1
1 + 2li
|
. | |
(7) |
Нами
установлена двукратная полнота системы полиномиальных собственных функций задачи
(1), (2) в гильбертовом пространстве H при a > 0;
когда же a = 0, двукратная полнота собственных функций
в соответствующем пространстве уже не имеет местa.
Наряду с краевой задачей (5), (6) будем рассматривать следующую
спектральную задачу Дирихле:
|
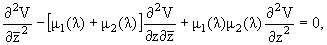
|
(8) |
Легко убедиться, что задача (5), (6) тесно связана с задачей Дирихле
(8), (9), а именно, что собственные значения задачи (5), (6) одновременно
являются и собственными значениями задачи Дирихле и - наоборот, если a № -l,
l = 1, 2, 3, ... Обозначим систему полиномиальных решений задачи (8), (9) через
|
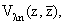
|
(10) |
что соответствует собственным
значениям ln.
Заметим, что система (10) в соболевском пространстве
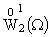 является двукратно полной в смысле М. В. Келдыша
[3]. Перейдем теперь к решению задачи (5), (6). Она состоит в нахождении функций
из класса C2(W) И C1(W), удовлетворяющих
уравнению (5) в круге
является двукратно полной в смысле М. В. Келдыша
[3]. Перейдем теперь к решению задачи (5), (6). Она состоит в нахождении функций
из класса C2(W) И C1(W), удовлетворяющих
уравнению (5) в круге
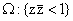 и граничным условиям (6) на границе
и граничным условиям (6) на границе
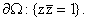
В дальнейшем для
наших построений существенную роль будут играть следующие полиномы:
|
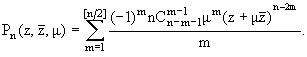
|
(11) |
Приведем две вспомогательные леммы без доказательства, установленные
нами в [2], характеризующие свойства полиномов Pn(z,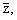 m), которые используются в
дальнейшем.
m), которые используются в
дальнейшем.
Лемма 1. Полиномы Pn(z,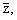 m) при n = 2, 3, ... удовлетворяют рекуррентному
соотношению
m) при n = 2, 3, ... удовлетворяют рекуррентному
соотношению
|
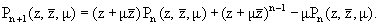
|
(12) |
Лемма 2. Полиномы
Pn(z,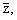 m) на
окружности круга W удовлетворяют рекуррентному
соотношению
m) на
окружности круга W удовлетворяют рекуррентному
соотношению
|
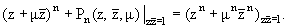
|
(13) |
Общее решение уравнения (5) при любом значении параметра l имеет вид
|
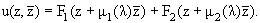
|
(14) |
Перейдем к построению в явном виде полной совокупности нетривиальных
полиномиальных решений краевой задачи (5), (6) при a
> 0. Легко проверить, что
GQn(z,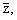 m) = Pn(z, m) = Pn(z,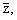 m), m), |
|
(15) |
где
|
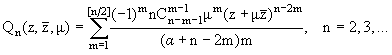
|
(16) |
Рассмотрим последовательность функции
|
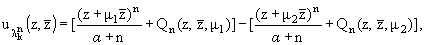 |
(17) |
где
Теорема 1. Функции u, построенные
согласно формулам (17), являются системой полиномиальных собственных функций
краевой задачи (5), (6), соответствующих собственным значениям
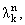 k = 1, 2, ..., (n - 1), n = 2, 3, ..., каждое из которых имеет бесконечную
кратность.
k = 1, 2, ..., (n - 1), n = 2, 3, ..., каждое из которых имеет бесконечную
кратность.
Доказательство. Функция
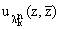 представляет собой сумму двух слагаемых, отмеченных
квадратными скобками в формуле (17), первое из которых является функцией от
представляет собой сумму двух слагаемых, отмеченных
квадратными скобками в формуле (17), первое из которых является функцией от
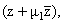 второе
- функцией от
второе
- функцией от
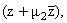 и поэтому она удовлетворяет уравнению (5). Покажем, что
функции
и поэтому она удовлетворяет уравнению (5). Покажем, что
функции
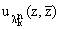 удовлетворяют граничному условию (6). В самом деле, на
основании леммы 2 и формулы (15) имеем
удовлетворяют граничному условию (6). В самом деле, на
основании леммы 2 и формулы (15) имеем
Собственные значения краевой задачи (5), (6) являются бесконечно
кратными. Этот факт следует из того, что
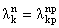 при любом натуральном P и что
собственные функции
при любом натуральном P и что
собственные функции
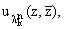 соответствующие собственному значению
соответствующие собственному значению
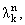 как полиномы различных порядков
линейно независимы. Теорема доказана.
как полиномы различных порядков
линейно независимы. Теорема доказана.
Теорема 2. Совокупность полиномиальных собственных
функций (17) задач (5), (6) образует двукратно полную систему в гильбертовом
пространстве
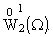
Доказательство. Известно, что система векторов
|
м
н
о |
Vln = |
ж
з
и |
Vln
ln · Vln
|
ц
ч
ш |
|
ь
э
ю |
Ґ
n =
1
|
| |
(19) |
образует полную систему в ортогональной сумме гильбертовых пространств
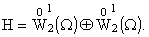 Так как
Так как
положим
|
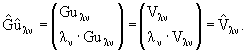 |
(21) |
Пусть
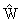 О H - произвольная вектор-функция с
полиномиальными компонентами
О H - произвольная вектор-функция с
полиномиальными компонентами
|
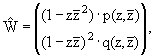 |
(22) |
где p и q произвольные полиномы от
z и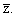 Тогда очевидно, что
Тогда очевидно, что
 О H. Но, как показано в [4], вектор-функцию
О H. Но, как показано в [4], вектор-функцию
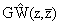 можно представить в виде конечной комбинации собственных
векторов Vln
можно представить в виде конечной комбинации собственных
векторов Vln
|
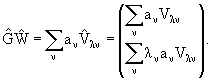 |
(23) |
Из
(21) и (18) имеем
|
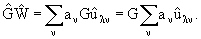 |
(24) |
В
силу существования обратного оператора G-1
из (23) заключаем
|
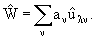
|
(25) |
Но
поскольку, как это показано в работе [4], множество полиномиальных векторов вида
(22) всюду плотно в гильбертовом пространстве H, то теорема
доказана.
Отметим, что полученные нами
собственные значения расположены всюду плотно на кривой |4l2 + 1| = 1 в комплексной плоскости. Ясно, что для всякого
собственного значения задачи Дирихле существуют собственные функции, которые
исчезают в начале координат. Таким образом, в случае a
> 0 каждой собственной функции задачи Дирихле соответствует одна собственная
функция (5), (6).
Рассуждая аналогично, легко
получить собственные функции уравнения
если L,N,M - линейные
дифференциальные операторы второго порядка с постоянными коэффициентами,
содержащие лишь вторые производные по x и y, причем тип уравнения (26) не играет
роли.
Замечание. В
случае a = 0, т.е. задачи Неймана, оператор G принимает
вид
|
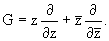 |
(27) |
Этот оператор в пространстве всех полиномов не имеет обратного
G-1. Очевидно, что если задача Неймана имеет
решение для некоторого l, то соответствующее этому
решению решение задачи Дирихле удовлетворяет условию u(0,0) = 0. В этом случае
оператор G-1 можно применить на тех
полиномах, которые обращаются в нуль в начале координат. Здесь уже те функции из
систем
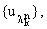 которые
не исчезают в центре координат, не пригодны для наших целей. Таким образом,
система полиномиальных собственных функций задачи Неймана не образует двукратно
полную систему в гильбертовом пространстве
которые
не исчезают в центре координат, не пригодны для наших целей. Таким образом,
система полиномиальных собственных функций задачи Неймана не образует двукратно
полную систему в гильбертовом пространстве
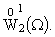 Если a > 0, то
построенная совокупность полиномиальных собственных функций образует полную
систему в Если a > 0, то
построенная совокупность полиномиальных собственных функций образует полную
систему в
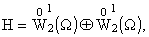 а при a = 0 (задача
Неймана) полнота нарушается. а при a = 0 (задача
Неймана) полнота нарушается.
Военный авиационный институт им. маршала А.
Ханферянца
Литература
1. Зеленяк Т. И. - ДАН СССР.
1964. Т. 158. №6. C. 1268-1270.
2. Саргсян
Г. А. - Уч. зап. ЕГУ. 1994. №1 (180). C. 19-25.
3. Крейн М. Г., Лангер Г. К. - Тр. Междунар. симп. по применению т.ф.к.п. в механике сплошной среды. М.
Наука. 1965.
4. Вирабян Г. В. - ДАН АрмСССР. 1969. Т. 48. №2. C. 65-70.
| ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() является двукратно полной в смысле М. В. Келдыша
[3]. Перейдем теперь к решению задачи (5), (6). Она состоит в нахождении функций
из класса C2(W) И C1(W), удовлетворяющих
уравнению (5) в круге
является двукратно полной в смысле М. В. Келдыша
[3]. Перейдем теперь к решению задачи (5), (6). Она состоит в нахождении функций
из класса C2(W) И C1(W), удовлетворяющих
уравнению (5) в круге
![]() и граничным условиям (6) на границе
и граничным условиям (6) на границе
![]()
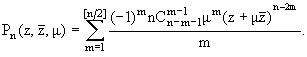
![]() m), которые используются в
дальнейшем.
m), которые используются в
дальнейшем.![]() m) при n = 2, 3, ... удовлетворяют рекуррентному
соотношению
m) при n = 2, 3, ... удовлетворяют рекуррентному
соотношению![]()
![]() m) на
окружности круга W удовлетворяют рекуррентному
соотношению
m) на
окружности круга W удовлетворяют рекуррентному
соотношению ![]()
![]()
![]() m) = Pn(z,
m) = Pn(z,![]() m),
m),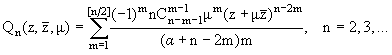
![]()
![]()
![]() k = 1, 2, ..., (n - 1), n = 2, 3, ..., каждое из которых имеет бесконечную
кратность.
k = 1, 2, ..., (n - 1), n = 2, 3, ..., каждое из которых имеет бесконечную
кратность.![]() представляет собой сумму двух слагаемых, отмеченных
квадратными скобками в формуле (17), первое из которых является функцией от
представляет собой сумму двух слагаемых, отмеченных
квадратными скобками в формуле (17), первое из которых является функцией от
![]() второе
- функцией от
второе
- функцией от
![]() и поэтому она удовлетворяет уравнению (5). Покажем, что
функции
и поэтому она удовлетворяет уравнению (5). Покажем, что
функции
![]() удовлетворяют граничному условию (6). В самом деле, на
основании леммы 2 и формулы (15) имеем
удовлетворяют граничному условию (6). В самом деле, на
основании леммы 2 и формулы (15) имеем ![]()
![]()
![]()
![]() при любом натуральном P и что
собственные функции
при любом натуральном P и что
собственные функции
![]() соответствующие собственному значению
соответствующие собственному значению
![]() как полиномы различных порядков
линейно независимы. Теорема доказана.
как полиномы различных порядков
линейно независимы. Теорема доказана.![]()
![]() Так как
Так как 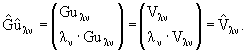
![]() О H - произвольная вектор-функция с
полиномиальными компонентами
О H - произвольная вектор-функция с
полиномиальными компонентами
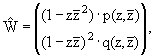
![]() Тогда очевидно, что
Тогда очевидно, что
![]() О H. Но, как показано в [4], вектор-функцию
О H. Но, как показано в [4], вектор-функцию
![]() можно представить в виде конечной комбинации собственных
векторов Vln
можно представить в виде конечной комбинации собственных
векторов Vln
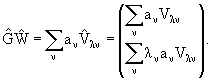
![]()
![]()
![]()
![]() которые
не исчезают в центре координат, не пригодны для наших целей. Таким образом,
система полиномиальных собственных функций задачи Неймана не образует двукратно
полную систему в гильбертовом пространстве
которые
не исчезают в центре координат, не пригодны для наших целей. Таким образом,
система полиномиальных собственных функций задачи Неймана не образует двукратно
полную систему в гильбертовом пространстве