ФИЗИЧЕСКАЯ ХИМИЯ
УДК 541.124.7.519.6
Руб. Т. Малхасян, Ш. Р. Эксузян, академик И. А. Варданян
Исследование влияния гетерогенных радикальных стадий на
осцилляционный режим окисления метана методом
математического
моделирования
(Представлено 25/IV 2006)
Ключевые слова: метан, окисление, моделирование, поверхность, радикал
Сравнительно недавно появились убедительные
доказательства наличия в процессе термического окисления метана осцилляций,
сопровождающиxся свечением [1]. Однако механизм их появления неясен. В последнее
время все больше внимания уделяется участию гетерогенных радикальных стадий в
цепных радикальных реакциях газофазного окисления органических соединений [2-6].
В этом ряду метан, который является экологически более чистым топливом, занимает
особое место.
В настоящей работе поставлена
задача исследовать роль гетерогенных радикальных стадий в возбуждении
осцилляционных режимов окисления метана в проточных условиях. На основании
анализа схемы окисления метана, представленной в работе [7], выделена краткая
модель, включающая основные стадии цепного радикального процесса.
CH3+O2 ®
CH3O2 1. CH3O2+CH2O ®
CH3OOH+HCO 6.
CH3O2 ®
CH3+O2 1ў. CH3O+CH4 ® CH3OH +CH3
7.
CH3O2+CH4 ® CH3OOH+CH3
2. CH2O+M ® продукт 8.
CH3OOH
 OH+CH3O 3. CH3O2 OH+CH3O 3. CH3O2 |  s s | гибель 9.
OH+CH4 ®
CH3+H2O 4. H ® продукт 10.
CH3O ®
CH2O+H 5. HCO ® HO2 ® гибель 11.
CH3O+O2 ® CH2O+HO2
5a.
где S - поверхность реактора и M - частица.
Осцилляционный режим реакции возможен при наличии отрицательной обратной
связи. Эту роль в схеме выполняет стадия 6, поскольку радикал HCO быстро
переходит в менее активный радикал HO2. На основании имеющихся данных
[2-6] принимается, что стадии 6 и 9 протекают на поверхности реактора. Гибель
пероксидных радикалов CH3O2 рассматривается с учетом
заполнения поверхности и ее скорость имеет вид, характерный для гетерогенных
процессов: W9 = A[CH3O2]/(1 + a[CH3O2]) ([8], c. 532-568), где A и a - параметры.
На
основании представленной модели были написаны соответствующие дифференциальные
уравнения для изменений концентраций реагентов. Система решалась в
квазистационарном приближении для концентраций радикалов OH, CH3O,
CH3 на начальной стадии реакции, когда пренебрегается расходованием
метана и кислорода. В конечном счете система дифференциальных уравнений сводится
к двум:
| d[CH3O2]/dt = K2ў[CH3O2] - k6ў[CH3O2][CH2O] - A[CH3O2]/(1 + a[CH3O2]), | |
(1) |
| d[CH2O]/dt = K2ў[CH3O2] - k6ў[CH3O2][CH2O] - K8[CH2O]. | |
(2) | Введя следующие обозначения:
| [CH3O2] = X, [CH2O] = Y, K2 = k2[CH4], K1 = k1[O2],
| |
| K2ў = mK2, k6ў = k6(1 - m), | |
| m = k
3[CH3OOH]/(K2 + k2[CH2O])[CH3O2], 0
< m < 1, | | систему (1) и
(2) можно записать следующим образом:
| dX/dt = Kў2X -
kў6XY - AX/(1 + aX),
| |
(1ў) |
| dY/dt = Kў2X - kў6XY - K8Y. | |
(2ў) |
Как видно
из полученных выражений, в принятых приближениях практически важную роль играют
стадии 2, 3, 6, 8, 9.
Для выяснения
возможности колебательного режима в системе использовался математический
аппарат, предложенный в [9] и развитый в [8]. Наличие колебательного режима
определяется существованием особой точки типа фокуса. В случае устойчивого
фокуса возможны затухающие колебания, а в случае неустойчивого фокуса -
самораскачивающиеся. Автоколебательный режим возможен, когда при наличии
неустойчивого фокуса наблюдается предельный цикл - замкнутая кривая, на которую
наматываются фазовые траектории системы.
Для
анализа были выбраны начальные условия работы [1], в которой наблюдались
осцилляции: [CH4] = 4.7 × 1017 молек./см3,
[O2] = 2.3 × 1017 молек./см3, T = 825 K. В этих
условиях K2 = 350 с-1. Что касается
значений констант гетерогенных радикальных стадий, то они носили несколько
произвольный характер, однако были в рамках допустимых значений
[7].
Был проведен анализ особых точек системы
дифференциальных уравнений (1) и (2), который показал, что в зависимости от
величин констант скорости гетерогенных стадий и значений параметров возможно
существование устойчивого и неустойчивого фокусов.
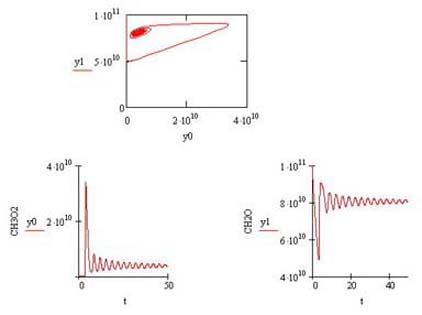
На рис.1 приведены фазовый портрет системы и изменения концентраций
радикалов и формальдегида в зависимости от времени (с). При указанных значениях
параметров имеет место устойчивый фокус и, как и следовало ожидать, наблюдаются
затухающие колебания.
|
|
Рис. 1. Фазовый портрет системы и изменения концентрации
радикалов CH3O2 и CH2O в
зависимости от
времени. Kў2=35 с-1, kў6=3.8×10-10
cм3молек.-1 с-1, K8=0.207 с-1,
A=6.9 с-1,
a = 1.5×10-10
cм3 част.-1, m=0.1.
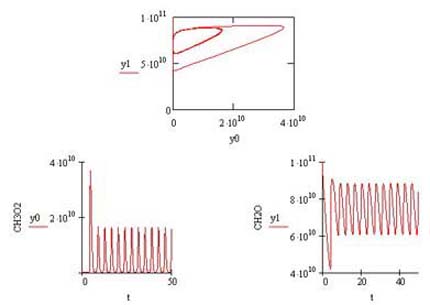
Предельные циклы - замкнутые
кривые, на которые наматываются фазовые траектории системы, имели место при
значении параметра A = 8.9. При этом наблюдается увеличение амплитуды осцилляций.
Фазовый портрет системы в этом случае представлен на рис 2. Как видно из
рисунка, в системе происходят автоколебания.
Вариации параметров в варианте, представленном на рис. 2, дали следующие
результаты. Уменьшение a до 8 × 10-11 cм3 част.-1 и его увеличение до 3.2 × 10-10 cм3 част.-1 приводит к затуханию колебаний. a = 3.1 × 10-10
cм3 част.-1 является предельным
значением, ниже которого имеют место автоколебания, а выше - затухающие
колебания. B варианте, представленном на рис. 1, при изменении kў6 до 2.8 имеет место затухание, а при 1.8
колебаний нет. Уменьшение K8 приводит к появлению
автоколебаний.
Свечение в процессах окисления
органических соединений обычно приписывается рекомбинации радикалов. В
колебательном режиме окисления метана концентрационные колебания радикалов
естественно вызовут колебания интенсивности свечения.
|
|
Рис. 2. Фазовый портрет системы и изменения концентрации
радикалов CH3O2 и CH2O в
зависимости от
времени. Kў2=35 с-1, kў6=3.8×10-10
cм3молек.-1 с-1, K8=0.207 с-1,
A=8.9 с-1,
a = 1.5×10-10
cм3 част.-1, m=0.1.
Обобщая полученные расчетным
путем результаты, можно заключить, что изменение природы поверхности
реакционного сосуда, находящее в данном случае отражение в изменении констант
скоростей гетерогенных радикальных стадий, влияет на характер динамического
режима.
Институт химической физики им. А. Б.
Налбандяна НАН РА
Литература
1. Vanpee M. In: Intern. Conf.
On Combustion Technology for a Clean Environment. Lisboa. 1991. P. 779 -790.
2. Bakhchadjyan R. H., Vardanyan I. A. -
Intern. J. Chem. Kinetics. 1994. V. 26. P. 595-603.
3. Keheyan E. M., Vardanyan I. A. - Arm. Chim. Jour. 1998. V. 51. P. 177-181.
4. Sargsyan G. S., Yessayan R. S., Vardanyan I. A. - J.
Appl. Catalysis A. 2000. V. 203. P. 285-291.
5. Манучарова Л. А., Царукян С. В., Варданян И. А. - ДHАН
Армении. 2003. Т. 103. № 2. C. 121-125.
6.
Manucharova L. A., Tsarukyan S. V., Vardanyan I. A. - Intern. J.
Chem. Kinetics. 2004. V. 36. P. 591-595.
7.
Vardanyan I. A., Nalbandyan A. B. - Intern. J. Chem. Kinetics.
1985. V. 17. P. 901-924.
8. Грей П., Скотт
С. Колебания и бегущие волны в химических системах. М. Мир. 1988.
720 с.
9. Франк-Каменецкий Д. А. - Диффузия и теплопередача в химической кинетике. М. Наука. 1967. 492 c.
|