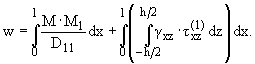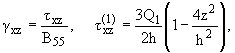Reports-2006-Vol106-N3-Kirakosyan

МЕХАНИКА

УДК 531.8

Р. М. Киракосян

О поправочных коэффициентах, учитывающих влияние
распределения касательных напряжений по толщине пластинки

(Представлено академиком С. А. Амбарцумяном 5/VI 2006)

Ключевые слова: поправочные коэффициенты, касательные поверхностные нагрузки, пластинка, сдвиг, линейный

Показано, что если теория пластин строится на основе гипотез только для перемещений, то существуют поправочные коэффициенты k_x, k_y, учитывающие влияние распределения касательных напряжений t_xz, t_yz по толщине пластинки. Если же теория пластин опирается на гипотезы для касательных напряжений t_xz, t_yz (например [1]), то законы распределения этих напряжений непосредственно участвуют в построении теории и необходимость введения поправочных коэффициентов автоматически отпадает.
1. Гипотезы теории [2] ,,… отличаются от современной формы гипотез Кирхгофа только тем, что не требуют ортогональности нормального элемента пластинки к ее изогнутой срединной плоскости…’’ При построении этой теории считается, что нормальные элементы пластинки недеформируемы, в силу чего их поведение не зависит от закона распределения касательных напряжений t_xz, t_yz по толщине пластинки и определяется только их равнодействующими, т.е. поперечными, силами Q_x, Q_y. Это приводит к утверждению о том, что поправочные коэффициенты, традиционно вводимые для учета влияния распределения напряжений t_xz, t_yz по толщине пластинки, существовать не могут. Отметим, что недеформируемость нормальных элементов аргументируется только тем, что согласно принятым гипотезам длина этих элементов при изгибе пластинки не изменяется. Причем это отождествляется с игнорированием деформации e_z. Однако согласно закону Гука даже в случае материалов, имеющих лишь одну плоскость упругой симметрии, параллельную срединной плоскости пластинки, деформация e_z не зависит от касательных напряжений t_xz и t_yz [1]. В силу этого игнорирование e_z не может быть основанием для неучета влияния распределения этих напряжений по толщине пластинки. Кроме того, если считается, что перемещение

u_z(x,y,z) = w(x,y) + z
у
х
0
e_zdz,
(1.1)

нормальное к срединной плоскости, по толщине пластинки не изменяется, то игнорируется не сама деформация e_z, а ее интеграл по z. Этот интеграл мал из-за малости не e_z, а промежутка интегрирования, поскольку |z| Ј h/2, а толщина пластинки h намного меньше ее планарных размеров.
Покажем, что e_z может быть по модулю больше деформаций e_x и e_y. С этой целью рассмотрим изотропную квадратную пластинку постоянной толщины, которая при одинаковых условиях по всему контуру несет равномерно распределенную поперечную нагрузку. Во всех точках диагональных сечений пластинки y = ±x, которые симметрично расположены относительно оси z, имеет место равенство

e_x= e_y.

(1.2)

При несжимаемости материала

e_x+ e_y+ e_z= 0 Ю e_z= -2e_x= -2e_y,

(1.3)

т.е. в отмеченных точках, e_z в два раза по модулю больше e_x и e_y. Однако и в этом случае допущение о неизменности перемещения u_z по толщине пластинки вполне приемлемо. Конечно, реальные материалы не являются идеально несжимаемыми. Но тогда e_z будет больше e_x и e_y не в два раза, а, скажем, в полтора, т.е. будет снова неигнорируемой.
Дополнительно отметим, что если в теории пластин на самом деле считать e_z= 0, то можно будет определить напряжение s_z непосредственно из закона Гука. Для изотропных пластин это приведет к выражению

s_z= n(s_x+ s_y),

(1.4)

что не соответствует действительности. (Здесь n - коэффициент Пуассона материала). Поэтому s_z определяют интегрированием третьего дифференциального уравнения равновесия сплошной среды с использованием условий на поверхностях пластинки.
   Разумеется, только неизменность длины нормальных элементов недостаточна для того, чтобы считать их недеформируемыми - это может быть, например, следствием знакопеременности e_z по толщине пластинки. А то, что после изгиба первоначально нормальные элементы пластинки больше не перпендикулярны к ее срединной поверхности, свидетельствует об изменении прямых углов, т.е. о наличии деформаций поперечных сдвигов. Следовательно, нормальные элементы деформируемы, как минимум, в смысле поперечных сдвигов.
   При построении теории [2] искривленные от неоднородных поперечных сдвигов первоначально нормальные элементы просто аппроксимируются прямыми элементами, которые не перпендикулярны к срединной поверхности изогнутой пластинки. Углы наклона аппроксимирующих прямых элементов как раз и зависят от формы распределения касательных напряжений t_xz, t_yz по толщине пластинки. Следовательно, нормальные элементы деформируемы, в силу чего поправочные коэффициенты, традиционно вводимые для учета влияния распределения t_xz, t_yz по толщине пластинки ([3-5] и др.), существуют. Вопрос в другом - учитывать это обстоятельство или нет?
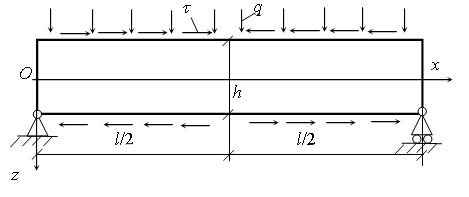
   2. Рассмотрим пластинку-полосу постоянной толщины h и ширины l. Координатную плоскость xoy совместим со срединной плоскостью. Ось oy направим вдоль одной из длинных сторон, ось oz - вертикально вниз. Пусть поверхностные нагрузки и условия на краях таковы, что все расчетные величины пластинки-полосы не зависят от координаты y.
   Будем считать, что нормальные элементы пластинки-полосы после деформирования остаются прямолинейными. Это влечет за собой линейное распределение напряжений s_x, s_y и t_xy по толщине. Тогда согласно первому дифференциальному уравнению равновесия сплошной среды касательное напряжение t_xz вдоль толщины пластинки-полосы будет изменяться по закону квадратной параболы. Имея в виду это обстоятельство и удовлетворяя условиям на поверхностях z = ±h/2, получим

t_xz=

ж
з
и

1 -

4z²

h²

ц
ч
ш

X₁

ж
з
и

1 -

12z²

h²

ц
ч
ш

X₂.

(2.1)

Здесь Q - поперечная сила,

X₁=

X⁺ - X^-

, X₂= X⁺+ X^-.

(2.2)

Через X^± обозначены проекции интенсивностей поверхностных нагрузок на ось x. Знаки ,,+’’ и ,,-’’ относятся к поверхностям z = +h/2 и z = -h/2 соответственно.
Пользуясь принципом возможной работы и методом единичной силы, для прогиба некоторой точки пластинки-полосы w можно написать [4]

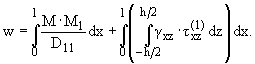
(2.3)

Здесь D₁₁ - цилиндрическая жесткость на изгиб, M и g_xz - изгибающий момент и деформация поперечного сдвига от реально действующих нагрузок, M₁ и 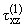- изгибающий момент и касательное напряжение от той единичной силы, которую следует представить нормально приложенной в той точке пластинки-полосы, для которой определяется прогиб.
Очевидно, что

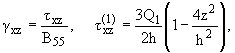
(2.4)

где B₅₅ - модуль сдвига материала в плоскости xoz, Q₁ - поперечная сила от единичной силы.
С учетом (2.1) и (2.4) выражение (2.3) можно представить в виде

w =

l
у
х
0

M · M₁

D₁₁

dx +

l
у
х
0

kQQ₁

B₅₅h

dx, k =

X₁h

(2.5)

гдe k - поправочный коэффициент, учитывающий влияние распределения касательного напряжения t_xz по толщине пластинки-полосы. Отрицать существование этого коэффициента равносильно отрицанию принципа возможной работы, метода единичной силы и неравномерности распределения напряжения t_xz по толщине пластинки.
Заметим, что выражение (2.6) означает линейную зависимость между значениями поперечной силы Q и приведенного поперечного сдвига сечения пластинки-полосы g:

g =

B₅₅h

X₁

5B₅₅

, Q =

B₅₅hg +

X₁h

(2.6)

3. Рассмотрим пример. Пусть на пластинку-полосу, шарнирно опертую вдоль длинных сторон, совместно действуют равномерно распределенная нормальная и по линейному закону переменно распределенные касательные поверхностные нагрузки (рисунок):

q = const, X⁺= -t(l - 2x), X^-= t(l - 2x), (X₁= -t(l - 2x), X₂= 0).

(3.1)

Не вдаваясь в подробности, приведем выражения прогиба и его максимального значения по теориям [2] и [1]:
а) по теории [2]

w =

q + 2th

24D₁₁

x(l³ - 2lx²+ x³) +

2B₅₅h

x(l - x),

(3.2)

w_max= w|_x=[l/2]=

5(q + 2th)

384D₁₁

l⁴

ж
з
и

1 +

q + 2th

B₁₁

B₅₅

h²

l²

ц
ч
ш

;

(3.3)

б) по теории [1]

w = q + 2th
24D₁₁
x(l³ - 2lx²+ x³) + 3q + th
5B₅₅h
x(l - x),
(3.4)

w_max= w|_x=[l/2]= 5(q + 2th)
384D₁₁
l⁴ ж
з
и 1 + 8
25
3q + th
q + 2th
B₁₁
B₅₅
h²
l²
ц
ч
ш .
(3.5)

   Напомним, что теория [2] не учитывает влияние распределения напряжения t_xz по толщине пластинки, а теория [1] это влияние учитывает.
   Интересно отметить, что результаты теории [1] совпадают с соответствующими результатами, полученными по принципу виртуальной работы и методу единичной силы [4].
   Внутри скобок формул максимального прогиба число ,,1’’ относится к теории Кирхгофа, а вторые слагаемые - к поправкам. Поправку, полученную с учетом влияния распределения напряжения t_xz по толщине пластинки-полосы, обозначим через D_k, а без его учета - через D. Отношение этих поправок составляет

D_k

l
у
х
0

kdx.

(3.6)

Из (2.1) видно, что при совместном действии нормальной и касательных нагрузок касательное напряжение t_xz состоит из трех слагаемых. К задаче изгиба относятся первые два слагаемые. Они имеют квадратичные распределения по толщине. Очевидно, что влияние деформации поперечного сдвига - это суммарное влияние этих двух слагаемых. Первое из них прямо пропорционально поперечной силе Q, а второе - параметру касательных поверхностных нагрузок X₁. Первое слагаемое является знакопостоянной функцией поперечной координаты z и его интеграл по толщине пластинки-полосы равен поперечной силе Q. Второе же слагаемое знакопеременное и его интеграл по толщине равен нулю. Несмотря на это вклад второго слагаемого в значение прогибов пластинки-полосы все же отличен от нуля. В рассмотренном примере этот вклад для максиального прогиба составляет

l
у
х
0

h/2
у
х
-h/2

й
к
л

3Q₁

2B₅₅h

ж
з
и

1 -

4z²

h²

ц
ч
ш

X₁

ж
з
и

1 -

12z²

h²

ц
ч
ш

щ
ъ
ы

dz =

tl²

20B₅₅

(3.7)

В таблице представлены значения поправок и их отношения для некоторых видов нагрузок.

	D_k	D	D_k/D
q № 0, t = 0	[24/25][(B₁₁)/(B₅₅)][(h²)/(l²)]	[4/5][(B₁₁)/(B₅₅)][(h²)/(l²)]	[6/5]
q = 0, t № 0	[4/25][(B₁₁)/(B₅₅)][(h²)/(l²)]	0	-
[q/(th)] = a	[8/25][(3a+1)/(a+2)][(B₁₁)/(B₅₅)][(h²)/(l²)]	[4/5][(a)/(a+2)][(B₁₁)/(B₅₅)][(h²)/(l²)]	[6/5]+[2/(5a)]

Таким образом, влияние деформации поперечного сдвига обусловлено четырьмя факторами: величинами Q,X₁ и формами распределения соответствующих слагаемых касательного напряжения. В рассмотренном примере теория [2] из этих четырех факторов учитывает только один - величину поперечной силы. Поэтому теорию [2] следует назвать теорией, учитывающей влияние не деформаций поперечных сдвигов, а только поперечных сил. В случае отсутствия поперечных сил результаты теории [2] будут совпадать с соответствующими классическими результатами. Такая ситуация имеет место в рассмотренном примере, когда на пластинку-полосу действуют только касательные поверхностные силы (q = 0, t № 0). В этом случае поперечная сила Q всюду равна нулю и, как видно из таблицы, поправка теории [2] отсутствует (D = 0). В отличие от этого теория [1], а также принцип возможной работы и метод единичной силы, при которых учитываются влияния всех четырех вышеотмеченных факторов, для этого же случая дают поправку

D_k=

B₁₁

B₅₅

h²

l²

(3.8)

Для толстых пластин-полос, изготовленных из современных анизотропных материалов, эта поправка может оказаться существенной. Например, при h/l = 1/5 и B₁₁/B₅₅= 40 [1]

D_k= 25.6%.

(3.9)

Институт механики НАН РА

Литература

    1. Амбарцумян С. А. Теория анизотропных пластин. М. Наука. 1987. 360 с.
    2. Васильев В. В. - Изв. АН МТТ. 1998. №3. C. 46-58.
    3. Reissner E. - Trans. ASME. 1945. V. 67. P. A69-A77.
    4. Тимошенко С.П., Гере Дж. Механика материалов. M. Миp. 1976. 669 с.
    5. Григоренко Я. М., Василенко А. Т. Теория оболочек переменной жесткости. Киев. Наукова думка. 1981. 544 с.