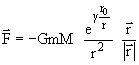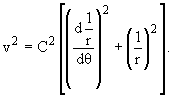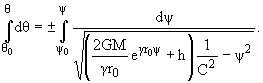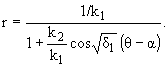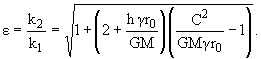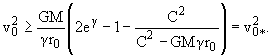УДК 531.5

   Ключевые слова: центральное взаимодействие, тяготение, силовое поле, орбита

   Построенная в средние века теория движения солнечной планетной системы явилась триумфом науки, в частности, механики. Длившееся веками противостояние между сторонниками птолемеевой геоцентрической системы и гелиоцентрической системы Аристарха - Коперника завершилось победой последних. Спустя восемнадцать веков после Аристарха Коперник в ХVI в. возродил гелиоцентрическую модель, а в начале следующего столетия Кеплер, используя составленный Тихо Браге великолепный каталог наблюдений по движению планет, сформулировал свои знаменитые три закона о движении планет. Несколько десятилетий спустя Ньютон математически обосновал законы Кеплера и сформулировал закон всемирного тяготения. Согласно закону Ньютона сила всемирного тяготения центральная, каждая масса m притягивается другой массой M во Вселенной с силой, обратно пропорциональной квадрату расстояния между массами и направленной по линии, соединяющей центры масс. Различные варианты центральных сил, при которых решение уравнения движения приводится к квадратурам, рассмотрены Якоби, Бертраном, Дарбу, Альфеном. Однако ими не было описано хоть одно реально существующее движение [1,2].
   В XIX в. было обнаружено некоторое расхождение расчетной орбиты ближайшей к Солнцу планеты Меркурий в перигее с результатами наблюдений. Не найдя убедительных объяснений этого факта, Симон Ньюкомб в 1895 г. высказал мнение, что, возможно, закон обратных квадратов Ньютона не выполняется точно на малых расстояниях. В 1917 г. факту, связанному с орбитой Меркурия, было дано объяснение на основе общей теории относительности (ОТО) Эйнштейна и противоречие казалось исчерпанным. В 1966 г. Р. Дикке и М. Голденбергом в результате тонкoго экспериментa было доказано, что Солнце не является шарообразным и eго полярный диаметр на 35 км меньше, чем экваториальный, что позволяло объяснить остаточноe смещениe перигелия Меркурия примерно на 10%. Это ставило под сомнение уже согласие ОТО с результатами наблюдений [2,3].
   Другая особенность создавшегося положения связана с вопросом существования «черных дыр». В 1783 г. английский астроном-любитель, один из основателей сейсмологии Джон Митчелл, а в 1798 г. известный французский математик и механик Лаплас независимо друг от друга, основываясь на использовании закона тяготения Ньютона, высказали мнение, что в природе должны существовать тела, для которых необходимая для преодоления их притяжения скорость превышает скорость света. Поэтому такие тела должны быть темными (по современной терминологии «черные дыры»). Подобные тела невидимы и их можно обнаружить косвенным путем - гравитационным воздействием на другие тела. Митчелл и Лаплас вывели радиус темного тела r_g (гравитационный радиус) при заданной его массе, используя понятие второй космической скорости (r_g = 2GM/c²). После построения ОТО рассуждения Митчелла и Лапласа подверглись критике в том плане, что при близких к скорости света скоростях формулы классической механики не применимы, хотя по обeим теориям получается одно и то же значение для гравитационного радиуса. Оппоненты же ОТО утверждают, что она не применима, поскольку решение уравнений этой теории содержит особенность (сингулярность), недопустимyю при описаниях естественных явлений.
   Приведенные выше факты обуслoвливают актуальность затронутого Ньюкомбом вопроса, а именно: существует ли такое центральное взаимодействие, которое при малых расстояниях отличается от ньютоновского, а при больших - совпадает с ним. Ниже дается положительный ответ на поставленный вопрос.
   1. Рассмотрим вариант центрального взаимодействия тел, который является универсальным - при коротких расстояниях описывает сильное, по сравнению с ньютоновым гравитационным, взаимодействие, а при сравнительно больших расстояниях практически совпадает с классическим гравитационным (ньютоновым) взаимодействием. Пусть имеем тела (частицы) с массами m,M. Поместив начало координат в центре тела массoй M, центральную силу взаимодействия будем задавать в виде

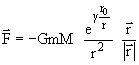
(1.1)

или

F = -GmM eg[(r0)/r] r2 ,

(1.2)

где G - гравитационная постоянная в законе всемирного тяготения, 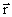- радиус-вектор материальной точки массы m,r₀ - некоторый характерный размер (начальное расстояние от центра притяжения, гравитационный радиус и др.), g- неотрицательный, безразмерный параметр (g і 0). Если r >> r₀, то F, вычисленный по формуле (1.2), практически совпадает (при g = 0 точно) с F в законе всемирного тяготения:

F = -G mM r2 ;

(1.3)

если же r << r₀, доминирующую роль будет играть exp(gr₀/r), т.е. будем иметь более сильное, чем ньютоново, гравитационное взаимодействие. Параметр g будет характеризовать мощность (интенсивность) центра притяжения. Поле, создаваемое силой 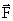, задаваемой по формуле (1.1), является потенциальным с потенциалом

U = - GmM gr0 e[(gr0)/r] + const.

(1.4)

   Поскольку сила 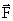центральная, имеет место закон площадей:

r2 dq dt = C,

(1.5)

траектория материальной точки - плоская кривая, C равна величине момента начальной скорости относительно центра притяжения. Скорость точки в полярной системе координат (r,q) с учетом (1.5) вычисляется по формуле

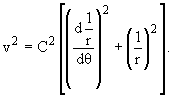
(1.6)

   Применив теорему о кинетической энергии ([(dmv²)/2] = Fdr), получим

v2 = 2GM gr0 e[(gr0)/r] + h;

(1.7)

постоянная интегрирования h определяется из начального условия. Если при r = r₀ v = v₀,

h = v 02 - 2GM gr0 eg.

(1.8)

   Обозначив y = 1/r, из (1.6), (1.7) следует

ж з и dy dq ц ч ш 2   = ж з и 2GM gr0 egr0y + h ц ч ш 1 C2 - y2.

(1.9)

   Определение траектории движения в общем случае приводится к вычислению интеграла

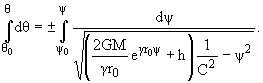
(1.10)

   Чтобы выяснить форму траектории, разложим exp(gr₀y) в ряд Маклорена и ограничимся первыми тремя слагаемыми

egr0y » 1 + gr0y + 1 2 (gr0)2y2,

(1.11)

тогда (1.9) примет вид

ж з и dy dq ц ч ш 2   = d1 й к л - (y - k1)2 + k22 щ ъ ы ,

(1.12)

где

d1 = 1 - MGgr0 C2 ,    k1 = MG C2d1 ,

(1.13)

k22 = 1 C2d12 [MG + (MG + hgr0)d1] 1 gr0 ,

будем считать d₁ > 0, тaк кaк лишь при этом получится периодическое решение, а траектория будет коническим сечением. Обозначив y - k₁ = k₂r, уравнение (1.12) примет вид

ж з и dr dq ц ч ш 2   = d1(1 - r2),

(1.14)

решением которого является

r = cos Ц   d1   (q - a).

(1.15)

Вернувшись к исходным обозначениям, получим

y = k1 + k2cos Ц   d1   (q - a),

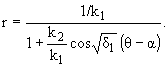
(1.16)

Tаким образом, траектория движения есть коническое сечение с параметрами

p = 1 k1 = C2 GM - gr0,

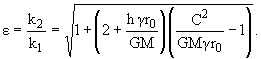
(1.17)

   В силу d₁ > 0 имеем (C²/GMgr₀) - 1 > 0, поэтому e < 1 лишь при 2 + (hgr₀/GM) < 0 или

h < -2GM gr0 .

(1.18)

Используя (1.8), из (1.18) получим

v02 < 2GM r0 eg - 1 g = v*2.

(1.19)

Tаким образом, при v₀ < v_* траектория есть эллипс, при v₀ = v_* - парабола, а при v₀ > v_* - гипербола. Одновременно из условия e і 0 следует

h і - GM gr0 ж з и 1 + C2 C2 - GMgr0 ц ч ш

или

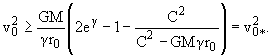
(1.20)

   Итак, при v_0* < v₀ < v_* траектория есть эллипс, полуоси которого

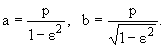
(1.21)

   Сохранение в ряде Маклорена функции exp(gr₀y) больше слагаемых, чем в (1.11), приводит к вычислению эллиптических интегралов и незначительным поправкам к параметрам траектории.
   При g ® 0 v_*² ® 2GM/r₀, что, как следовало ожидать, совпадает с известной скоростью (вторая космическая скорость) по теории Ньютона. Если g № 0, v_*² >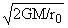, т.е. вторая космическая скорость при взаимодействии (1.1) больше классической.
   2. Поставим вопрос: при заданной массе M тела каков должен быть его радиус (R_g), чтобы онo было невидимым («черной дырой»). Это означает, что любое тело (частица) массой m с начальной скоростью, даже равной скорости света c, не может преодолеть поле притяжения тела массoй M. Исходя из этого, приняв в формуле (1.19) r₀ = R_g, v_* = c, получим

2GM Rg eg - 1 g = c2.

(2.1)

   Отсюда следует

Rg = 2GM c2 eg - 1 g

(2.2)

или

Rg = rg eg - 1 g ,

(2.3)

где r_g = (2GM/c²) - известный гравитационный радиус, полученный и по теории Ньютона, и по теории ОТО. При r₀ < R_g любая частица (тело) не может преодолеть гравитационное поле тела массoй M. Если g ® 0, то R_g ® r_g. Из (2.2) одновременно следует, что при g № 0, R_g > r_g, т.е. теоретически могут существовать тела со сколь угодно большим гравитационным радиусом. При заданной массе M чем больше g, тем больше гравитационный радиус. Мы здесь не останавливаемся на способах определения g, это предмет отдельного обсуждения. Yкажем лишь, что, если каким-либо способом оценить массу M и гравитационный радиус R_g объекта, то из (2.2) определится g, т.е. мощность (интенсивность) центра притяжения.
   Гравитационное поле, создаваемое массой M, по закону (1.1) является универсальным - частицы, находящиеся на определенных расстояниях от центра притяжения, испытывают более сильное притяжение (1.2), а частицы, оказавшиеся на сравнительно больших расстояниях (в силу диссипации, взрыва и др.), будут испытывать более слабое - ньютоново гравитационное притяжение (1.3).

   Институт механики НАН РА
E-mail: aghal@mechins.sci.am

Литература

    1. Аппель П. Теоретическая механика. Т. 1. М. Гос. изд. физ-мат. лит. 1960. 515 с.
    2. Layzer D. Constructing the Universe. New York. Scientific American Books. Inc. 1984. 324 p.
    3. Киттель Ч., Найт У., Рудерман М. Механика. М. Наука. 1975. 480 с.

---