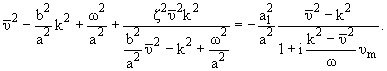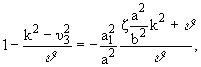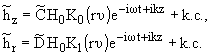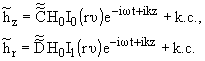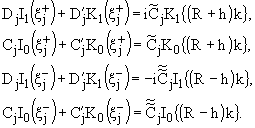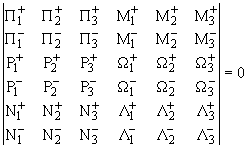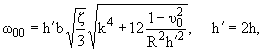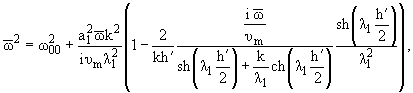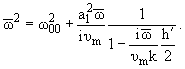МЕХАНИКА
УДК 539.1
Член-корреспондент НАН РА А. Г. Багдоев, А. В. Варданян,
С. В. Варданян
Определение линейных частот изгибных колебаний
магнитоупругой
цилиндрической оболочки
(Представлено 30/VIII 2005)
Ключевые слова: изгибные колебания, цилиндрическая оболочка, магнитоупругость
Рассматриваются линейные изгибные колебания
магнитоупругой цилиндрической оболочки в осевом магнитном поле. Решение получено
пространственным методом путем аналитических и численных
исследований.
B [1-5] при рассмотрении
изгибных колебаний магнитоупругих пластин и оболочек был применен осредненный
подход. С помощью нового пространственного подхода [6] магнитоупругие колебания
пластин рассмотрены в [7-9]. В настоящей работе использован пространственный
анализ для аналитического и численного определения частоты свободных изгибных
колебаний магнитоупругой цилиндрической оболочки.
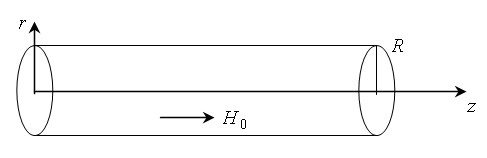
Пусть бесконечная цилиндрическая оболочка находится в осевом начальном
магнитном поле H0.
|
|
Уравнения
движения магнитоупругой среды в случае осевой симметрии,
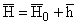 - магнитное поле, имеют вид [10,11]:
- магнитное поле, имеют вид [10,11]:
| a12 = |
H02
4pr
|
, z =
1 - |
b2
a2
|
, | |
|
¶2ur
¶r2
|
+ |
b2
a2
|
|
¶2ur
¶z2
|
+ z |
¶2uz
¶r¶z
|
+ |
1
r
|
|
¶ur
¶r
|
- |
1
r2
|
ur = |
1
a2
|
|
¶2ur
¶t2
|
- |
a12
a2
|
|
ж
з
и |
|
¶hr
¶z
|
- |
¶hz
¶r
|
|
ц
ч
ш |
, | |
(1) |
|
b2
a2
|
|
¶2uz
¶r2
|
+ |
¶2uz
¶z2
|
+ z |
¶2ur
¶r¶z
|
+ |
b2
a2
|
|
1
r
|
|
¶uz
¶r
|
+ |
z
r
|
|
¶ur
¶z
|
= |
1
a2
|
|
¶2uz
¶t2
|
, | |
где
для силы Лоренца учтено, что
|
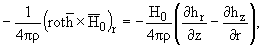
|
(2) |
|
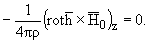
|
(3) |
Уравнение электромагнитной индукции
|
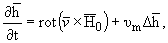
|
(4) |
где
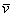 -
вектор скорости,
-
вектор скорости,
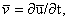
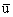 - перемещения, с учетом
соотношений
- перемещения, с учетом
соотношений
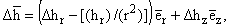 где
где 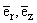 - единичные орты по осям r, z, Dj = [1/r][(¶)/(¶r)](r[(¶j)/(¶r)]) + [(¶2j)/(¶z2)], дает в
проекции на оси r, z
- единичные орты по осям r, z, Dj = [1/r][(¶)/(¶r)](r[(¶j)/(¶r)]) + [(¶2j)/(¶z2)], дает в
проекции на оси r, z
|
¶hr
¶t
|
= H0 |
¶2ur
¶t¶z
|
+ nm |
ж
з
и |
|
¶2hr
¶r2
|
+ |
1
r
|
|
¶hr
¶r
|
+ |
¶2hr
¶z2
|
- |
hr
r2
|
|
ц
ч
ш |
, | |
|
¶hz
¶t
|
= -H0 |
ж
з
и |
|
¶2ur
¶t¶r
|
+ |
1
r
|
|
¶ur
¶t
|
|
ц
ч
ш |
+ nm |
ж
з
и |
|
¶2hz
¶r2
|
+ |
1
r
|
|
¶hz
¶r
|
+ |
¶2hz
¶z2
|
|
ц
ч
ш |
. | |
Ищем решение (3),(5) в виде распространяющейся в направлении оси z
плоской волны
| ur = AjI1(x)e-iwt+ikz + AўjK1(x)e-iwt+ikz + к.c., | |
| uz = BjI0(x)e-iwt+ikz + BўjK0(x)e-iwt+ikz + к.c., | |
(6) |
| hz = CjH0I0(x)e-iwt+ikz + CўjH0K0(x)e-iwt+ikz + к.c., | |
| hr = DjH0I1(x)e-iwt+ikz + DўjH0K1(x)e-iwt+ikz + к.c., | |
где
I0,1(x), K0,1(x) - функции Бесселя мнимого аргумента, причем по j
суммируется от 1 до 3. Учитывая соотношения
| Iў0(x) = I1(x),
Kў0(x) = -K1(x), | |
|
dI1(x)
dx
|
+ |
1
x
|
I1(x) = I0(x),
|
dK1(x)
dx
|
+ |
1
x
|
K1(x) = -K0(x), | |
(7) |
можно из (3), (5), (6) получить:
| Aj |
ж
з
и |
nj2 - |
b2
a2
|
k2 + |
w2
a2
|
|
ц
ч
ш |
+ ziknjBj = |
a12
a2
|
(njCj - ikDj), | |
|
ж
з
и |
|
b2
a2
|
nj2 - k2 + |
w2
a2
|
|
ц
ч
ш |
Bj + ziknjAj = 0, | |
| Cj = |
iwnj
cj
|
Aj,
Dj = |
wkAj
cj
|
, cj = -iw + nmk2 - nmnj2, | |
(8) |
| Aўj |
ж
з
и |
nj2 - |
b2
a2
|
k2 + |
w2
a2
|
|
ц
ч
ш |
- ziknjBўj = |
a12
a2
|
(-njCўj - ikDўj), | |
| Bўj |
ж
з
и |
|
b2
a2
|
nj2 - k2 + |
w2
a2
|
|
ц
ч
ш |
- ziknjAўj = 0, Cўj = - |
iwnj
cj
|
Aўj, Dўj = |
wkAўj
cj
|
, | |
где
по j не суммируется. Таким образом, связи Aўj, -Cўj, Dўj с
-Bўj не отличаются
знаком от Aj, Cj, Dj с Bj и
окончательное уравнение для
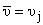 будет одним и тем
же:
будет одним и тем
же:
|
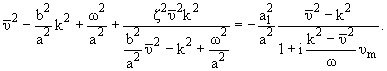
|
(9) |
Полученное уравнение такое же, как и для пластин [7], причем для малых
[(a12)/(a2)] и не больших nm
|
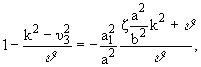
|
(10) |
| n12 = k2 - |
w2
a2
|
- |
a12
a2
|
|
ж
з
и |
k2 - |
w2
a2
|
|
ц
ч
ш |
|
ж
з
и |
1 + |
w2
a2J
|
|
ц
ч
ш |
, | |
(11) |
| n22 = k2 - |
w2
a2
|
+ |
a12
b2
|
k2 + |
w2a12k2
b4J
|
, J = i |
w
nm
|
. | |
(12) |
Таким образом, связи Aj, Cj, Dj через
Bj такие же, как для пластины, и такие же, как для Aўj, -Cўj, Dўj через
-Bўj. Для
завершения решения задачи следует записать граничные условия для r = R - h, r = R + h
|
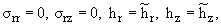
|
(13) |
где
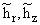 есть возмущенное магнитное поле вне оболочки. Первые два
условия (13) дают на указанных границах
есть возмущенное магнитное поле вне оболочки. Первые два
условия (13) дают на указанных границах
| a2 |
¶ur
¶r
|
+ |
ж
з
и |
a2 - 2b2 |
ц
ч
ш |
|
ж
з
и |
|
ur
r
|
+ |
¶uz
¶z
|
|
ц
ч
ш |
= 0, |
¶ur
¶z
|
+ |
¶uz
¶r
|
= 0. | |
Подставляя сюда (6) и полагая zў = z - [(b2)/(a2)], получим
| AjnjIў1(xj±) + zўAjnj |
1
xj±
|
I1(xj±) + AўjnjKў1(xj±) + | |
| + zўAўjnj |
1
xj±
|
K1(xj±) + zўBjikI0(xj±) + zўBўjikK0(xj±) = 0, | |
(14) |
| ikAjI1(xj±) + ikAўjK1(xj±) + BjI1(xj±)nj - BўjK1(xj±)nj = 0, | |
где
по j суммируется от 1 до 3, xj± = (R ± h)nj. Осталось выполнить условия
|
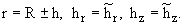
|
(15) |
При
r > R + h, n = k
|
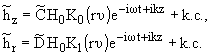
|
(16) |
При
r < R - h
|
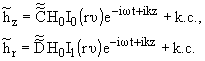 |
(17) |
Используя уравнение
и
подставляя в него (16), (17), получим
|
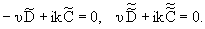 |
(18) |
Условия (15) дают с учетом (6)
Итак, имеют место четыре уравнения (14), к которым
добавятся два уравнения, получаемые из последних соотношений исключением
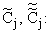
|
wkAj
cj
|
I1(xj+) + |
wkAўj
cj
|
K1(xj+) = i |
K1{(R + h)k}
K0{(R + h)k}
|
|
м
н
о |
|
iwnj
cj
|
AjI0(xj+) - |
iwnj
cj
|
AўjK0(xj+) |
ь
э
ю |
, | |
|
wkAj
cj
|
I1(xj-) + |
wkAўj
cj
|
K1(xj-) = -i |
I1{(R - h)k}
I0{(R - h)k}
|
|
м
н
о |
|
iwnj
cj
|
AjI0(xj-) - |
iwnj
cj
|
AўjK0(xj-) |
ь
э
ю |
. | |
Здесь по j суммируется от 1 до 3. К (14) и (19) следует добавить
| Aj = - |
1
ziknj
|
|
ж
з
и |
|
b2
a2
|
nj2 - k2 + |
w2
a2
|
|
ц
ч
ш |
Bj, | |
(20) |
| Aўj = |
1
ziknj
|
|
ж
з
и |
|
b2
a2
|
nj2 - k2 + |
w2
a2
|
|
ц
ч
ш |
Bўj, | |
где
по j не нужно суммировать. Система (14), (19) представляет однородные уравнения
относительно A1,2,3, Aў1,2,3 и
детерминантное уравнение имеет вид
|
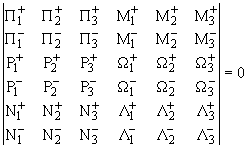 |
(21) |
где приняты следующие обозначения:
|
Х |
±
j
|
= njIў1(xj±) + znj |
I1(xj±)
xj±
|
+ z |
Bj
Aj
|
ik I0(xj±), | |
| Mj± = njKў1(xj±) + znj |
K1(xj±)
xj±
|
+ z |
Bўj
Aўj
|
ikK0(xj±), | |
| Pj± = ik I1(xj±) + |
Bj
Aj
|
njI1(xj±), Wj± = ikK1(xj±) - |
Bўj
Aўj
|
njK1(xj±), | |
| Nj+ = |
wk
cj
|
I1(xj+) + |
wnj
cj
|
|
K1{(R + h)k}
K0{(R + h)k}
|
I0(xj+),
| |
| Nj- = |
wk
cj
|
I1(xj-) - |
wnj
cj
|
|
I1{(R - h)k}
I0{(R - h)k}
|
I0(xj-), | |
| Lj+ = |
wk
cj
|
K1(xj+) - |
wnj
cj
|
|
K1{(R + h)k}
K0{(R + h)k}
|
K0(xj+),
| |
| Lj- = |
wk
cj
|
K1(xj-) + |
wnj
cj
|
|
I1{(R - h)k}
I0{(R - h)k}
|
K0(xj-). | |
При численном расчете уравнения (21) для определения корней w = w(k) дисперсионного уравнения
можно в нем все cj разделить на -iw, и поскольку для c3 имеет место (10), можно третий и шестой столбцы
в (21) умножить на a12, и кроме того, в членах
a12N3±,
a12L3± считать, что [(a12)/(c3)] = -a2[1/(z[(a2k2)/(b2J)] + 1)]. Эти преобразования необходимы, чтобы проводить
вычисления в (21) также для упругого случая a1 = 0, для которого w = w00. Были проведены
расчеты Re w(k) корней трансцендентного уравнения (21)
вместе с расчетом корней n1,2,3(w,k) уравнения (9), причем в качестве первого приближения
взято (10)-(12), и дисперсионное уравнение для упругого случая a1 = 0
[10]
|
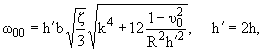 |
(22) |
Таблица 1
| a1/a k |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
| 5/105 |
95.25 |
142.071 |
262.124 |
420.1452 |
620.0876 |
| 1/104 |
94.9777 |
142.287 |
261.085 |
440.6969 |
640.2532 |
| 2/104 |
95.335 |
141.868 |
260.906 |
444.768 |
680.989 |
| 1/1000 |
95.3561 |
141.834 |
261.411 |
455.1 |
686.297 |
| 2/1000 |
94.0374 |
140.728 |
261.772 |
455.556 |
687.275 |
| 3/1000 |
37.4045 |
90.4933 |
118.291 |
445.074 |
687.825 |
| 4/1000 |
56.4103 |
118.236 |
176.434 |
224.562 |
687.133 |
| 5/1000 |
71.5075 |
141.546 |
243.717 |
287.003 |
354.739 |
| 6/1000 |
85.3117 |
168.453 |
259.745 |
347.349 |
425.96 |
| 7/1000 |
99.7618 |
146.206 |
291.762 |
399.149 |
498.628 |
| 8/1000 |
113.443 |
227.273 |
341.19 |
450.481 |
568.145 |
| 9/1000 |
127.268 |
252.926 |
378.975 |
509.944 |
639.966 |
| 1/100 |
141.459 |
276.627 |
425.007 |
563.777 |
686.181 |
| 2/100 |
282.78 |
565.711 |
848.694 |
1131.47 |
1414.49 |
| 3/100 |
424.182 |
848.397 |
1272.57 |
1696.54 |
2120.74 |
| 4/100 |
565.45 |
1130.9 |
1696.36 |
2261.87 |
2827.22 |
| 5/100 |
706.671 |
1413.34 |
2119.97 |
2826.6 |
3533.28 |
Таблица 2
| a1/a k |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
| 5/105 |
27.2162 |
108.861 |
244.912 |
435.349 |
680.126 |
| 1/104 |
27.2167 |
108.863 |
244.912 |
435.350 |
680.131 |
| 2/104 |
27.2181 |
108.865 |
244.92 |
435.358 |
680.139 |
| 1/1000 |
26.8179 |
108.876 |
245.064 |
435.587 |
680.444 |
| 2/1000 |
18.4247 |
107.53 |
244.906 |
435.966 |
681.169 |
| 2.2/1000 |
12.0007 |
106.756 |
244.691 |
435.981 |
681.323 |
| 2.4/1000 |
0.019999 |
105.698 |
244.374 |
435.952 |
681.456 |
| 2.6/1000 |
36.7695 |
104.288 |
243.927 |
435.861 |
681.567 |
| 2.8/1000 |
39.5979 |
102.436 |
243.320 |
435.700 |
681.640 |
| 3/1000 |
42.4263 |
100.05 |
242.527 |
435.449 |
681.675 |
| 3.3/1000 |
46.6689 |
95.1694 |
240.901 |
434.870 |
681.630 |
| 3.6/1000 |
50.9115 |
88.1594 |
238.636 |
433.981 |
681.418 |
| 3.8/100 |
53.7399 |
81.8141 |
236.693 |
433.184 |
681.170 |
| 4/1000 |
56.5683 |
113.137 |
234.337 |
432.191 |
680.819 |
| 5/1000 |
70.7102 |
141.42 |
213.726 |
423.299 |
676.911 |
| 5.1/1000 |
72.1244 |
144.249 |
216.373 |
421.946 |
676.272 |
| 5.3/1000 |
74.9528 |
149.906 |
224.858 |
418.912 |
674.804 |
| 5.5/1000 |
77.7812 |
155.562 |
233.343 |
415.402 |
673.093 |
| 5.8/1000 |
82.0237 |
164.047 |
246.071 |
409.127 |
669.985 |
| 6/1000 |
84.8521 |
169.704 |
254.556 |
339.408 |
424.260 |
| 7/1000 |
98.9937 |
197.987 |
296.981 |
395.975 |
494.969 |
| 7.1/1000 |
100.408 |
200.816 |
301.224 |
401.632 |
502.039 |
| 7.2/1000 |
101.822 |
203.644 |
305.466 |
407.288 |
509.11 |
| 7.5/1000 |
106.065 |
212.129 |
318.194 |
424.258 |
530.323 |
| 8/1000 |
113.135 |
226.271 |
339.406 |
452.541 |
565.676 |
| 9/1000 |
127.277 |
254.553 |
381.83 |
509.107 |
636.383 |
| 1/100 |
141.418 |
282.836 |
424.253 |
565.671 |
707.089 |
| 1.5/100 |
212.120 |
424.240 |
636.360 |
848.480 |
1060.60 |
| 2/100 |
282.814 |
565.629 |
848.443 |
1131.26 |
1414.07 |
| 3/100 |
424.169 |
848.337 |
1272.51 |
1696.67 |
2120.84 |
| 4/100 |
565.459 |
1130.92 |
1696.38 |
2261.835 |
2827.293 |
| 5/100 |
706.665 |
1413.33 |
2119.999 |
2826.657 |
3533.328 |
Таблица 3
| a1/a k |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
| 5/105 |
92.9628 |
140.546 |
260.579 |
444.445 |
686.196 |
| 1/104 |
92.9645 |
140.547 |
260.581 |
444.447 |
686.199 |
| 2/104 |
92.9713 |
140.553 |
260.587 |
444.455 |
686.209 |
| 1/1000 |
93.0612 |
140.633 |
260.748 |
444.694 |
686.519 |
| 2/1000 |
91.6883 |
139.811 |
260.682 |
445.111 |
687.28 |
| 2.2/1000 |
90.8207 |
139.28 |
260.507 |
445.138 |
687.436 |
| 2.4/1000 |
89.604 |
138.541 |
260.235 |
445.121 |
687.578 |
| 2.6/1000 |
87.9425 |
137.545 |
259.842 |
445.049 |
687.698 |
| 2.8/1000 |
85.715 |
136.235 |
259.304 |
444.906 |
687.787 |
| 3/1000 |
82.7625 |
134.544 |
258.591 |
444.678 |
687.835 |
| 3.3/1000 |
76.4733 |
131.118 |
257.124 |
444.137 |
687.807 |
| 3.6/1000 |
66.7971 |
126.31 |
255.066 |
443.3 |
687.626 |
| 3.8/100 |
57.1981 |
122.108 |
253.294 |
442.543 |
687.398 |
| 4/1000 |
42.7145 |
116.885 |
251.144 |
441.597 |
687.068 |
| 5/1000 |
0 |
57.2232 |
232.336 |
433.044 |
683.306 |
| 5.1/1000 |
0 |
41.7662 |
229.443 |
431.736 |
682.68 |
| 5.3/1000 |
0 |
0 |
222.897 |
428.805 |
681.257 |
| 5.5/1000 |
0 |
0 |
215.18 |
425.415 |
679.585 |
| 5.8/1000 |
0 |
0 |
200.87 |
419.343 |
676.551 |
| 6/1000 |
0 |
0 |
188.999 |
414.546 |
674.135 |
| 7/1000 |
0 |
0 |
49.9928 |
378.297 |
656.017 |
| 7.1/1000 |
0 |
0 |
0 |
373.193 |
653.526 |
| 7.2/1000 |
169.04 |
0 |
0 |
367.739 |
650.887 |
| 7.5/1000 |
343.729 |
0 |
0 |
348.982 |
642.003 |
| 8/1000 |
524.482 |
0 |
0 |
307.252 |
623.454 |
| 9/1000 |
786.114 |
0 |
0 |
125.186 |
566.883 |
| 1/100 |
1000.01 |
0 |
0 |
0 |
465.801 |
| 1.5/100 |
1872.11 |
2236.56 |
2115.96 |
1357.24 |
0 |
| 2/100 |
2646.98 |
3465.53 |
3875.19 |
4000.08 |
3857.77 |
| 3/100 |
4124.04 |
5658.21 |
6711.58 |
7490.67 |
8075.34 |
| 4/100 |
5568.49 |
7747.08 |
9330.34 |
10590. |
11632.9 |
| 5/100 |
7000.59 |
9798.89 |
11876.9 |
13570.8 |
15012.6 |
Таблица 4
| a1/a k |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
| 5/105 |
27.2167 |
108.867 |
244.949 |
435.466 |
680.415 |
| 1/104 |
27.2172 |
108.868 |
244.951 |
435.468 |
680.417 |
| 2/104 |
27.2185 |
108.871 |
244.957 |
435.476 |
680.427 |
| 1/1000 |
26.8186 |
108.888 |
245.102 |
435.708 |
680.735 |
| 2/1000 |
18.4253 |
107.541 |
244.95 |
436.1 |
681.485 |
| 2.2/1000 |
12.0003 |
106.768 |
244.74 |
436.117 |
681.637 |
| 2.4/1000 |
0 |
105.71 |
244.425 |
436.09 |
681.775 |
| 2.6/1000 |
0 |
104.298 |
243.979 |
436.004 |
681.89 |
| 2.8/1000 |
0 |
102.45 |
243.374 |
435.846 |
681.973 |
| 3/1000 |
0 |
100.064 |
242.581 |
435.599 |
682.014 |
| 3.3/1000 |
0 |
95.1842 |
240.96 |
435.024 |
681.975 |
| 3.6/1000 |
0 |
88.1736 |
238.7 |
434.144 |
681.78 |
| 3.8/100 |
0 |
81.8268 |
236.759 |
433.352 |
681.54 |
| 4/1000 |
0 |
73.5506 |
234.407 |
432.367 |
681.198 |
| 5/1000 |
0 |
0 |
213.803 |
423.509 |
677.346 |
| 5.1/1000 |
0 |
0 |
210.616 |
422.157 |
676.708 |
| 5.3/1000 |
0 |
0 |
203.38 |
419.13 |
675.258 |
| 5.5/1000 |
0 |
0 |
194.796 |
415.63 |
673.556 |
| 5.8/1000 |
0 |
0 |
178.695 |
409.363 |
670.472 |
| 6/1000 |
0 |
0 |
165.109 |
404.411 |
668.017 |
| 7/1000 |
0 |
0 |
0 |
366.929 |
649.631 |
| 7.1/1000 |
86.4275 |
0 |
0 |
361.637 |
647.104 |
| 7.2/1000 |
190.028 |
0 |
0 |
355.978 |
644.427 |
| 7.5/1000 |
352.736 |
0 |
0 |
336.472 |
635.416 |
| 8/1000 |
528.756 |
0 |
0 |
292.762 |
616.599 |
| 9/1000 |
787.29 |
0 |
0 |
81.7689 |
559.155 |
| 1/100 |
1000.0 |
0 |
0 |
0 |
456.082 |
| 1.5/100 |
1870.94 |
2236.36 |
2116.59 |
1359.63 |
0 |
| 2/100 |
2645.86 |
3464.96 |
3874.93 |
4000.07 |
3858.02 |
| 3/100 |
4123.19 |
5657.67 |
6711.19 |
7490.37 |
8075.12 |
| 4/100 |
5567.83 |
7746.64 |
9329.99 |
10589.7 |
11632.7 |
| 5/100 |
7000.05 |
9798.52 |
11876.6 |
13570.5 |
15012.4 |
здесь n0 - коэффициент
Пуассона, n0 = [1/3]. Результаты расчетов
действительной частоты Re w при значениях параметров
для алюминия [(b2)/(a2)] = [1/3], z
= [2/3], a = 105 см/с, r = 3 г/см3,
nm = 1000 см2/с., hў = 0.1 см, R = 103, 108 см,
k = 0.1, 0.2, 0.3, 0.4, 0.5 см-1 приведены в табл.
1,2. Проведено сравнение случая R = 108 см (табл.2) с результатами
решения соответствующего детерминантного уравнения для Re w(k) для пластин [12]. Результаты почти в точности совпадают,
что подтверждает правильность выводов и решений, приведенных в данной статье,
для оболочки. Мы сравнили также данные табл.1,2 с соответствующими результатами
осредненной теории, для которой дисперсионное уравнение получено в [10], которое
после некоторых преобразований может быть записано в виде [9]
|
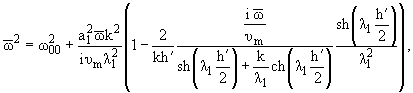 |
(23) |
где
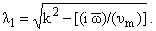 Для
вышеуказанных значений параметров |l1[(hў)/2]| << 1 и (23) дает
Для
вышеуказанных значений параметров |l1[(hў)/2]| << 1 и (23) дает
|
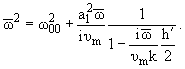 |
(24) |
Расчеты
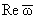 согласно (23) и (24) дают почти совпадающие величины, которые приведены в табл.
3,4. Сравнение результатов табл. 2, полученных по точному пространственному
подходу для R = 108 см, с результатами табл. 4, основанными на гипотезе
Кирхгофа, показываeт, что имеется качественное соответствие характера изменения
величин в кривых Re w(H0),
согласно (23) и (24) дают почти совпадающие величины, которые приведены в табл.
3,4. Сравнение результатов табл. 2, полученных по точному пространственному
подходу для R = 108 см, с результатами табл. 4, основанными на гипотезе
Кирхгофа, показываeт, что имеется качественное соответствие характера изменения
величин в кривых Re w(H0),
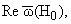 которые
начиная от значений w = w00,
которые
начиная от значений w = w00,
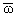 = w00 для случая
a1 = 0 уменьшаются, а затем возрастают, но количественно результаты
обеих таблиц совершенно различны. Те же заключения получены при сравнении табл.
1 с табл. 3 для R = 103 см.
= w00 для случая
a1 = 0 уменьшаются, а затем возрастают, но количественно результаты
обеих таблиц совершенно различны. Те же заключения получены при сравнении табл.
1 с табл. 3 для R = 103 см.
Институт
механики НАН РА
Литература
1. Амбарцумян С. А., Багдасарян Г. Е.,
Белубекян М. В. Магнитоупругость тонких оболочек и пластин. М.
Наука. 1977. 272 с.
2. Амбарцумян С. А.,
Багдасарян Г. Е. Электропроводящие пластинки и оболочки в
магнитном поле. М. Изд-во физ-мат. лит. 1996. 286 с.
3. Амбарцумян С. А., Белубекян М. В. Колебания и
устойчивость токонесущих пластин. Ереван. Изд-во НАН Армении. 1992. 124 с.
4. Багдоев А. Г., Мовсисян Л. А. - Изв. НАН Армении. Механика. 1999. Т. 52 N1. C.
25-30.
5. Саркисян В. С., Саркисян С. В.,
Джилавян С. А., Саргсян А. Л. - Механика. Ереван. ЕГУ. 1980. C.
45-56.
6. Новацки В. Теория
упругости. М. Мир. 1975. 863 с.
7. Багдоев
А. Г., Саакян С. Г. - Изв. РАН МТТ. 2001. N5. C. 35-42.
8. Bagdoev A. G., Vantsyan A. A. - Int. Journal of Solids and Structures. 2002. N39. P. 851-859.
9. Сафарян Ю. С. - Информационные технологии и управление. 2001. N2. C. 17-49.
10. Багдасарян Г. Е., Белубекян М. В. -
Изв. АН АрмССР. Механика. 1967. T. 20. N5. C. 21-27.
11. Кольский Г. Волны
напряжения в твердых телах. М. 1955. 192 с.
12. Багдоев А. Г., Варданян А. В. B cб.: Проблемы динамики
взаимодействия деформируемых сред. Горис. 2005. C. 77-81.
![]() -
вектор скорости,
-
вектор скорости,
![]()
![]() - перемещения, с учетом
соотношений
- перемещения, с учетом
соотношений
![]() где
где ![]() - единичные орты по осям r, z, Dj = [1/r][(¶)/(¶r)](r[(¶j)/(¶r)]) + [(¶2j)/(¶z2)], дает в
проекции на оси r, z
- единичные орты по осям r, z, Dj = [1/r][(¶)/(¶r)](r[(¶j)/(¶r)]) + [(¶2j)/(¶z2)], дает в
проекции на оси r, z ![]()
![]() согласно (23) и (24) дают почти совпадающие величины, которые приведены в табл.
3,4. Сравнение результатов табл. 2, полученных по точному пространственному
подходу для R = 108 см, с результатами табл. 4, основанными на гипотезе
Кирхгофа, показываeт, что имеется качественное соответствие характера изменения
величин в кривых Re w(H0),
согласно (23) и (24) дают почти совпадающие величины, которые приведены в табл.
3,4. Сравнение результатов табл. 2, полученных по точному пространственному
подходу для R = 108 см, с результатами табл. 4, основанными на гипотезе
Кирхгофа, показываeт, что имеется качественное соответствие характера изменения
величин в кривых Re w(H0),
![]() которые
начиная от значений w = w00,
которые
начиная от значений w = w00,
![]() = w00 для случая
a1 = 0 уменьшаются, а затем возрастают, но количественно результаты
обеих таблиц совершенно различны. Те же заключения получены при сравнении табл.
1 с табл. 3 для R = 103 см.
= w00 для случая
a1 = 0 уменьшаются, а затем возрастают, но количественно результаты
обеих таблиц совершенно различны. Те же заключения получены при сравнении табл.
1 с табл. 3 для R = 103 см.