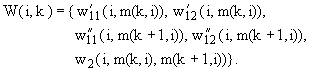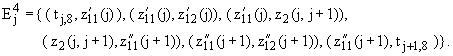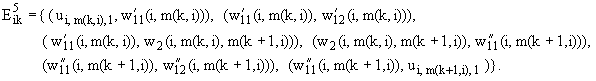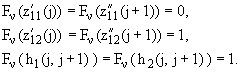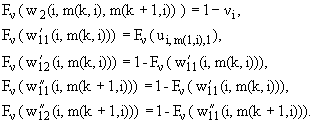Reports-2006-Vol106-N3-Balikyan

ПРИКЛАДНАЯ МАТЕМАТИКА

УДК 519.1

С. В. Баликян, Р. Р. Камалян

Об NP-полноте задачи существования локально-сбалансированного
2-разбиения двудольных графов G с D(G) = 4 при расширенном
определении окрестности вершины

(Представлено академиком Ю. Г. Шукуряном 3/IV 2006)

Ключевые слова: NP-полнота, локально-сбалансированный, разбиение, двудольный граф

   В работе рассматриваются неориентированные графы без кратных ребер и петель. Множество вершин графа G обозначается через V(G), множество ребер - через E(G). Наибольшая из степеней вершин графа G обозначается через D(G). Для вершины v О V(G) определим множество l(v) = {v} И {w О V(G)/(w,v) О E(G)}.
   2-разбиением графа G называется функция f : V(G) ® {0,1}.
   2-разбиение f графа G называется локально-сбалансированным, если для любой вершины v О V(G)

| |{w О l(v)/f(w) = 1}| - |{w О l(v)/f(w) = 0}| | Ј 1.

   Не определяемые понятия можно найти в [1-5].
   Пусть X = {x₁, ..., x_n} есть множество булевых переменных. Обозначим через 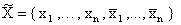множество литералов переменных множества X.
   Пусть D = {D₁, D₂,..., D_r} есть множество дизъюнкций, состоящих из литералов множества 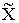. Через t(D_j) обозначим множество индексов тех переменных, литералы которых включены в дизъюнкцию D_j, j = 1, 2, .., r.
   Пусть K(x₁, ..., x_n) = D₁&D₂&...&D_r - конъюнктивная нормальная форма [6].
   Для i = 1, ..., n через M(i,K) обозначим множество {D_m(1,i), D_m(2,i), ..., D_m(s(i),i)} всех дизъюнкций из D, содержащих литерал переменной x_i (будем считать, что для i = 1, ..., n имеет место неравенство m(1,i) < m(2,i) < ... < m(s(i),i)).
   Для i = 1, ..., n через M₁(i,K) обозначим множество тех дизъюнкций из M(i,K), которые содержат литерал x_i, а через M₂(i,K) - множество тех дизъюнкций из M(i,K), которые содержат литерал 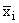. В [2] доказано, что NP-полной является
   Задача 1: ''3 - ВЫПОЛНИМОСТЬ''.
   Условие. Пусть X - множество булевых переменных, K(x₁, x₂, ..., x_n) = D₁&D₂&...&D_r - конъюнктивная нормальная форма, каждая дизъюнкция которой содержит в точности 3 литерала из .
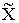   Вопрос. Существует ли последовательность (a₁, a₂, ..., a_n), где для i = 1, ..., n a_i О {0,1}, для которой K(a₁, a₂, ..., a_n) = 1 ?
   Задача 2:
   Условие. Дан граф G.
   Вопрос. Существует ли локально-сбалансированное 2-разбиение графа G?
   Теорема. Для двудольных графов G с D(G) = 4 задача 2 NP-полна.
   Доказательство. Принадлежность задачи 2 классу NP очевидна.
   Опишем полиномиальный алгоритм, сводящий задачу 1 к задаче 2 для двудольных графов G с D(G) = 4.
   Пусть в индивидуальной задаче I задачи 1 X = {x₁, ..., x_n} есть множество переменных и K(x₁, x₂, ..., x_n) = D₁&D₂&...&D_r - есть конъюнктивная нормальная форма.
   Определим граф G(I).
   Для i = 1, ..., n, j = 1, ..., r положим:

V_ij =

м
п
н
п
о

Ж,

если D_j П M(i,K),

{u_i,j,1},

если D_j П M₁(i,K),

{u_i,j,1, u_i,j,2, u_i,j,3, u_i,j,4},

если D_j П M₂(i,K).

Для j = 1, ..., r положим:

V_jⁱ=

n
И
i=1

V_ij

Для j = 1, ..., r положим:

V_j²= {t_j,1, t_j,2, t_j,3, t_j,4, t_j,5, t_j,6, t_j,7, t_j,8, t_j,9, t_j,10}.

Для j = 1, ..., r положим:

V_j= V_j¹

V_j².

Положим:

Z_r=

м
н
о

Ж,

если r > 1,

{z₁},

если r = 1.

Если r > 1, то для j = 1, ..., r - 1 положим:

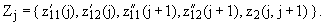
Для i = 1, ..., n при s(i) > 1 и k = 1, ..., s(i) - 1 положим:

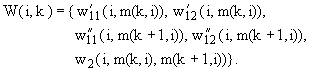Для i = 1, ..., n положим:

W_i =

м
п
н
п
о

Ж,

если s(i) = 1,

s(i)-1
И
k=1

W(i,k),

если s(i) > 1.

Положим: H_r= Ж.
Если r > 1, то для j = 1, ..., r - 1 положим:

H_j= {h₁(j,j + 1), h₂(j,j + 1)}.

Для j = 1, ..., r положим:

A_j= {a_j,1, a_j,2, a_j,3}.

Для i = 1, ..., n при s(i) > 1 и для k = 1, ..., s(i) положим:

B(i,k) =

м
н
о

{b_i,1(k), b_i,2(k), b_i,3(k)},

если k = 1, или k = s(i),

{b_i,1(k)},

если 1 < k < s(i).

Для i = 1, ..., n положим:

B_i =

м
п
н
п
о

{b_i,1(1)},

если s(i) = 1,

s(i)
И
k=1

B(i,k),

если s(i) > 1.

Положим:

V(G(I)) = (

r
И
j=1

(V_jИ Z_j И H_j И A_j)) И (

n
И
i=1

(W_iИ B_i)).

Для i = 1, ..., n, j = 1, ..., r положим:

E_ij¹ =

м
н
о

Ж,

если D_j П M₂(i,K),

{u_i,j,1, u_i,j,2}, {u_i,j,2, u_i,j,3}, {u_i,j,2, u_i,j,4},

если D_j О M₂(i,K).

Для j = 1, ..., r положим:

E_j¹=

n
И
i=1

E_ij¹.

Для i = 1, ..., n, j = 1, ..., r положим:

E_ij² =

м
п
п
п
н
п
п
п
о

Ж,

если D_j П M(i,K),

{u_i,j,1, t_j,1},

если D_j О M₁(i,K) и i №

max

t(D_j),

{u_i,j,3, t_j,1},

если D_j О M₂(i,K) и i №

max

t(D_j),

{u_i,j,1, t_j,5},

если D_j О M₁(i,K) и i =

max

t(D_j),

{u_i,j,3, t_j,5},

если D_j О M₂(i,K) и i =

max

t(D_j).

Для j = 1, ..., r положим:

E_j²=

n
И
i=1

E_ij².

Для j = 1, ..., r положим:

E_j³= {(t_j,1, t_j,2), (t_j,2, t_j,3), (t_j,3, t_j,4),

(t_j,4, t_j,5), (t_j,5, t_j,6), (t_j,6, t_j,7), (t_j,7, t_j,8), (t_j,3, t_j,9), (t_j,7, t_j,10)}

Положим:

E_r⁴ =

м
н
о

Ж,

если r > 1

t_1,8, z₁},

если r = 1.

Если r > 1, то для j = 1, ..., r - 1 положим:

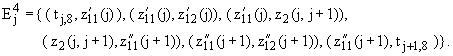
Для i = 1, ..., n при s(i) > 1 и для k = 1, ..., s(i) - 1 положим:

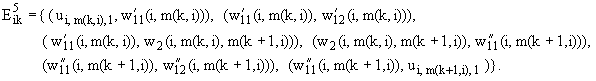
Для i = 1, ..., n положим:

E_i⁵ =

м
п
н
п
о

Ж,

если s(i) = 1,

s(i)-1
И
k=1

E_ik⁵,

если s(i) > 1.

Положим: E_r⁶= Ж.
Если r > 1, то для j = 1, ..., r - 1 положим:

E_j⁶= {(z₂(j,j + 1), h₁(j,j + 1)), (z₂(j,j + 1), h₂(j,j + 1))}.

Для j = 1, ..., r положим:

E_j⁷= {(t_j,4, a_j,1), (t_j,4, a_j,2), (a_j,1, a_j,3), (a_j,2, a_j,3)}.

Для i = 1, ..., n при s(i) > 1 и для k = 1, ..., s(i) положим:

E_ik⁸ =

м
п
н
п
о

{(u_i,m(k,i),1, b_i,1(k)), (u_i,m(k,i),1, b_i,2(k)),

(b_i,1(k), b_i,3(k)), (b_i,2(k), b_i,3(k))},

если k = 1 или k = s(i),

{(u_i,m(k,i),1, b_i,1(k))},

если 1 < k < s(i).

Для i = 1, ..., n положим:

E_i⁸ =

м
п
н
п
о

{(u_i,m(1,i),1, b_i,1(1))},

если s(i) = 1,

s(i)
И
k=1

E_ik⁸,

если s(i) > 1.

Положим:

E(G(I)) = (

r
И
j=1

(E_j¹ И E_j²И E_j³ И E_j⁴И E_j⁶ И E_j⁷)) И (

n
И
i=1

(E_i⁵И E_i⁸)).

   Граф G(I) определен.
   Ясно, что D(G(I)) = 4. С помощью лемм 1.1 и 1.2 работы [7] нетрудно показать, что G(I) является двудольным графом.
   Рассмотрим индивидуальную задачу I' задачи 2, в которой в качестве графа дан граф G(I). Покажем, что в индивидуальной задаче I ответ положительный тогда и только тогда, когда в индивидуальной задаче I' ответ положительный.
   Пусть для графа G(I) существует локально-сбалансированное 2-разбиение f. Очевидно, что f(t_1,8) = f(t_2,8) = ... = f(t_r,8). Без потери общности можно считать, что f(t_1,8) = 1. Легко видеть также, что для i = 1, ..., n

f(u_i,m(1,i),1) = f(u_i,m(2,i),1) = ... = f(u_{i,m(s(i),i),1}).

Для i = 1, ..., n и j = 1, ..., r определим множество V_ij³ Н V(G(I)) следующим образом:

V_ij³ =

м
п
н
п
о

Ж,

если D_j П M(i,K),

{u_i,j,1},

если D_j О M₁(i,K),

{u_i,j,3},

если D_j О M₂(i,K)

Для j = 1, ..., r положим:

V_j³=

n
И
i=1

V_ij³.

Легко видеть, что для j = 1, ..., r

V_j³= (l(t_j,1)\{t_j,1, t_j,2}) И (l(t_j,5)\{t_j,4, t_j,5, t_j,6}).

   Убедимся, что если для некоторого j₀, 1 Ј j₀ Ј r, f(t_j₀,8) = 1, то существуют 1₀ О {1,3} и i₀ О t(D_j₀) такие, что u_{i₀,j₀,1₀} О V_j₀³ и f(u_{i₀,j₀,1₀}) = 1.
   Действительно, из f(t_j₀,8) = 1 следует f(t_j₀,6) = 0, откуда: либо f(t_j₀,4) = 0 и существует 1₀ О {1,3} такое, что u_{maxt(D_j₀),j₀,1₀} О l(t_j₀,5)\{t_j₀,4, t_j₀,5, t_j₀,6} и f(u_{maxt(D_j₀),j₀,1₀}) = 1, либо f(t_j₀,4) = 1, откуда f(t_j₀,2) = 0 и cледовательно, существуют 1₀ О {1,3} и i₀ О t(D_j₀), i₀ № max t(D_j₀), для которых u_{i₀,j₀,1₀} О l(t_j₀,1)\{t_j₀,1, t_j₀,2} и f(u_{i₀,j₀,1₀}) = 1. Следовательно, существуют функции g₁: {1, ..., r} ® {1,3} и g₂: {1 , ..., r} ® {1, ..., n}, такие, что для j = 1, ..., r g₂(j) О t(D_j) и выполнены условия u_{g₂(j),j,g₁(j)} О V_j³ и f(u_{g₂(j),j,g₁(j)}) = 1.
   Определим набор m є (m₁, m₂, ..., m_n) следующим образом. Для i = 1, ..., n положим m_i= f(u_i,m(1,i),1). Покажем, что K(m₁, m₂, ..., m_n) = 1. Убедимся, что для любого j, 1 Ј j Ј r при x_i= m_i, i = 1, ..., n, дизъюнкция D_j конъюнктивной нормальной формы K(x₁, x₂, ..., x_n) принимает значение 1.
   Если D_j О M₁(g₂(j), K), то g₁(j) = 1 и m_g₂(j)= f(u_{g₂(j),m(1,g₂(j)),1}) = f(u_g₂(j),j,1) = 1, и утверждение очевидно. Если D_j О M₂(g₂(j), K), то g₁(j) = 3 и f(u_g₂(j),j,3) = 1, откуда f(u_g₂(j),j,1) = 0. Но f(u_g₂(j),j,1) = f(u_{g₂(j),m(1,g₂(j)),1}) = m_g₂(j), и утверждение доказано.
   Теперь предположим, что существует набор n є (n₁, n₂, ..., n_n), для которого K(n₁, n₂, ..., n_n) = 1.
   Опишем алгоритм построения функции F_v: V(G(I)) ® {0,1}, являющейся локально-сбалансированным 2-разбиением графа G(I).
   Алгоритм:
   Для i = 1, ..., n и j = m(1,i), m(2,i), ..., m(s(i), i) положим F_v(u_i,j,1) = v_i.
   Для i = 1, ..., n и j = 1, 2, ..., r при D_j О M₂(i,K) положим F_v(u_i,j,3) = 1 - F_v(u_i,j,1).
   Для j = 1, ..., r положим:

F_v(t_j,2) = 1 -

max

{F_v(v)/v О l(t_j,1)\{t_j,1, t_j,2}},

F_v(t_j,1) = 1 -

min

{F_v(v)/v О l(t_j,1)\{t_j,1, t_j,2}}.

Для j = 1, ..., r положим F_v(t_j,4) = 1 - F_v(t_j,2).
Так как K(n₁, n₂, ..., n_n) = 1, то для j = 1, ..., r

max{F_v(v)/v О l(t_j,5)\{t_j,5, t_j,6}} = 1.

Для j = 1, ..., r положим:

F_v(t_j,6) = 1 -

max

{F_v(v)/v О l(t_j,5)\{t_j,5, t_j,6}},

F_v(t_j,5) = 1 -

min

{F_v(v)/v О l(t_j,5)\{t_j,5, t_j,6}}.

Ясно, что F_v(t_1,6) = F_v(t_2,6) = ... = F_v(t_r,6) = 0.
Для j = 1, ..., r положим:

F_v(t_j,8) = 1,

F_v(t_j,7) = 1, F_v(t_j,10) = 0, F_v(t_j,3) = 1 - F_v(t_j,2), F_v(t_j,9) = 1 - F_v(t_j,3).

   Для j = 1, ..., r - 1 положим F_v(z₂(j,j + 1)) = 0.
   Если r = 1, положим F_v(z₁) = 0.
   Если r > 1, то для j = 1, ..., r - 1 положим:

Для j = 1, ..., r положим:

F_v(a_j,1) = F_v(a_j,2) = 1 - F_v(t_j,4),

F_v(a_j,3) = 1 - F_v(a_j,1).

Для i = 1, ..., n и j = 1, ..., r при D_j О M₂(i,k) положим:

F_v(u_i,j,2) = 1 - F_v(u_i,j,3),

F_v(u_i,j,4) = 1 - F_v(u_i,j,2).

Для i = 1, ..., n при s(i) > 1 и для k = 1, ..., s(i) - 1 положим:

Для i = 1 при s(i) = 1 положим:

F_v(b_i,1(1)) = 1 - F_v(u_i,m(1,i),1).

Для i = 1, ..., n при s(i) > 1 и для k = 2, ..., s(i) - 1 положим:

F_v(b_i,1(k)) = 1 - F_v(u_i,m(k,i),1).

Для i = 1, ..., n при s(i) > 1 положим:

F_v(b_i,1(1)) = F_v(b_i,2(1)) = 1 - F_v(u_i,m(1,i),1),

F_v(b_i,3(1)) = 1 - F_v(b_i,1(1)).

Для i = 1, ..., n при s(i) > 1 положим:

F_v(b_i,1(s(i))) = F_v(b_i,3(s(i))) = 1 - F_v(u_{i,m(s(i),i),1}),

F_v(b_i,2(s(i))) = 1 - F_v(b_i,1(s(i))).

Алгоритм завершен. Легко видеть, что функция F_v является локально-сбалансированным 2-разбиением графа G(I). Теорема доказана.
Настоящее исседование поддержано целевой программой 04-10-31 РА.

Ереванский государственный университет
Институт проблем информатики и автоматизации НАН РА

Литература

    1. Harary F. Graph Theory. Addison-Wesley. Reading. MA. 1969.
    2. Cook S. A. - Proc. 3^rd Ann. ACM Symp. On Theory of Computing. Association for Computing Machinery. New York. 1971. P. 151-158.
    3. Garey M. R., Jonson D. S. Computers and Intractability: A Guid to the Theory of NP-completeness. San Francisco: W. H. Freman & Company. Publishers. 1979.
    4. Papadimitriou C. H., Steiglitz K. - Combinatorial optimization: Algorithms and Complexity. PRENTICE-HALL. INC Englewood Cliffs. New Jersey. 1982.
    5. Karp R. M. - Complexity of Computer Computations. Eds. R. E. Miller and J. W. Thatcher. Plenum Press. New York. 1972. P. 85-103.
    6. Яблонский С. В. Введение в дискретную математику. М. Наука. 1986. 384 с.
    7. Мкртчян В. В. О сложности задач построения в графе максимальных паросочетаний специального типа. Kaнд. дис. ИПИА НАН РА. 2006. 150 с.