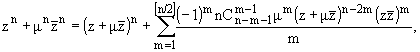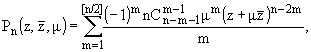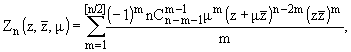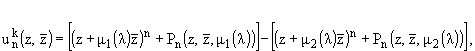МАТЕМАТИКА
УДК 517.98
Г. А. Саргсян
О собственных функциях смешанной задачи для одного
уравнения,
не разрешенного относительно старшей производной по времени
(Представлено академиком А. А. Талаляном 6/VI 2006)
Ключевые слова: смешанная задача, полнота, квадратичный пучок, собственная
функция
Спектральные свойства как линейных, так и
полиномиальных операторных пучков, порожденных смешанными задачами, не
разрешенными относительно старшей производной по времени, изучались различными
авторами [1]. Интерес к этой проблеме, не только практический, но и чисто
математический, связан с движением тяжелой идеальной несжимаемой жидкости и
малыми колебаниями вращающейся идеальной жидкости в задаче о колебаниях
электромагнитных и акустических волноводов. Все эти задачи при разделении и
определении переменной времени t сводятся к изучению квадратичного операторного
пучка. Для квадратичного пучка ставится вопрос о так называемой двукратной
полноте системы собственных и присоединенных элементов, впервые введенной и
изученной в работе М. В. Келдыша [2].
Рассмотрим следующую смешанную задачу:
|
¶2
¶t2
|
|
ж
з
и |
|
¶2u
¶x2
|
+ |
¶2u
¶y2
|
|
ц
ч
ш |
+ 2 |
¶
¶t
|
|
¶2u
¶x¶y
|
+ |
¶2u
¶y2
|
= 0, | |
(1) |
| u|t=0 = u0(x,y),
|
¶u
¶t
|
|
к
к
к |
t=0
|
= u1(x,y), | |
(2) |
где G -
гладкий контур, ограничивающий замкнутую односвязную область W в плоскости x,y. Известно, что если u0,
u1 О C2 и обращаются в нуль на
границе G, то решение задачи (1)-(3) существует для
всех t,x,y О W, аналитично по
t и дважды непрерывно дифференцируемо по x,y в W. Это
утверждение легко доказать путем определения ui из (1), (2), где
причем
Назовем число l собственным числом уравнения
| Ll(u) = l2 |
ж
з
и |
|
¶2u
¶x2
|
+ |
¶2u
¶y2
|
|
ц
ч
ш |
+ 2l |
¶2u
¶x¶y
|
+ |
¶2u
¶y2
|
= 0, | |
(5) |
если существует функция u О
1W2 |
(W) такая, что
для всех бесконечно дифференцируемых
и финитных в W функций j.
Собственные числа
уравнения (5) при наличии полной системы собственных функций характеризуют
поведение решений смешанной задачи при t ® Ґ. Смешанные задачи уравнения имеют вид
где A -
эллиптический оператор второго порядка, M - дифференциальный оператор того же
порядка. Исследование поведения t ® Ґ решений этих задач приводит к исследованию некоторого
ограниченного самосопряженного оператора в гильбертовом пространстве, спектр
которого совпадает с теми значениями l, при которых
оператор (lA + M)u является
гиперболическим.
Для этого оператора в
некоторых случаях удается построить систему обобщенных собственных функций [3],
инвариантные подпространства в которых легко дать простым представлением
оператора, и исследовать асимптотику соответствующих решений смешанной задачи
(5), (6). В этой работе изучается однородная краевая задача Дирихле на
собственные значения в случае, когда область W -
единичный круг с центром в начале координат
|
¶2u
¶y2
|
+ 2l |
¶2u
¶x¶y
|
+ l2 |
ж
з
и |
|
¶2u
¶x2
|
+ |
¶2u
¶y2
|
|
ц
ч
ш |
= 0, | |
(7) |
l - спектральный
параметр.
В [4] приводится явное
представление полной совокупности полиномиальных собственных функций задачи (7),
(8) в соболевском пространстве
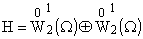 . .
В настоящей
работе предлагается метод построения в явном виде полной совокупности
полиномиальных собственных функций и собственных значений задачи (7), (8) через
известные полиномы Чебышева первого рода, а также специальное представление этих
функций.
Известно, что если оператор
самосопряжен, то его спектр лежит на вещественной прямой, т.е. если параметр
l комплексный, то l -
регулярная точка для резольвент. Подчеркнем, что спектр уравнения (7) совпадает
с комплексными значениями l, при которых это уравнение
эллиптично, т.е. характеристический многочлен имеет комплексные и различные
корни. Известно, что задача Дирихле в этом случае нефредгольмова. Уравнения
такого типа в случае, когда W - эллипс, исследованы Н.
Е. Товмасяном, который определил признаки существования нетривиальных решений
однородной задачи Дирихле и дал представление для таких решений
[5].
Общее решение уравнения (7) при любом
l имеет вид
| u(x,y) = j |
ж
з
и |
x - |
l - il2
l + l2
|
y |
ц
ч
ш |
+ y |
ж
з
и |
x - |
l - il2
l + l2
|
y |
ц
ч
ш |
. | |
(9) | Полагая z = x + iy, z = x - iy, имеем
|
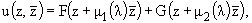
|
(10) | где
| m1(l) = |
1
1 + 2li
|
, m2(l) = 1 - 2li. | |
Значения параметра l, при которых задача (7),
(8) нетривиально разрешима, будем называть собственными значениями. Рассмотрим в
области W следующую задачу: найти те значения l, при которых существуют нетривиальные решения (7),
удовлетворяющие граничному условию (8).
Для
построения полной системы собственных функций уравнения (7) в пространстве
|
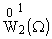 удобнее построить системы решений этого уравнения,
обращающихся в нуль на границе круга и являющихся полиномами по x,y. С этой
целью сформулируем несколько лемм без доказательств, установленные нами в работе
[4], которые используем при построении полной системы собственных функций задачи
Дирихле в пространстве удобнее построить системы решений этого уравнения,
обращающихся в нуль на границе круга и являющихся полиномами по x,y. С этой
целью сформулируем несколько лемм без доказательств, установленные нами в работе
[4], которые используем при построении полной системы собственных функций задачи
Дирихле в пространстве |
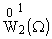 . .
Лемма 1. Для любого натурального n і 2 имеет место тождество
|
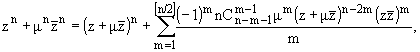
|
(11) | где [n/2] означает
целую часть числа n/2.
Обозначим через
|
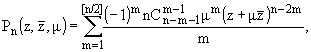
|
(12) |
|
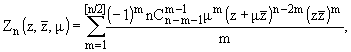
|
(13) | соответственно, порядка n - 2 и n, причем P1 = 0, P2 = 2m, K1 = 0.
Очевидно, что
|
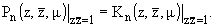
|
(14) | Лемма 2.
Полиномы
Pn(z,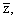 m) на
окружности круга W удовлетворяют рекуррентному
соотношению m) на
окружности круга W удовлетворяют рекуррентному
соотношению
|
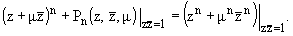
|
(15) | Лемма 3.
Полиномы
Pn(z,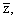 m) при
n = 2, 3, ... удовлетворяют рекуррентному соотношению m) при
n = 2, 3, ... удовлетворяют рекуррентному соотношению
|
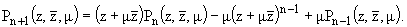
|
(16) | Перейдем к построению в явном виде полной совокупности нетривиальных
полиномиальных решений краевой задачи (7), (8).
Рассмотрим последовательность функции
|
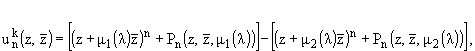
|
(17) | где
m1(l) = m2(l)e-[(2pki)/n], l =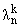 ,
n = 2, 3, ..., k = 1, 2, ..., (n - 1). ,
n = 2, 3, ..., k = 1, 2, ..., (n - 1). | |
Очевидно, что
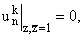 т.е. т.е.
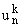 - собственные функции уравнения (7), соответствующие - собственные функции уравнения (7), соответствующие
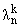 . . Замечание 1. Собственные значения краевой задачи (7), (8) являются
бесконечно кратными. Этот факт следует из того, что
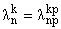 при любом P и что собственные
функции при любом P и что собственные
функции
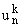 (x,y), соответствующие собственному значению (x,y), соответствующие собственному значению
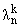 как полиномы различных
порядков, линейно незaвисимы. как полиномы различных
порядков, линейно незaвисимы.
Ниже мы
установим две теоремы, которые показывают, что построенные выше функции
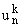 можно представить через известные полиномы Чебышева
первого рода, а также специальные представления этих
функций. можно представить через известные полиномы Чебышева
первого рода, а также специальные представления этих
функций.
После простых преобразований,
используя хорошо известную формулу cosnj, можно
сформулировать следующее представление функций
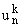 . .
Теорема 1. Систему собственных функций краевой
задачи (7), (8), соответствующих собственным значениям l =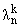 , можно
представить через полиномы Чебышева первого рода, т.е. , можно
представить через полиномы Чебышева первого рода, т.е.
|
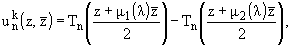
|
(18) | где
Tn(t) = cos(n arccos t),
m1(l) = m2(l)e-[(2pki)/n], l =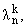 n = 2, 3, ..., k = 1, 2, 3, ..., (n - 1).
n = 2, 3, ..., k = 1, 2, 3, ..., (n - 1). | | Теорема 2.
Систему собственных
функций краевой задачи (7), (8) можно представить в специальном виде
|
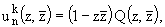 |
(19) | где
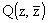 = = |
[n/2]
е
m=1
|
|
m
е
n = 1
|
|
n-2m
е
w = 0
|
|
m+w-1
е
s=0
|
|
(-1)m(n-m-1)m!m+w-1-sm2s
m!w!(n-2m-w)
|
, | |
| n = 2, 3, ..., k = 1, 2, ..., (n - 1). | | Доказательство. С учетом условия
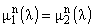 и однородности уравнения (7) имеем и однородности уравнения (7) имеем
Теорема доказана.
Теорема 3.
Система полиномиальных собственных
функций
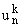 краевой задачи (7), (8) двукратно полна в краевой задачи (7), (8) двукратно полна в
|
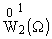 . .
Доказательство. Заметим, что двукратная полнота системы
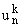 означает, что система означает, что система
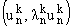 образует
полную систему в ортогональной сумме гильбертовых пространств образует
полную систему в ортогональной сумме гильбертовых пространств
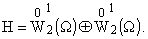 При каждом n уравнение m1(l) = m2(l)e-[(2pki)/n] имеет 2(n - 1) различных корней, которым соответствует 2(n - 1) различных собственных чисел для k = 1, 2 ,..., (n - 1). При каждом n уравнение m1(l) = m2(l)e-[(2pki)/n] имеет 2(n - 1) различных корней, которым соответствует 2(n - 1) различных собственных чисел для k = 1, 2 ,..., (n - 1).
Из специального
представления собственных функций следует, что существует n(n - 1) линейно независимых одночленов вида
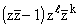 , где l + k Ј n - 2. Это значит, что линейной комбинацией с комплексными
коэффициентами векторов , где l + k Ј n - 2. Это значит, что линейной комбинацией с комплексными
коэффициентами векторов
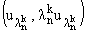 можно приблизить в метрике
комплексного пространства можно приблизить в метрике
комплексного пространства
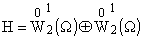 любую пару функций, принадлежащую этому
пространству. любую пару функций, принадлежащую этому
пространству.
Пусть Mn - линейная
замкнутая оболочка векторов
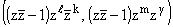 , где
l + k Ј n - 2, m + g Ј n - 2,
Hn - линейная оболочка векторов , где
l + k Ј n - 2, m + g Ј n - 2,
Hn - линейная оболочка векторов
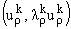 при r Ј n. Так как при r Ј n. Так как
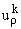 полиномы степени r, то для доказательства двукратной полноты достаточно
доказать, что размерности пространства Mn и Hn совпадают,
т.е. если векторы полиномы степени r, то для доказательства двукратной полноты достаточно
доказать, что размерности пространства Mn и Hn совпадают,
т.е. если векторы
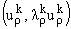 линейно независимы. Пусть это не так.
Тогда существует система чисел линейно независимы. Пусть это не так.
Тогда существует система чисел
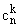 такая, что такая, что
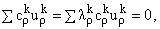 и решение смешанной задачи для
уравнения (1), построенное по нулевым начальным данным, u = и решение смешанной задачи для
уравнения (1), построенное по нулевым начальным данным, u =
В силу единственности решения указанной задачи u = 0. Отсюда следует, что
 =
0. Теорема
доказана. =
0. Теорема
доказана.
Заметим, что если при некотором
l существует решение уравнения (9), обращающееся в нуль
на G, то оно имеет вид (11) и для любой функции y
|
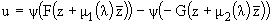 |
(*) |
удовлетворяет тому же уравнению и
нулевым граничным условиям. Таким образом, либо решение задачи Дирихле для
уравнения (9) единственно, либо существует бесконечно много линейно независимых
решений. Легко видеть, что полученные собственные значения расположены всюду
плотно на кривой |4l2 + 1| = 1 в комплексной
плоскости l и уравнение (7) при l = 0 параболично; для всех остальных значений l, расположенных на этой кривой, корни характеристического
многочлена комплексны и различны. Аналогично, легко получить собственные функции
уравнения
если L,N,M - линейные
дифференциальные операторы второго порядка с постоянными коэффициентами,
содержащие лишь вторые производные по x и y, а W -
эллипс, причем тип уравнения не играет роли.
Замечание 2. Отметим, что построениe в явном виде
полной системы полиномиальных решений задачи Дирихле уравнения (20) в круге
можно установить через функции Жуковского.
Военный авиационный институт им. маршала А. Ханферянца
Литература
1. Зеленяк Т. И. - ДАН СССР.
1964. Т. 158. №6. C. 1268-1270.
2. Келдыш М.
В. - ДАН СССР. 1951. Т. 77. №1. C. 11-14.
3. Александрян Р. А. - ТМО. 1960. Т. 9. C.
455-505.
4. Саргсян Г. А. - Уч. зап. ЕГУ. 1994. №1 (180). C. 19-25.
5. Товмасян Н. Е. - Изв. АН АрмССР. 1968. №6. C.
497-521.
|
![]() .
.