Ключевые слова: суммируемость по Абелю, гипорболическая метрика, Р-последовательность,
неравенство Бернулли
Числовой ряд
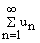 с комплексными числами называют
суммируемым методом Абеля (A-суммируемым) к сумме S,
с комплексными числами называют
суммируемым методом Абеля (A-суммируемым) к сумме S,
если степенной ряд
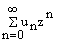 сходится в круге |z| < 1 и его сумма f(z) имеет
предел
сходится в круге |z| < 1 и его сумма f(z) имеет
предел
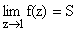 ,
,
когда z стремится к точке z = 1 вдоль действительной оси (по радиусу круга). Если сумма S конечна и
числовой ряд обладает дополнительными свойствами, то последнее условие в
указанном определении сохраняется и для случая, когда z стремится к z = 1 вдоль
любого непрерывного пути L, лежащего между двумя хордами единичной окружности
|z| = 1, проходящими через точку
|z| = 1, т.е. когда z ® 1 некасательным образом (см., например, [1], с. 135, 136). В
настоящей заметке предлагается дискретный вариант метода суммирования Абеля, в
котором предел функции f(z) рассматривается по некоторой, разумеется достаточно
"густой", последовательности точек круга |z| < 1, сходящейся к |z| = 1 произвольным образом, а степень "густоты"
последовательности характеризуется в терминах расстояния между ее
последовательными точками в гиперболической метрике на круге |z| < 1. Эта идея возникла в
связи с приложениями метода Абеля и, в частности, в связи с классической
теоремой Литтлвуда о сходимости числового ряда, суммируемого по Абелю. В
качестве следстия результатов этой статьи получаем заметное усиление утверждения
теоремы Литтлвуда.
1.
Определения, обозначения и формулировка основных
результатов.
Рассмотрим единичный круг
D : |z| < 1 z на комплексной
z-плоскости и гиперболическую метрику s на нем с
инфинитезимальным элементом ds(z) = (1 - |z|2)-1|dz|, z О
D. Последовательность {zk} точек z О D, k
О N, назовем s-последовательностью (слабой s-последовательностью), если
 и
и
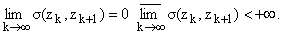
Ряд
с комплексными членами назовем
A(s) -суммируемым к конечной (бесконечной) сумме S,
если степенной ряд
сходится в круге D к голоморфной
функции f(z) и существует некоторая s-последовательность (слабая s-последовательность) (zk), по которой
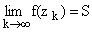 .
.
Из определений непосредственно следует, что каждый A-суммируемый ряд
будет также A(s)-суммируем к той же сумме. Обратные
утверждения справедливы при дополнительном ограничении на функцию f(z),
определяемую разложением (2), которое фoрмулируется в терминах ее сферической
производной
| f*(z) = |fў(z)| |
ж
и |
1 + |f(z)|2 |
ц
ш |
-1
|
, z О
D. | |
Теорема 1.
Если ряд (1) A(s)-суммируем к конечной (бесконечной) сумме S и функция f(z),
определяемая формулой (2), удовлетворяет условию
|
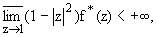
|
(3) |
то ряд (1) A-суммируем к
S.
На основании теоремы 1 получим
следующее усиление теоремы Литтлвуда.
Теорема 2. Если ряд (1) A(s)-суммируем к числу S и |un| = O([1/n]), n ® Ґ, то ряд сходится к сумме
S.
Усиление состоит в том, что в
условиях теоремы Литтлвуда вместо A(s)-суммируемости
ряда (1) предполaгается его A-суммируемость.
В пункте 3 приведены примеры, показывающие, что условие (3) существенно
для утверждения теоремы 1, а в случае S = Ґ оно не
улучшаемо в терминах роста сферической производной, a также пример,
показывающий, что в определении A(s)-суммируемости ряда
к конечной сумме условие существования предела функции f(z) по s-последовательности нельзя заменить условием существования
ее предела ни по какой слабой s-последовательности даже
при выполнении условия (3) в теореме 1.
Доказательство результатов базируeтся на свойствах P-последовательностей
мероморфных и голоморфных функций, изложенных в
[2,3].
2. Доказательства
результатов.
Доказательство теоремы 1. Рассмотрим сначала ряд (1), A(s)-суммируемый к конечной сумме S по некоторой s-последовательности (zk),
 , и допустим,
что он не суммируем по Абелю к сумме S, т.е. что число S не является радиальным
пределом
, и допустим,
что он не суммируем по Абелю к сумме S, т.е. что число S не является радиальным
пределом
в точке z = 1 голоморфной функции f(z), определяемой разложением (2).
Тогда, согласно теореме 9 ([2], с. 422.), в круге D функция f(z) обладает
некоторой P-последовательностью (xk), xk О D, сходящейся к z = 1
(т.е.
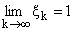 ). На основании теоремы 3 ([3], с. 397.) в
круге D найдется другая последовательность точек
). На основании теоремы 3 ([3], с. 397.) в
круге D найдется другая последовательность точек
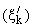 , которая обладает
свойствами:
, которая обладает
свойствами:
1)
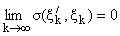 и
следовательно,
и
следовательно,
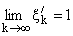 ,
,
2)
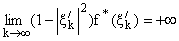 .
.
Свойства 1) и 2)
противоречат условию (3) теоремы 1.
Если ряд
(1) A(s)-суммируем к бесконечной сумме S по некоторой
слабой s-последовательности (zk),
 , то в вышеизложенных рассуждениях
существование у голоморфной функции f(z) некоторой P-последовательности (xk), xk О D,
, то в вышеизложенных рассуждениях
существование у голоморфной функции f(z) некоторой P-последовательности (xk), xk О D,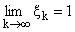 ,
обеспечивается ссылкой на ([3], теорема 9, с. 424).
,
обеспечивается ссылкой на ([3], теорема 9, с. 424).
Доказательство теоремы 2. По условию теоремы
существует константа C, 0 < C < +Ґ такая, что
|un| Ј [C/n] для всех n О N. Поэтому для
производной fў(z) функции, определяемой разложением
(2), справедлива оценка
| |fў(z)| Ј |
Ґ
е
n=1
|
n|un||z|n-1 Ј C |
Ґ
е
n=1
|
|z|n-1 = |
C
1 - |z|
|
, z О D, | |
из
которой следует удовлетворение функцией f(z) условию (3) теоремы 1. Согласно
утверждению теоремы 1 ряд (1) будет A-суммируем к числу S и обязан по теореме
Литтлвуда сходиться к S.
Замечание. Условие (3) в теореме 1 можно существенно ослабить в
случае, когда s-последовательность (zk), по
которой происходит A(s)-суммирование ряда (1), лежит на
радиусе круга D в точке z = 1. Обозначим символом D(j) угол раствора j, 0 < j < [(p)/2], образованный хордами
круга D в точке z = 1 и симметричный относительно радиуса круга D в точке z = 1.
Тогда при сделанном выше предположении на s-последовательность (zk) утверждение теоремы 1
останется справедливым, если условие (3) в нем заменить более слабым условием
|
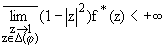
|
(3ў) |
для
некоторого j; 0 < j <
[(p)/2].
Действительно, в этом случае P-последовательность (xk) функции f(z) из доказательства теоремы 1,
согласно теореме 6 ([2], с. 421), также будет лежать на радиусе круга D в точке
z = 1. Гиперболическая геометрия круга D такова, что последовательность точек
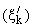 из
доказательства теоремы 1, удовлетворяющая условию
из
доказательства теоремы 1, удовлетворяющая условию
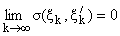 , обладает
следующим свойствoм: начиная с некоторого индекса все ее точки попадут
, обладает
следующим свойствoм: начиная с некоторого индекса все ее точки попадут
в D(j) для любого j, 0 < j < [(p)/2]. Последнее ведет к противоречию с
(3').
3.
Примеры.
Пример
1. Рассмотрим бесконечное произведение Бляшке B(z) =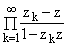 с нулями zk = 1 - [1/(k2)], k О N,
лежащими на действительной оси и имеющими
с нулями zk = 1 - [1/(k2)], k О N,
лежащими на действительной оси и имеющими
 .
Непосредственно проверяется, что
.
Непосредственно проверяется, что
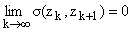 , т.е. что (zk)
образует s-последовательность. В статье [4] (пример 3)
отмечено, что голоморфная функция F(z) = B(z)expл(1 + z)(1 - z)-1ы, являясь отношением
ограниченных и голоморфных в круге D функций B(z) и expл(1 + z)(1 - z)-1ы, имеет F(zk) = 0
на s-последовательности (zk) и не имеет
предела, когда z стремится к z = 1 по действительной оси. Кроме того, для функции
F(z) ограниченного вида нарушено условие (3) теоремы 1, хотя каждый из ее
сомножителей, как хорошо известно (см. также ниже, пример 3), этому условию
удовлетворяет. Если рассмотреть тейлоровское разложение функции F(z) =
, т.е. что (zk)
образует s-последовательность. В статье [4] (пример 3)
отмечено, что голоморфная функция F(z) = B(z)expл(1 + z)(1 - z)-1ы, являясь отношением
ограниченных и голоморфных в круге D функций B(z) и expл(1 + z)(1 - z)-1ы, имеет F(zk) = 0
на s-последовательности (zk) и не имеет
предела, когда z стремится к z = 1 по действительной оси. Кроме того, для функции
F(z) ограниченного вида нарушено условие (3) теоремы 1, хотя каждый из ее
сомножителей, как хорошо известно (см. также ниже, пример 3), этому условию
удовлетворяет. Если рассмотреть тейлоровское разложение функции F(z) = , z О D, то заключаем, что ряд
, z О D, то заключаем, что ряд
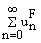 A(s)-суммируем, но он не суммируем по
A.
A(s)-суммируем, но он не суммируем по
A.
Пример 2. В статье
[5] (теорема 3) доказанo, что для любой функции m(r)
> 0, определенной и монотонно возрастающей на промежутке [0;1) и имеющей
 , можно указать такую бесконечную последовательность
(nj) натуральных чисел, что голоморфная в круге D функция g(z),
, можно указать такую бесконечную последовательность
(nj) натуральных чисел, что голоморфная в круге D функция g(z),
обладает
свойствами:
1)
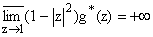 и
(1 - |z|2)g*(z) Ј
m(|z|) для всех z О D и |z| > r0, 0 <
r0 < 1;
и
(1 - |z|2)g*(z) Ј
m(|z|) для всех z О D и |z| > r0, 0 <
r0 < 1;
2) на действительной оси лежит бесконечная
последовательность (xk),
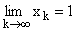 , нулей функции g(z) и
, нулей функции g(z) и
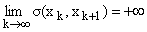 ;
;
3)
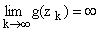 по s-последовательности (zk), лежащей на
действительной оси.
по s-последовательности (zk), лежащей на
действительной оси.
Рассмотрим тейлоровское
разложение функции g(z) =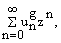 z О D. На основании вышеизложенного заключаем, что ряд
z О D. На основании вышеизложенного заключаем, что ряд
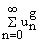 A(s)-
A(s)-
суммируем к S = Ґ и не суммируем по
A к S = Ґ. При этом свойство 1) показывает, что условие
(3) в теореме 1 (и условие (3') в замечании) не улучшаемо в терминах роста
сферической производной голоморфной функции в случае A(s)-суммируемости к бесконечной
сумме.
Случай A(s)-суммируемости к конечной сумме остается
открытым.
Пример 3.
Рассмотрим последовательность (zka),
zka = 1 - e-ak, k О N, где число a > 0
- фиксированное. Непосредственный подсчет показывает, что
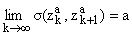 и,
следовательно, (zka) образуют слабую s-последовательность каким бы малым ни было число a > 0.
Так как сходится ряд
и,
следовательно, (zka) образуют слабую s-последовательность каким бы малым ни было число a > 0.
Так как сходится ряд
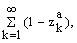 то сходится бесконечное
произведение Бляшке Ba(z),
то сходится бесконечное
произведение Бляшке Ba(z),
| Ba(z) = |
Ґ
Х
k=1
|
|
zka - z
1 - zka z
|
, z О D, | |
и
представляет в круге D ограниченную голоморфную функцию, имеющую нулями точки
zka, k О N. Поскольку для
произвольной голоморфной и ограниченной в круге D функции f(z) справедлива
оценка |fў(z)| = O([1/(1 - |z|)])|z| ® 1, (a
следовательно, и оценка (3)), функция Ba(z) удовлетворяет условию (3)
теоремы 1 для любого a > 0. Тейлоровское разложение Ba(z) = z О D, порождает ряд
z О D, порождает ряд
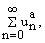 суммируемый к нулю по
слабой s-последовательности
(zka). Мы установим, что он не суммируем по A, если
докажем отсутствие у функции Ba(z) радиального предела в точке
z = 1.
суммируемый к нулю по
слабой s-последовательности
(zka). Мы установим, что он не суммируем по A, если
докажем отсутствие у функции Ba(z) радиального предела в точке
z = 1.
Рассмотрим последовательность
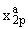 точек
точек
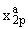 = 1 - 2-ae-2ap, p О N, и покажем, что
= 1 - 2-ae-2ap, p О N, и покажем, что
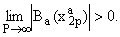 Так как
Так как
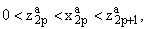 p О N, то для любого фиксированного p О N представим
p О N, то для любого фиксированного p О N представим
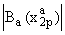 в виде
в виде
|

|
(4) |
Оценим каждый сомножитель в правой части (4) отдельно и для упрощения
изложения, не ограничивая общности, бyдем считать 0 < a < 1. После простых
преобрaзований с учетом значений
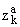 и
и
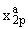 имеем
имеем
| T1(p) = |
2p
Х
k=1
|
|
1 - 2-ae-a(2p-k)
1 + 2-ae-a(2p-k) - 2-ae-2ap
|
, | |
(5) |
откуда
| T1(p) і
|
2p
Х
k=1
|
|
1 - 2-ae-a(2p-k)
1 + 2-ae-a(2p-k)
|
. | |
(6) |
Произведя в (6) замену индекса суммирования n =
2p - k, 0 Ј n Ј 2p - 1,
получим оценку
| T1(p) і
|
2p-1
Х
n = 0
|
|
1 - 2-ae-an
1 + 2-ae-an
|
. | |
(7) |
Для
оценки сверху T1(p) выделим в нем отдельным сомножителем правую часть
неравенства (6) и оценим сверху другой получающийся при этом сомножитель. На
основании (5) после простых преобрaзований имеем
| T1(p) = |
2p
Х
k=1
|
|
1 - 2-ae-a(2p-k)
1 + 2-ae-a(2p-k)
|
|
2p
Х
k=1
|
|
й
к
л |
1- |
2-ae-2ap
1 + 2-ae-a(2p-k)
|
|
щ
ъ
ы |
-1
|
. | |
(8) |
Cогласно неравенству Бернулли
|
2p
Х
k=1
|
|
й
к
л |
1 - |
2-ae-2ap
1 + 2-ae-a(2p-k)
|
|
щ
ъ
ы |
і 1 - |
2p
е
k=1
|
|
2-ae-2ap
1 + 2-ae-a(2p-k)
|
і 1 - 2pe-2ap. | |
(9) |
Для
всех достаточно больших p О N правая часть в (9)
положительна и следовательно, на основании (8), (9) и (7) для всех достаточно
больших p О N получим оценку
| T1(p) Ј
[1 - 2pe-2ap]-1 |
2p-1
Х
n = 0
|
|
1 - 2-ae-an
1 + 2-ae-an
|
, | |
(10) |
в которой использован тот же индекс
суммирования n = 2p - k, что и в
оценке (7).
Переходя к пределу при p ® Ґ на основании (7) и (10),
заключаем, что существует
|
lim
p®Ґ
|
T1(p) = |
Ґ
Х
n = 0
|
|
1 - 2-ae-an
1 + 2-ae-an
|
= A > 0. | |
(11) |
С множителем T2(p) в (4)
поступим аналогично. Простые преобрaзования с учетом значений
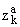 и
и
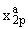 приводят к оценке
приводят к оценке
| T2(p) = |
Ґ
Х
k=2p+1
|
|
1-2ae-a(k-2p)
1+2ae-a(k-2p)-e-ak
|
і |
Ґ
Х
k=2p+1
|
|
1-2ae-a(k-2p)
1+2ae-a(k-2p)
|
= | |
| = |
Ґ
Х
m = 1
|
|
1-2ae-am
1+2ae-am
|
, | |
(12) |
в которой обозначено m = k - 2p, k і 2p + 1.
Поступая так же,
как и для T1(p), получим
| T2(p) = |
Ґ
Х
k=2p+1
|
|
1 - 2ae-a(k-2p)
1 + 2ae-a(k-2p)
|
|
Ґ
Х
k=2p+1
|
|
й
к
л |
1 - |
e-ak
1 + 2ae-a(k-2p)
|
|
щ
ъ
ы |
-1
|
. | |
(13) |
Согласно неравенству Бернулли для всех натуральных N > 2p + 1
справедлива оценка
|
N
Х
k=2p+1
|
|
й
к
л |
1 - |
e-ak
1 + 2ae-a(k-2p)
|
|
щ
ъ
ы |
-1
|
і 1 - |
N
е
k=2p+1
|
|
e-ak
1 + 2ae-a(k-2p)
|
і 1 - |
N
е
k=2p+1
|
e-ak =
| |
| = 1 - e-a(2p+1) |
1 - e-a(N-2p)
1 - e-a
|
, | |
на
основании которой после перехода к пределу при N ® Ґ получим оценку
|
Ґ
Х
k=2p+1
|
|
й
к
л |
1 - |
e-ak
1 + 2ae-a(k-2p)
|
|
щ
ъ
ы |
і 1 - |
e-a(2p+1)
1 - e-a
|
. | |
(14) |
Правая часть в (14) положительна для всех достаточно больших p О N, и, следовательно, на основании (13) и (14) для всех
достаточно больших p О N имеем оценку сверху
| T2(p) Ј
|
й
к
л |
1 - |
e-a(2p+1)
1 - e-a
|
|
щ
ъ
ы |
-1
|
|
Ґ
Х
m = 1
|
|
1 - 2ae-am
1 + 2ae-am
|
, | |
(15) |
в которой использован тот же индекс
суммирования m = k - 2p, что и в
оценке (12). Переходя к пределу при p ® Ґ, на основании (12) и (15) заключаем, что существует
|
lim
p®Ґ
|
T2(p) = |
Ґ
Х
m = 1
|
|
1 - 2ae-am
1 + 2ae-am
|
= B > 0. | |
(16) |
Окончательно на основании (4), (11) и (16) заключаем, что
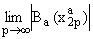 = AB > 0 и что функция Ba(z) не имеет
радиального предела в точке z = 1.
= AB > 0 и что функция Ba(z) не имеет
радиального предела в точке z = 1.
Автор
выражает искреннюю благодарность профессору В. И. Гаврилову за обсуждение
полученных результатов.
Государственный экономический университет
Армении
![]() с комплексными числами называют
суммируемым методом Абеля (A-суммируемым) к сумме S,
с комплексными числами называют
суммируемым методом Абеля (A-суммируемым) к сумме S, ![]() сходится в круге |z| < 1 и его сумма f(z) имеет
предел
сходится в круге |z| < 1 и его сумма f(z) имеет
предел
![]() ,
,
![]() и
и
![]()
![]() .
.![]() , и допустим,
что он не суммируем по Абелю к сумме S, т.е. что число S не является радиальным
пределом
, и допустим,
что он не суммируем по Абелю к сумме S, т.е. что число S не является радиальным
пределом ![]() ). На основании теоремы 3 ([3], с. 397.) в
круге D найдется другая последовательность точек
). На основании теоремы 3 ([3], с. 397.) в
круге D найдется другая последовательность точек
![]() , которая обладает
свойствами:
, которая обладает
свойствами:![]() и
следовательно,
и
следовательно,
![]() ,
,![]() .
.![]() , то в вышеизложенных рассуждениях
существование у голоморфной функции f(z) некоторой P-последовательности (xk), xk О D,
, то в вышеизложенных рассуждениях
существование у голоморфной функции f(z) некоторой P-последовательности (xk), xk О D,![]() ,
обеспечивается ссылкой на ([3], теорема 9, с. 424).
,
обеспечивается ссылкой на ([3], теорема 9, с. 424).![]() из
доказательства теоремы 1, удовлетворяющая условию
из
доказательства теоремы 1, удовлетворяющая условию
![]() , обладает
следующим свойствoм: начиная с некоторого индекса все ее точки попадут
, обладает
следующим свойствoм: начиная с некоторого индекса все ее точки попадут ![]() с нулями zk = 1 - [1/(k2)], k О N,
лежащими на действительной оси и имеющими
с нулями zk = 1 - [1/(k2)], k О N,
лежащими на действительной оси и имеющими
![]() .
Непосредственно проверяется, что
.
Непосредственно проверяется, что
![]() , т.е. что (zk)
образует s-последовательность. В статье [4] (пример 3)
отмечено, что голоморфная функция F(z) = B(z)expл(1 + z)(1 - z)-1ы, являясь отношением
ограниченных и голоморфных в круге D функций B(z) и expл(1 + z)(1 - z)-1ы, имеет F(zk) = 0
на s-последовательности (zk) и не имеет
предела, когда z стремится к z = 1 по действительной оси. Кроме того, для функции
F(z) ограниченного вида нарушено условие (3) теоремы 1, хотя каждый из ее
сомножителей, как хорошо известно (см. также ниже, пример 3), этому условию
удовлетворяет. Если рассмотреть тейлоровское разложение функции F(z) =
, т.е. что (zk)
образует s-последовательность. В статье [4] (пример 3)
отмечено, что голоморфная функция F(z) = B(z)expл(1 + z)(1 - z)-1ы, являясь отношением
ограниченных и голоморфных в круге D функций B(z) и expл(1 + z)(1 - z)-1ы, имеет F(zk) = 0
на s-последовательности (zk) и не имеет
предела, когда z стремится к z = 1 по действительной оси. Кроме того, для функции
F(z) ограниченного вида нарушено условие (3) теоремы 1, хотя каждый из ее
сомножителей, как хорошо известно (см. также ниже, пример 3), этому условию
удовлетворяет. Если рассмотреть тейлоровское разложение функции F(z) =![]() , z О D, то заключаем, что ряд
, z О D, то заключаем, что ряд
![]() A(s)-суммируем, но он не суммируем по
A.
A(s)-суммируем, но он не суммируем по
A.![]() , можно указать такую бесконечную последовательность
(nj) натуральных чисел, что голоморфная в круге D функция g(z),
, можно указать такую бесконечную последовательность
(nj) натуральных чисел, что голоморфная в круге D функция g(z), ![]() и
(1 - |z|2)g*(z) Ј
m(|z|) для всех z О D и |z| > r0, 0 <
r0 < 1;
и
(1 - |z|2)g*(z) Ј
m(|z|) для всех z О D и |z| > r0, 0 <
r0 < 1;![]() , нулей функции g(z) и
, нулей функции g(z) и
![]() ;
;![]() по s-последовательности (zk), лежащей на
действительной оси.
по s-последовательности (zk), лежащей на
действительной оси.![]() z О D. На основании вышеизложенного заключаем, что ряд
z О D. На основании вышеизложенного заключаем, что ряд
![]() A(s)-
A(s)-![]() и,
следовательно, (zka) образуют слабую s-последовательность каким бы малым ни было число a > 0.
Так как сходится ряд
и,
следовательно, (zka) образуют слабую s-последовательность каким бы малым ни было число a > 0.
Так как сходится ряд
![]() то сходится бесконечное
произведение Бляшке Ba(z),
то сходится бесконечное
произведение Бляшке Ba(z), ![]() z О D, порождает ряд
z О D, порождает ряд
![]() суммируемый к нулю по
слабой s-последовательности
(zka). Мы установим, что он не суммируем по A, если
докажем отсутствие у функции Ba(z) радиального предела в точке
z = 1.
суммируемый к нулю по
слабой s-последовательности
(zka). Мы установим, что он не суммируем по A, если
докажем отсутствие у функции Ba(z) радиального предела в точке
z = 1.![]() точек
точек
![]() = 1 - 2-ae-2ap, p О N, и покажем, что
= 1 - 2-ae-2ap, p О N, и покажем, что
![]() Так как
Так как
![]() p О N, то для любого фиксированного p О N представим
p О N, то для любого фиксированного p О N представим
![]() в виде
в виде ![]() и
и
![]() имеем
имеем 
