МЕХАНИКА
УДК 62.506.10
М. С. Габриелян, Л. А. Мазманян
Об оптимальном управлении колебательных движений круглой
пластинки
в конфликтных ситуациях
(Представлено академиком Г.Е. Багдасаряном 6/X 2005)
Ключевые слова: дифференциальная игра, оптимальные управляющие воздействия,
гипотетическое рассогласование, линейные колебания, бесселевы функции
1. Рассмотрим линейные
колебания круглой пластинки плотности r (r = g/g, где g - удельный вес материала, g - ускорение силы тяжести),
постоянной толщины h. Пластинка шарнирно оперта по контуру. Пусть на поверхности
пластинки на множестве положительной меры действуют две перпендикулярно
распределенные силы: F1(r,q,t) и
F2(r,q,t). Предполагая, что динамический
прогиб w(r,q,t) мал по сравнению с толщиной h, а
толщина, в свою очередь, мала по сравнению с радиусом r = a пластинки,
дифференциальное уравнение линейных колебаний будет ([1], с. 322, [2], с. 278)
|
D
h
|
С4w + |
g
g
|
|
¶2w
¶t2
|
= |
F1(r,q,t)
h
|
+ |
F2(r,q,t)
h
|
, | |
(1.1) |
где D = Eh3/12(1 - m2) - жесткость
пластинки, m - коэффициент Пуассона, E - модуль
упругости материала при растяжении (сжатии), а
| С2 = |
¶2
¶r2
|
+ |
1
r
|
|
¶
¶r
|
+ |
1
r2
|
|
¶2
¶q2
|
. | |
Края пластинки удовлетворяют следующим
условиям шарнирного опирания ([1], [2], с. 325):
| w(r,q,t) = 0,
Mr = 0 при r = a, | |
(1.2) |
где Mr = -D[[(¶2w)/(¶r2)] + m([1/r][(¶w)/(¶r)] + [1/(r2)][(¶2w)/(¶q2)]) ] изгибающий момент.
Пусть начальные условия будут
| w(r,q,t)|t=0 = j(r,q), |
¶w(r,q,t)
¶t
|
|t=0 = y(r,q), | |
(1.3) |
где j(r, q) и y(r, q) - соответственно начальный
прогиб и начальная скорость срединной поверхности.
Задача о собственных колебаниях круглой
пластинки (F1(r,q,t) = 0 и
F2(r,q,t) = 0) при условиях (1.2), (1.3)
решается методом разделения переменных ([1], с. 322, [3], с. 430)
| w(r,q,t) = W(r,q)T(t) = R(r)F(q)T(t), | |
(1.4) |
где T(t), F(q) и R(r) удовлетворяют уравнениям
| r2 |
d2R(r)
dr2
|
+ r |
dR(r)
dr
|
+ (±a2r2 - n2)R(r) = 0. | |
(1.7) |
Здесь n -
постоянная, а w собственная частота,
Функции F(q) и R(r) также удовлетворяют
следующим условиям ([3], с. 431):
| |R(0)| < Ґ (условия ограниченности),
| |
(1.9) |
| R(a) = 0 (граничное
условие), | |
(1.10) |
| Mr|r=a = 0 (граничное
условие), | |
(1.11) |
| F(q) = F(q + 2p) (условиe
периодичности). | |
(1.12) |
Нетривиальные периодические
решения для F(q) существуют
лишь при n2 = n2 (n - целое число)
и имеют вид ([3], с. 431)
| Fn(q) = Cncosnq + Dnsinnq, | |
(1.13) |
Cn, Dn
определяются из граничных и начальных условий.
Для определения функции R(r)
имеем уравнение (1.7) с однородными граничными условиями (1.9), (1.10) и (1.11).
Вводя новую переменную r = ar
в случае положительного знака в (1.7) и переменную r =
iar в случае отрицательного знака в (1.7), получим
дифференциальное уравнение Бесселя с индексом n ([4], с. 49)
|
d2R(r)
dr2
|
+ |
1
r
|
|
dR(r)
dr
|
+ |
ж
з
и |
1 - |
n2
r2
|
ц
ч
ш |
R(r) = 0. | |
(1.14) |
После подстановки r = r решение (1.14) будет
| R(r) = AnJn(ar) + BnJn(iar) + EnYn(ar) + FnYn(iar), | |
(1.15) |
где Jn(ar) - бесселева функция первого рода с индексом,
Yn(ar) - бесселева функция второго рода с
индексом, Jn(iar), Yn(iar) - модифицированные бесселевы функции.
Бесселевы
функции второго рода стремятся к бесконечности при r ®
0. Тогда коэффициенты En = 0, Fn = 0.
Собственные функции
данной краевой задачи имеют следующий вид:
|
| Wmn(r,J) = |
й
к
л
|
AmnJn |
ж
з
и
|
lmn |
r
a
|
ц
ч
ш
|
+ BmnJmn |
ж
з
и
|
ilmn |
r
a
|
ц
ч
ш
|
щ
ъ
ы
|
[Cmncosnq + Dmnsinnq], | |
| (m = 1, 2, ј; n = 0, 1, 2, ј). | | |
| |
(1.17) |
Собственные числа lmn = amna
определяются из уравнения
| 2lmna[In(lmn)Jn(lmn)] - (1 - m)[In(lmn)Jn+1(lmn) + Jn(lmn)In+1(lmn)] = 0. | |
(1.18) |
Решение уравнения (1.1) будем
искать в виде ряда
| w(r,q,t) = |
Ґ
е
m=1
|
|
Ґ
е
n=0
|
Wmn(r,q)Tmn(t), | |
(1.19) |
где Tmn(t) = w(r,q,t)Wmn(r,q)rdrdq.
w(r,q,t)Wmn(r,q)rdrdq.
Так как в области [0,a] × [0,2p]
функции (1.17) ортогональны с весом r, то функции F1(r,q,t), F2(r,q,t), j(r,q) и y(r,q) допускают следующие
разложения:
| F1(r,q,t) = |
Ґ
е
m=1
|
|
Ґ
е
n=0
|
umn(t)Wmn(r,q), F2(r,q,t) = |
Ґ
е
m=1
|
|
Ґ
е
n=0
|
vmn(t)Wmn(r,q), | |
| j(r,q) = |
Ґ
е
m=1
|
|
Ґ
е
n=0
|
jmn(t)Wmn(r,q), y(r,q) = |
Ґ
е
m=1
|
|
Ґ
е
n=0
|
ymn(t)Wmn(r,q), | |
(1.20) |
где
| umn(t) = |
a
у
х
0
|
2p
у
х
0
|
F1(r,q,t)Wmn(r,q)rdrdq, vmn(t) = |
a
у
х
0
|
2p
у
х
0
|
F2(r,q,t)Wmn(r,q)rdrdq, | |
| jmn = |
a
у
х
0
|
2p
у
х
0
|
j(r,q)Wmn(r,q)rdrdq, ymn = |
a
у
х
0
|
2p
у
х
0
|
y(r,q)Wmn(r,q)rdrdq. | |
Подставляя
(1.19) и (1.20) в уравнение (1.1), умножая последнее на rWmn(r,q) и интегрируя по r от нуля до a, а по q от нуля до 2p, получим для
определения функций Tmn(t) следующую систему дифференциальных
уравнений второго порядка:
|
d2Tmn(t)
dt2
|
=
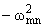 Tmn(t) + umn(t) + vmn(t),
(m = 1, 2, ј; n = 0, 1, 2, ј) Tmn(t) + umn(t) + vmn(t),
(m = 1, 2, ј; n = 0, 1, 2, ј) | |
(1.21) |
с начальными условиями
| Tmn(0) = |
a
у
х
0
|
2p
у
х
0
|
j(r,q)Wmn(r,q)rdrdq = jmn, | |
|
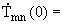 |
a
у
х
0
|
2p
у
х
0
|
y(r,q)Wmn(r,q)rdrdq = ymn. | |
(1.22) |
Квадрат частоты собственных
колебаний круглой пластинки имеет вид
|

|
(1.23) |
Предполагаем, что силы
F1(r,q,t) и F2(r,q,t) принадлежат классу L2 и удовлетворяют
условиям
|
й
л |
a
у
х
0
|
2p
у
х
0
|
[F1(r,q,t)]2drdq |
щ
ы |
1/2
|
= |
й
л |
k |
Ґ
е
m=1
|
|
Ґ
е
n=0
|
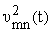 |
щ
ы |
1/2
|
Ј
P, | |
|
й
л |
a
у
х
0
|
2p
у
х
0
|
[F2(r,q,t)]2drdq |
щ
ы |
1/2
|
= |
й
л |
k |
Ґ
е
m=1
|
|
Ґ
е
n=0
|
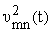 |
щ
ы |
1/2
|
Ј
Q | |
(1.24) |
равномерно по t О [0,T]. Здесь P,Q,T - заданные положительные числа, k -
постоянная.
Рассмотрим следующую игровую задачу. Пусть
первый игрок, распоряжающийся управлениями umn (m = 1, 2, ј; n = 0, 1, 2, ј), стремится
минимизировать значение величины

при самом упорном сопротивлении второго игрока,
распоряжающегося управляющими воздействиями vmn (m = 1, 2, ј; n = 0, 1, 2, ј), а второй
игрок, в свою очередь, стремится максимизировать значение величины

при самом упорном сопротивлении со стороны первого игрока. Величину
J (0 < J
Ј T) определим ниже. Динамика игры определяется
бесконечной линейной системой дифференциальных уравнений (1.21).
Такая задача была рассмотрена в работе [5],
где исследовано оптимальное управление механической системы мощности континуума,
когда на континуум действуют противоборствующие силы. Задача приводилась к
решению интегро-дифференциального уравнения с симметричным ядром и правой
частью. На основании этой работы исследованы задачи, системы которых описываются
частными прoизводными высшей степени [6,7]. Настоящая работа основана на этих
идеях.
2. С помощью метода
экстремального прицеливания составим гипотетическое рассогласование. Так как
собственные числа lmn (m = 1, 2, ј; n = 0, 1, 2, ј)
положительны, то вводя следующие обозначения:
|
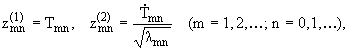
|
(2.1) |
систему дифференциальных уравнений
(1.21) можем записать в виде
|

|
(2.2) |
Определение. Задачу для системы (2.2) назовем регулярной, если она регулярна для
любых конечных m,n из (2.2).
Гипотетическое рассогласование для
сформулированной игровой задачи будет [5]
|
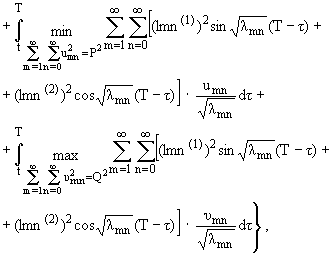 |
(2.3) |
где
Используя метод неопределенных коэффициентов
Лагранжа, для
 и
и
 получим [5,6]
получим [5,6]
|
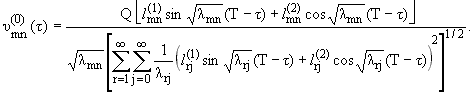 |
(2.4) |
Подставляя значения
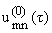 и
и
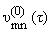 из (2.4) в (2.3),
получим
из (2.4) в (2.3),
получим
|
 |
(2.5) |
При условии P > Q выражение в фигурных
скобках в формуле (2.5) является вогнутой функцией по переменным
 и
и
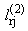 (r = 1, 2, ј ; j = 0, 1, 2, ј ),
следовательно, максимум в (2.5) при любых
(r = 1, 2, ј ; j = 0, 1, 2, ј ),
следовательно, максимум в (2.5) при любых
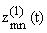 ,
,
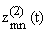 достигается на единственном векторе
достигается на единственном векторе
 (m = 1, 2, ј ; n = 0, 1, 2, ј ), т.е. при
любых начальных значениях игровая ситуация регулярна [7,8]. Получены уравнения,
из которых определяются компоненты вектора l0 [5,6].
(m = 1, 2, ј ; n = 0, 1, 2, ј ), т.е. при
любых начальных значениях игровая ситуация регулярна [7,8]. Получены уравнения,
из которых определяются компоненты вектора l0 [5,6].
Заметим, что
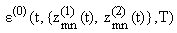 - ограниченная величина, так как ряды, участвующие в выражениях (2.5), сходятся,
следовательно, оптимальные управляющие воздействия, определяемые формулой (2.4)
равномерно по t О [0,T],
составляют сходящиеся квадратом ряды [5,9]. Для определения момента J в каждой ситуации нужно найти наименьший корень уравнения
- ограниченная величина, так как ряды, участвующие в выражениях (2.5), сходятся,
следовательно, оптимальные управляющие воздействия, определяемые формулой (2.4)
равномерно по t О [0,T],
составляют сходящиеся квадратом ряды [5,9]. Для определения момента J в каждой ситуации нужно найти наименьший корень уравнения
|
 |
(2.6) |
3. Так как
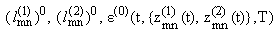 ,
,
 и
и
 (m = 1, 2, ј ; n = 0, 1, 2, ј ) трудно
представить в аналитической форме, то задачу решим численно.
(m = 1, 2, ј ; n = 0, 1, 2, ј ) трудно
представить в аналитической форме, то задачу решим численно.
Для численного примера возьмем круглую
пластинку из стали, которая имеет следующие значения параметров: a = 0,2м,
h = 0,001м, r = 7,9 · 103кг/м3,
E = 2 · 1011н/м2, m = 0,3, P = 8, Q = 2,
t = 0. Ограничимся случаями m = 2, двумя узловыми окружностями, а узловые диаметры
рассмотрим до n = 3.
Вычислены собственные числа lmn из уравнения (1.18), следовательно и квадрат
частоты собственных колебаний круглой пластинки из (1.23) для m = 2, n = 0,1,2,3:
Пусть начальный прогиб и начальная
скорость срединной поверхности будут
|
| j(r,q) = |
1
2 · 10120
|
r2qsinq, | |
| y(r,q) = |
1
1 · 10120
|
rqsinq. | | |
| |
(3.2) |
Рис. 1
Рис. 2
Учитывая эти значения, с помощью
программы «Mathematica 5.0» и «Microsoft Excel» численным методом вычислены
 (m = 2, n = 0,1,2,3), а
следовательно вычислены гипотетическое рассогласование из (2.5), и оптимальные
управляющие воздействия из (2.4).
(m = 2, n = 0,1,2,3), а
следовательно вычислены гипотетическое рассогласование из (2.5), и оптимальные
управляющие воздействия из (2.4).
На рис. 1-3 представлены
зависимости e0{T,0,6000},
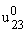 {t,0,30},
{t,0,30},
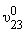 {t,0,30} соответственно.
{t,0,30} соответственно.
Рис. 3
Рис. 4
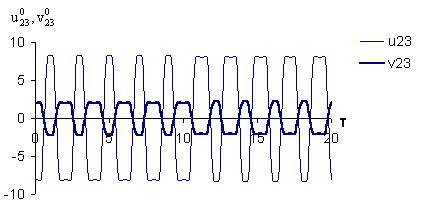
Из рис. 4 видно, что
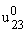 и
и
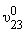 имеют противоположные
знаки на том же интервале времени. Остальные оптимальные управляющие
воздействия,
имеют противоположные
знаки на том же интервале времени. Остальные оптимальные управляющие
воздействия,
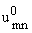 {t,0,30},
{t,0,30},
 {t,0,30}
(m = 2, n = 0,1,2) имеют тот же характер, что и
{t,0,30}
(m = 2, n = 0,1,2) имеют тот же характер, что и
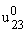 {t,0,30} (рис.2) и
{t,0,30} (рис.2) и
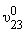 {t,0,30} (рис. 3).
{t,0,30} (рис. 3).
Из рис. 1-4 следует, что когда ресурсы
первого игрока больше, чем второго (P > Q), то задача всегда решается в
пользу первого, т.е. первый игрок, распоряжающийся управлением
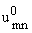 (m = 2, n = 0,1,2,3), гасит колебательное
движение оболочки при самом упорном сопротивлении со стороны второго игрока
(m = 2, n = 0,1,2,3), гасит колебательное
движение оболочки при самом упорном сопротивлении со стороны второго игрока
 (m = 2, n = 0,1,2,3). А второй игрок,
наоборот, при (P < Q) может увеличить амплитуду колебаний.
(m = 2, n = 0,1,2,3). А второй игрок,
наоборот, при (P < Q) может увеличить амплитуду колебаний.
Ереванский государственный университет
Литература
1. Филиппов А.П. Колебания упругих систем. М. Наука.
1956.
2. Лехницкий С.Г.
Анизотропные пластинки. М. Гостехиздат.
1957.
3. Тихонов А.Н., Самарский
А.А. Уравнения математической физики. М. Наука.
1972.
4. Ватсон Г.Н. Теория бесселевых функций. Ч. 1. М. ИЛ.
1949.
5. Габриелян М.С.
- Изв. НАН РА. Механика. 1998. N 4. С.
72-76.
6. Мазманян Л.А.
В сб.: Оптимальное управление, устойчивость и прочность
механических систем. Ереван. 2002. С. 48-52.
7.
Габриелян М.С., Мазманян Л.А. - Изв. НАН РА.
Механика. 2005. Т. 58. N 3.
8. Красовский Н.Н., Субботин А.И. Позиционные
дифференциальные игры. М. Наука. 1974.
9. Колмогоров А.Н., Фомин С.В. Элементы теории и
функционального анализа. М. Наука. 1989.
![]() w(r,q,t)Wmn(r,q)rdrdq.
w(r,q,t)Wmn(r,q)rdrdq.

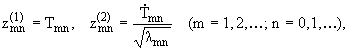

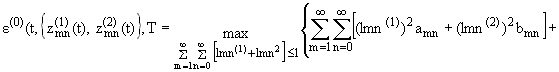
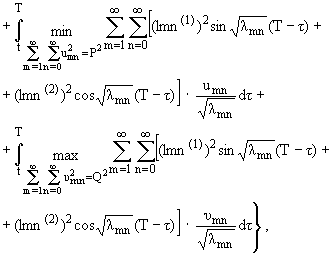
![]()
![]()
![]() и
и
![]() получим [5,6]
получим [5,6] 
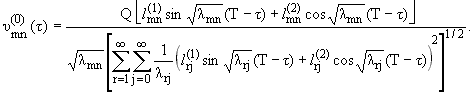
![]() и
и
![]() из (2.4) в (2.3),
получим
из (2.4) в (2.3),
получим 
![]() и
и
![]() (r = 1, 2, ј ; j = 0, 1, 2, ј ),
следовательно, максимум в (2.5) при любых
(r = 1, 2, ј ; j = 0, 1, 2, ј ),
следовательно, максимум в (2.5) при любых
![]() ,
,
![]() достигается на единственном векторе
достигается на единственном векторе
![]() (m = 1, 2, ј ; n = 0, 1, 2, ј ), т.е. при
любых начальных значениях игровая ситуация регулярна [7,8]. Получены уравнения,
из которых определяются компоненты вектора l0 [5,6].
(m = 1, 2, ј ; n = 0, 1, 2, ј ), т.е. при
любых начальных значениях игровая ситуация регулярна [7,8]. Получены уравнения,
из которых определяются компоненты вектора l0 [5,6].![]() - ограниченная величина, так как ряды, участвующие в выражениях (2.5), сходятся,
следовательно, оптимальные управляющие воздействия, определяемые формулой (2.4)
равномерно по t О [0,T],
составляют сходящиеся квадратом ряды [5,9]. Для определения момента J в каждой ситуации нужно найти наименьший корень уравнения
- ограниченная величина, так как ряды, участвующие в выражениях (2.5), сходятся,
следовательно, оптимальные управляющие воздействия, определяемые формулой (2.4)
равномерно по t О [0,T],
составляют сходящиеся квадратом ряды [5,9]. Для определения момента J в каждой ситуации нужно найти наименьший корень уравнения

![]() ,
,
![]() и
и
![]() (m = 1, 2, ј ; n = 0, 1, 2, ј ) трудно
представить в аналитической форме, то задачу решим численно.
(m = 1, 2, ј ; n = 0, 1, 2, ј ) трудно
представить в аналитической форме, то задачу решим численно.

![]() (m = 2, n = 0,1,2,3), а
следовательно вычислены гипотетическое рассогласование из (2.5), и оптимальные
управляющие воздействия из (2.4).
(m = 2, n = 0,1,2,3), а
следовательно вычислены гипотетическое рассогласование из (2.5), и оптимальные
управляющие воздействия из (2.4).![]() {t,0,30},
{t,0,30},
![]() {t,0,30} соответственно.
{t,0,30} соответственно.

![]() и
и
![]() имеют противоположные
знаки на том же интервале времени. Остальные оптимальные управляющие
воздействия,
имеют противоположные
знаки на том же интервале времени. Остальные оптимальные управляющие
воздействия,
![]() {t,0,30},
{t,0,30},
![]() {t,0,30}
(m = 2, n = 0,1,2) имеют тот же характер, что и
{t,0,30}
(m = 2, n = 0,1,2) имеют тот же характер, что и
![]() {t,0,30} (рис.2) и
{t,0,30} (рис.2) и
![]() {t,0,30} (рис. 3).
{t,0,30} (рис. 3).![]() (m = 2, n = 0,1,2,3), гасит колебательное
движение оболочки при самом упорном сопротивлении со стороны второго игрока
(m = 2, n = 0,1,2,3), гасит колебательное
движение оболочки при самом упорном сопротивлении со стороны второго игрока
![]() (m = 2, n = 0,1,2,3). А второй игрок,
наоборот, при (P < Q) может увеличить амплитуду колебаний.
(m = 2, n = 0,1,2,3). А второй игрок,
наоборот, при (P < Q) может увеличить амплитуду колебаний.