МАТЕМАТИКА
УДК 517.984.5
А. А. Асатрян
Исследование точечного спектра и обратной задачи рассеяния
для
оператора Штурма - Лиувилля с потенциалом, имеющим определенное
поведение на
бесконечности
(Представлено чл.-кор. НАН РА Г.Г. Геворкяном 15/VI 2005)
Ключевые слова: спектр,
обратная задача, дифференциальный оператор, данные рассеяния, собственная
функция
Рассмотрим на R = (-Ґ, Ґ)
дифференциальную операцию l, заданную формулой l(y) = -yўў + qy,
где коэффициент (потенциал) q - вещественная измеримая функция от переменной x
О R, удовлетворяющая условию
|
0
у
х
-Ґ
|
(1 - x)|q(x) - a-|dx + |
Ґ
у
х
0
|
(1 + x)|q(x) - a+|dx <
Ґ | |
с
некоторыми постоянными a± О R. Действующий в пространстве L2(R) оператор L
определим следующим образом (см. [1], с. 192). Область D определения оператора L
состоит из функций y О L2(R), имеющих
абсолютно непрерывные на каждом отрезке [a, b] М R первые производные и l(y)
О L2(R). Для y О D
по определению полагается Ly = l(y). Оператор L является самосопряженным (см.
[2]).
Обозначим m1 = min{a+, a-}, m2 = max{a+, a-}, m3 = Ґ.
Теорема 1. Собственные значения оператора L
(если таковые имеются) простые, лежат в
интервале (-Ґ, m1) и их число конечно.
В случае a+ = a- = 0 обратная задача рассеяния для оператора L
рассмотрена Л. Д. Фаддеевым (см. [3]; [4], с. 264-279), а при
a+ = a- №
0 легко приводится к указанному случаю. Поэтому мы будем считать a+
№ a-.
Обозначим
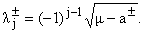 (m > m1; j = 1,2) (для корня берется главное
значение). Для m О R обозначим
через r±(m)
половину числа вещественных корней уравнения l2 + a± = m. Очевидно, что функции r+(m) и r-(m) постоянны в каждом интервале (mk, mk+1),
k = 1, 2. Для каждого k = 1, 2 обозначим через
(m > m1; j = 1,2) (для корня берется главное
значение). Для m О R обозначим
через r±(m)
половину числа вещественных корней уравнения l2 + a± = m. Очевидно, что функции r+(m) и r-(m) постоянны в каждом интервале (mk, mk+1),
k = 1, 2. Для каждого k = 1, 2 обозначим через 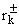 значение функции r±(m) в интервале (mk, mk+1).
значение функции r±(m) в интервале (mk, mk+1).
Для каждого k = 1,2 при m О (mk, mk+1)
уравнение l(j) = mj имеет k линейно независимых ограниченных решений jj(x, m) (x О R, 1 Ј j Ј k). Для этих решений справедливы асимптотические равенства
|
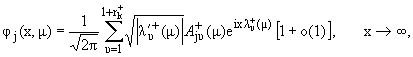
|
|
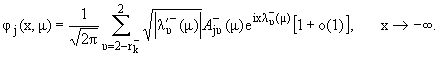
|
При
этом если обозначить
|
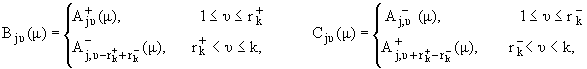
|
то
матрицы
|
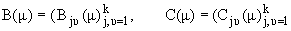
|
невырожденные
и связаны соотношением
В качестве одной из этих матриц
можно взять произвольную невырожденную матрицу, а по ней другая матрица и
решения jj(x,m)
определятся однозначно. Из (1) следует, что если одна из матриц B(m), C(m) унитарна, то другая тоже
унитарна. Впредь будем предполагать, что матрицы B(m),
C(m) унитарны, а их элементы измеримые функции (в
частности, в качестве одной из них можно взять единичную матрицу). При такой
нормировке систему решений jj(x,m) (m О
(mk,mk+1), 1 Ј j
Ј k) будем называть нормированной системой обобщенных
собственных функций оператора L, соответствующей значению m. При помощи jj(x,m) и собственных функций оператора L осуществляется
разложение Фурье (см. [5]).
Теперь, опираясь на асимптотическое поведение
обобщенных и обычных собственных функций, введем данные рассеяния для оператора
L.
Обозначим
|
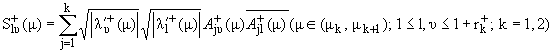 |
и рассмотрим матрицу
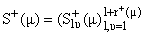 · S+(m) представляет собой квадратную матрицу порядка
1 + r+(m), которая не зависит от выбора
нормированной системы обобщенных собственных функций, причем матрица-функция
S+ непрерывно дифференцируема в интервалах (m1, m2) и
(m2, m3).
· S+(m) представляет собой квадратную матрицу порядка
1 + r+(m), которая не зависит от выбора
нормированной системы обобщенных собственных функций, причем матрица-функция
S+ непрерывно дифференцируема в интервалах (m1, m2) и
(m2, m3).
Обозначим через T точечный спектр оператора
L. Пусть m О T, а y - соответствующая нормированная собственная функция. Тогда
для y имеет место асимптотическое равенство
| y(x, m) = c+(m)eixl1+(m) [1 + o(1)], x ® Ґ, | |
где
c+(m) - ненулевое комплексное число.
Обозначим N+(m) = |c+(m)|2 (m О T). Легко видеть, что числа N+(m) не зависят от выбора нормированных собственных функций
y.
Рассмотрим набор данных
| {T, N+(m)(m О T), S+(m)(m О (m1, m2) И (m2, m3)) }, | |
(2) |
называемых правыми данными рассеяния
оператора L.
Обратная задача рассеяния для оператора L
состоит в восстановлении потенциала q по данным (2).
По аналогии работ [6, 7] с помощью данных
рассеяния введем функцию
|
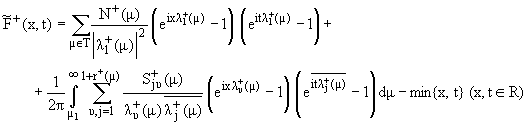 |
(интеграл
сходится в обычном смысле).
Сформулируем теорему, согласно которой
потенциал q определяется однозначно по данным рассеяния, и вопрос его
восстановления сводится к решению линейного интегрального уравнения.
Теорема 2. Существует непрерывная производная F+(x,t) = [(¶2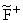 (x,t))/(¶x¶t)] (x,t О R), причем функция F+(x,t) вещественна и
симметрична (F+(x,t) = F+(t,x), x,t О R), а для каждого x О R линейное
интегральное уравнение
(x,t))/(¶x¶t)] (x,t О R), причем функция F+(x,t) вещественна и
симметрична (F+(x,t) = F+(t,x), x,t О R), а для каждого x О R линейное
интегральное уравнение
| K+(x,t) + F+(x,t) + |
Ґ
у
х
z
|
K+(x,x)F+(x,t)dx = 0 (t
О [x,Ґ)) | |
имеет
единственное решение K+(x, ·) в любом из классов Lp(x,Ґ), 1 Ј p Ј
Ґ и имеют место равенства
| a+ = |
lim
m ®Ґ
|
|
й
к
л |
m - |
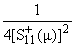 |
щ
ъ
ы |
, | |
| q(x) = a+ - 2 |
d
dx
|
K+(x,x), x О
R. | |
Автор приносит глубокую благодарность профессору И. Г. Хачатряну за
постановку задачи и полезные обсуждения результатов.
Ереванский государственный университет
Литература
1. Наймарк М. А. Линейные дифференциальные операторы. М. Наука.
1969.
2. Петросян А. Г.
- Уч. зап. ЕГУ. 2003. N 3. С.
8-15.
3. Фаддеев Л. Д.
- Труды Мат. ин-та АН СССР. 1964. Т. 73. С.
314-336.
4. Марченко В. А.
Операторы Штурма-Лиувилля и их приложения. Киев. Наукова
думка. 1977.
5. Петросян А. Г.,
Хачатрян И. Г. - Уч. зап. ЕГУ. 2004. N 1. С.
22-27.
6. Хачатрян И. Г.
- Изв. АН Арм. ССР. Математика. 1983. Т. 18. N 5. С.
394-402.
7. Бабасян С. В.
- Уч. зап. ЕГУ. 1989. N 3 (171).
![]() (m > m1; j = 1,2) (для корня берется главное
значение). Для m О R обозначим
через r±(m)
половину числа вещественных корней уравнения l2 + a± = m. Очевидно, что функции r+(m) и r-(m) постоянны в каждом интервале (mk, mk+1),
k = 1, 2. Для каждого k = 1, 2 обозначим через
(m > m1; j = 1,2) (для корня берется главное
значение). Для m О R обозначим
через r±(m)
половину числа вещественных корней уравнения l2 + a± = m. Очевидно, что функции r+(m) и r-(m) постоянны в каждом интервале (mk, mk+1),
k = 1, 2. Для каждого k = 1, 2 обозначим через ![]() значение функции r±(m) в интервале (mk, mk+1).
значение функции r±(m) в интервале (mk, mk+1).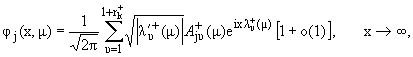
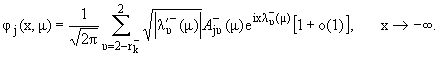
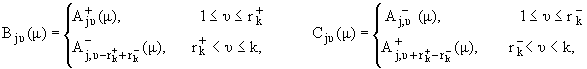
![]()
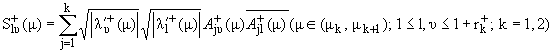
![]() · S+(m) представляет собой квадратную матрицу порядка
1 + r+(m), которая не зависит от выбора
нормированной системы обобщенных собственных функций, причем матрица-функция
S+ непрерывно дифференцируема в интервалах (m1, m2) и
(m2, m3).
· S+(m) представляет собой квадратную матрицу порядка
1 + r+(m), которая не зависит от выбора
нормированной системы обобщенных собственных функций, причем матрица-функция
S+ непрерывно дифференцируема в интервалах (m1, m2) и
(m2, m3).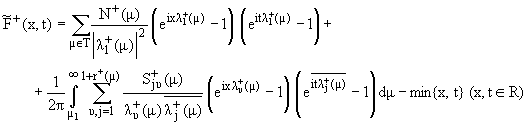
![]() (x,t))/(¶x¶t)] (x,t О R), причем функция F+(x,t) вещественна и
симметрична (F+(x,t) = F+(t,x), x,t О R), а для каждого x О R линейное
интегральное уравнение
(x,t))/(¶x¶t)] (x,t О R), причем функция F+(x,t) вещественна и
симметрична (F+(x,t) = F+(t,x), x,t О R), а для каждого x О R линейное
интегральное уравнение ![]()