МАТЕМАТИКА

УДК 517.53

Академик В. С. Захарян, М. М. Мирзоян

Предельные множества эквиморфных функций по произвольным
касательным направлениям

(Представлено 6/V 2005)

   Ключевые слова: предельные множества, эквиморфные функции, эквиморфизм, P-последовательность

   В настоящей работе продолжено изучение граничных свойств эквиморфных в единичном круге функций [1] вдоль произвольных касательных путей (см. [2]); используются все содержащиеся там обозначения и определения.
   1. Пусть D : |z < 1 - единичный круг, G : |z| = 1 - единичная окружность, W - сфера Римана. Х.Э. Мехия функцию f : D ® W называет эквиморфной функцией, если f есть композиция f(z) = g(h(z)) некоторой мероморфной функции g(z) в круге D и эквиморфизма h : D ® D, т.е такого гомеоморфизма круга D на себя, что h, h-1 равномерно непрерывны относительно гиперболической метрики единичного круга [1].
   Пусть x = eiq О G. Для произвольных действительных чисел a и q, 0 < a < Ґ, q і 0 назовем правым q-путем L+(x, q, a) всякую кривую, которая задается непрерывной на [0;1) функцией z = z(t) со свойствами:
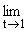      z(t) = x; |z(t) - x| < [1/2]; q < argz(t) < q + [(p)/6], argz(t) ® q (монотонно), при t ® 1 и
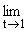       (1 - |z(t)|)|argz(t) - q|-q-1 = a.

   Назовем правым q*-путем L+(x,q*,a) правый q-путь, задающийся уравнением
z = [1 - a(j - q)q+1] · eij,    j О (q;q + a-[1/(1+q)]].

   Обозначим через L-(x, q, a) (L- (x, q*, a)), 0 < a < Ґ, q і 0 и назовем левым q-путем (q*-путем) oбрaз правого q-пути L+(x, q, a) (L+(x, q*, a)) при симметрии относительно радиуса h(x,0) круга D в точке x = etj О G. Правые и левые q-пути (q*-пути) назовем q-путями (q*-путями) L(x, q, a) (L(x, q*, a)) или просто L(x, q) (L(x, q*)).
   Для произвольных a > 0, b > 0, q1 і 0, q2 і 0, 0 < d < [1/2] назовем (q1,q2)-углом ((q1,q2)*) в точке x О G и обозначим через D(x,q1,q2,a,b,d) (D*(x,q1,q2,a,b,d)) или просто D(x,q1,q2) (D*(x,q1,q2,)), если нас не интересуют размеры этого угла, подобласть круга D, ограниченную двумя разными L(x,q1,a)  (L(x,q1*,a)) и L(x,q2,b)  (L(x,q2*,b)) путями (возможен случай q1 = q2) и окружностью |z - x| = d, где d достаточно малое положительное число.
   2. Для произвольной f : D ® W, произвольной точки x О G и произвольного множества S М D, для которого x является предельной точкой, предельное множество C(f, x, S) определяется как пересечение
C(f, x, S) =
З
r > 0 
f(Vr(x)ЗS)
 
 ,  где Vr(x) = {z О D;| к
к 		z - x к
к 		< r}, r > 0,

черта - замыкание множества.
   Пусть A - произвольное конечное множество неотрицательных чисел. Для произвольной f : D ® W точку x О G отнесем к множеству MA(f), если для произвольного q-пути L(x,q), q О A, имеем C(f,x,L(x,q)) = C(f,x,D) № W. Точку x О G отнесeм к множеству IA(f), если для произвольного (q1,q2)-угла D(x,q1,q2), q1,q2 О A имеем C(f,x,D(x,q1,q2)) = W. Точку x О G отнесем к множеству PA(f), если каждый q-путь L(x,q) содержит P-последовательность [3,4] функции f(z). Точку x О G отнесем к множеству EA(f), если для любого (q1,q2)-угла D(x,q1,q2), q1,q2 О A, справeдливо C(f,x,D(x,q1,q2)) = C(f,x,D). Tочку x О G отнесем к множеству I*A(f), если для любого q-пути L(x,q), q О A, имеем C(f ,x, L(x, q)) = W и каждый q-путь L(x,q), q О A не содержит ни одной P-последовательности функции f(z). Ясно, что I*A(f) М IA(f).
   Справедлива следующая теорема, которая является усилением теоремы 1 из [5].
   Теорема 1. Для произвольной эквиморфной в круге D функции f : D ® W и для произвольного конечного множества A неотрицательных чисел справедливо разложение
G = MA(f) И I*A(f) И PA(f) И F,

где F - множество первой категории на G.
   Докaзательство. Пусть эквиморфная в D функция f(z) имеет каноническое представление f = g(h(z)) и пусть Qf(z) = (1 - |h(z)|2) · |gў(h(z))| · (1 + |g(h(z))|2)-1.
   Применим теорему 3 из [2] к функциям f(z) и Qf(z). Получим следующие разложения:
G = EA(f) И F1,    G = EA(Qf) И F2,

где F1 и F2 - множества первой категории на G. Следовательно, дополнение множества RA(f) = EA(f) З EA(Qf) имеет первую категорию на G. Покажем, что справедливо вложение RA(f) М MA(f) И I*A(f) И PA(f).
   Действительно, в произвольной точке x О RA(f) имеем следующие четыре возможности:
I. множество C(Qf, x, D) ограничено и C(f, x, D) № W;
II. множество C(Qf, x, D) ограничено и C(f, x, D) = W;
III. множество C(Qf, x, D) не ограничено и C(f, x, D) = W;
IV. множество C(Qf, x, D) не ограничено и C(f, x, D) № W.
   Если x О RA(f) и C(Qf, x, D) ограничено, то согласно теореме 2 из [2] для каждого q-пути L(x, q), q О A, в точке x справедливо
C(f, x, L(x, q)) = C(f, x, D).

   Поэтому в случае реализации возможности I, имеем x О MA(f). Если реализуется возможность II, то согласно теоремам 1 и 2 из [2] имеем x О I*A(f). Если x О RA(f) и C(Qf, x, D) не ограничено, то каждый q-путь L(x, q), q О A, содержит P-последовательность функции f(z). Следовательно, возможность IV не может реализоваться, а при реализации возможности III имеем x О PA(f).
   Теорема 1 полностью доказана.
   Замечание. В случае, когда A = {0} и f - эквиморфная в D функция, теорема 1 доказана в работе [1], в случае, когда f - мероморфная в D функция, она усиливает теорему 1 из [7], в случае, когда A = { 0;1} и f - мероморфная в D функция, она усиливает теорему 1 из [8]. В топологических пространствах сходные теоремы доказаны в работах [9-11].
   Из теоремы 4 из [2] и теоремы 1 следует
   Теорема 2. Для произвольной эквиморфной в круге D функции f : D ® W и для произвольного конечного множества A неотрицательных чисел справедливо разложение
IA(f) = I*A(f) И PA(f) И F,

где F - множество первой категории.
   Замечание. В случае, когда f - мероморфная в D функция, теорема 2 усиливает теорему 2 из [7], в случае, когда A = {0} и f - мероморфная в D функция, она доказана в [12].
   4. Справедлива следующая теорема.
   Теорема 3. Для произвольной эквиморфной в круге D функции f : D ® W и для произвольного конечного множества A неотрицательных чисел множество PA(f) имеет тип Gd на G.
   Доказательство. Обозначим через B = {aj, bk} последовательность всех положительных рациональных пар (aj, bk), aj > 0, bk > 0 и будем считать A = { qi}, qi і 0. Пусть (aj, bk) О B, qi О A, qr О A и n и m, n = 1,2,ј, m = 2,3,ј, произвольные фиксированные числа. Обозначим через En,m,j,k,i,r - множество таких точек x О G, для которых
Sup
 [Qf (z)] Ј n,
z О D*(x, qi, qr, aj, bk, 1
m
 ).
   Покажем, что справедливо разложение:
G\PA(f) = ИEn,m,j,k,i,r.
 (1)

   Поскольку вложение ИEn,m,j,k,i,r М G\PA(f) очевидно, то для доказательства обратного вложения допустим, что x произвольная точка множества G\PA(f). Тогда согласно теореме 1 из [2] можно найти (q1,q2)-угол D(x,q1,q2), q1,q2 О A, в котором C(Qf,x,D(x,q1,q2)) ограничено. Следовательно, можно найти такое натуральное число n О N и такой (qi, qr)*-угол D*(x, qi, qr, aj, bk, [1/m]) М D(x, qi, qr, aj, bk, [1/m]), qi, qr О A, (aj, bk) О B, m > 2, m О N, при которых в точке x имеем

Sup
 [Qf(z)] Ј n,
z О D*(x, qi, qr, aj, bk, 1
m
 ),
т.е. x О En,m,j,k,i,r. Чтобы доказать, что каждое множество En,m,j,k,i,r из (1) замкнуто, допустим, что x0 О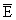n,m,j,k,i,r. Поскольку
D*(x0, qi, qr, aj, bk, 1
m
 ) М
И
x О En,m,j,k,i,r 
 D* (x, qi, qr, aj, bk, 1
m
 ),

то множества En,m,j,k,i,r замкнуты и теорема 3 доказана.
   Замечание. В случае, когда A = {0} и f - эквиморфная в D функция, теорема 3 доказана в [1], в случае, когда f - мероморфная в D функция, она усиливает теорему 3 из [7], в случае A = {0} и f - мероморфная в D функция, она доказана в [12].
   4. Справедлива следующая
   Теорема 4. Для произвольной эквиморфной в D функции f : D ® W и для произвольного конечного множества A неотрицательных чисел множество MA(f) имеет структуру MA(f) = G \F, где G М G открытое множество, а F - множество первой категории и типа Fs на G.
   Доказательство. Обозначим через K(f) множество таких точек x О G, для которых C(f, x, D) № W. По определению K(f) - открытое множество. Докажем справедливость равенства
MA(f) = EA(f) З K(f).

   Действительно, вложение MA(f) М EA(f) З K(f) следует из определений участвующих в нем множеств. Обратное вложение следует на основании теоремы 2 из [2]. Заменяя теперь множество EA(f) разностью G\F (см. теорему 3 из [2]), где F - множество первой категории и типа Fs, получим утверждение теоремы 4.
   Замечание. В случае, когда A = {0} и f - эквиморфная в D функция, теорема 4 установлена в [1], в случае, когда f - мероморфная в D функция, она усиливает теорему 5 из [7], в случае, когда A = {0} и f - мероморфная в D функция, она доказана в [12].

     Государственный инженерный университет Армении

Литература

     1. Мехия Х.Э.  - ДАН СССР. 1982. T. 265. N1. C. 35-38.
     2. Мирзоян М.М.  - ДНАН Армении. 2005. Т. 105. N4. С. 328-332.
     3. Гаврилов В.И.  - Матем. сб. 1965. T. 67 (109). N3. C. 408-427.
     4. Гаврилов В.И.  - Матем. сб. 1966. T. 71 (113). N3. C. 386-404.
     5. Гаврилов В.И.  - ДАН СССР. 1974. T. 216. N1. C. 21-23.
     6. Мирзоян М.М.  - ДАН АрмССР. 1978. T. 66. N4. C. 200-204.
     7. Мирзоян М.М.  - ДАН АрмССР. 1978. T. 66. N5. C. 263-266.
     8. Айрапетян А.Н., Гаврилов В.И.  - Изв. АН АрмССР. 1976. Математика. Т. 11. N5. C. 390-399.
     9. Эминян О.М.  - ДАН АрмССР. 1988. T. 86. N1. C. 3-7.
     10. Симушев А.А.  - ДАН СССР. 1986. T. 289. N2. C. 305-309.
     11. Абду Аль-Рахман Хасан.  - ДАН СССР. 1981. T. 260. N4. C. 777-780.
     12. Гаврилов В.И.  - ДАН СССР. 1977. T. 232. N6. C. 1237-1240.