МАТЕМАТИКА
УДК 517.58
А. В. Погосян
Об одной линейной рационально-тригонометрической
интерполяции
гладких функций
(Представлено академиком А.Б. Нерсесяном 11/III 2005)
Ключевые слова: тригонометрическая интерполяция, рациональная аппроксимация, минимизация
ошибки
1. Восстановление
гладкой на конечном отрезке [-1,1] функции f по ее
коэффициентам Фурье [1]
| fn = |
1
2
|
у1
х-1 |
f(x)e-ipn xdx, n = 0, ±1, ±2, ј ±N, N і 1 | |
(1) |
или по дискретным коэффициентам
Фурье [2,3]
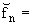 |
1
2N+1
|
|
N
е
k=-N
|
f(xk)e-ipn
xk, xk = |
2k
2N+1
|
, |n| Ј N, N і
1 | |
(2) |
практически неэффективно, если
разлагаемая функция, продолженная на всю числовую ось 2-периодически, не
обладает достаточной гладкостью.
Одним из методов ускорения сходимости рядов
Фурье является нелинейный алгоритм Фурье - Паде [4,5].
В настоящей работе предлагается линейный
метод ускорения сходимости классической тригонометрической интерполяции, также
основанный на идее метода Паде. Для дополнительного ускорения сходимости
применяется так называемая "полная интерполяция" [6]. Изучается
L2-сходимость полученных параметрических интерполяций. Решается
задача минимизации L2-ошибки с нахождением оптимальных значений
параметров.
Рассмотрим формулу
f(x) »
IN(f, x, q) =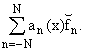 |
|
(3) |
Для определения функций
an(x) потребуем, чтобы формула (3) была точной для системы
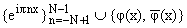 , где
, где
| j(x) = eipNx - q |
eip(N+1)x
1 + qeipx
|
, -1 < q <
1. | |
(4) |
После несложных вычислений получим
| IN(f, x, q) = |
N
е
n=-N
|
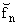 eipnx + q eipnx + q |
e-ipNx - eip(N+1)x
1 + 2qcospx + q2
|
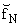 + q + q |
eipNx - e-ip(N+1)x
1 + 2qcospx + q2
|
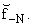 | |
(5) |
Заметим, что выражение
| IN(f, x, 0) = |
N
е
n=-N
|
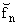 eipnx eipnx | |
(6) |
является классической
тригонометрической интерполяцией.
Теорема 1. Для f О C[-1,1] и любого -1 < q < 1 формула (5)
интерполяционная на сети
{xk} (см. (2)), т.е.
| IN(f, xk, q) = f(xk), |k| Ј N. | |
(7) |
Доказательство проводится прямой проверкой.
2. Через || · || обозначим норму в пространстве L2(-1,1)
| ||f|| = |
ж
и |
у1
х-1 |
|f(x)|2dx |
ц
ш |
1/2
|
| |
и
для f О Cq[-1,1]
обозначим Ak(f) = f (k)(1) - f (k)(-1),
k = 0, ј , q. Далее
| Fq(x) = |
Ґ
е ¢
s=-Ґ
|
(-1)s
(x + s)q+1
|
, |x| Ј |
1
2
|
, q і
0, | |
где штрих у знака суммы
означает, что нулевой член отсутствует. Заметим, что
| F0(x) = |
px - sinpx
xsinpx
|
и Fq(x) = |
(-1)q
q!
|
F0(q)(x). | |
Оценим асимптотическое поведение ошибки
RN(f, x, q) = f(x) - IN(f, x, q) в
L2-метрике. Сначала изучим случай q = 0.
Теорема 2. Пусть f О Cq[-1,1],
f (q+1) О L1[-1,1], q і 1 и Aj(f) = 0
для j = 0, ј , q - 1.
Тогда
|
lim
N®Ґ
|
(2N + 1)q+[1/2]||RN(f, x, 0)|| = cq|Aq(f)|, | |
(8) |
| cq = |
1
pq+1
|
|
ж
з
и |
22q+1
2q+1
|
+ |
у
х |
1/2
0
|
Fq2(x)dx |
ц
ч
ш |
1/2
|
. | |
Доказательство непосредственно следует из
известного асимптотического разложения коэффициентов Фурье
| fn = |
(-1)n+1
2
|
|
Aq(f)
(ipn)q+1
|
+ |
1
2(ipn)q+1
|
|
у1
х-1 |
f (q+1)(x)e-ipnxdx, | |
(9) |
с учетом формулы
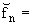 |
Ґ
е
s=-Ґ
|
fn+s(2N+1), |n| Ј N. | |
(10) |
Рассмотрим теперь случай q № 0.
Теорема 3. Пусть f О Cq+1[-1,1],
f (q+2) О L1[-1,1], q і 1 и Aj(f) = 0,
j = 0, ј , q - 1. Тогда для
имеет место следующая
асимптотическая оценка:
|
lim
N®Ґ
|
(2N+1)q+[1/2]||RN(f, x, q)|| = cq,t|Aq(f)|, | |
(12) |
где для четныx значений q
| cq,t = |
1
pq+1
|
|
ж
з
и |
|
у
х |
Ґ
1/2
|
|
к
к
к |
1
xq+1
|
- e-2txch(t)(Fq(1/2) + 2q+1) |
к
к
к |
2
|
+ | |
| + |
у
х |
1/2
0
|
|Fq(x) - e-t sh(2tx)(Fq(1/2) + 2q+1)|2 |
ц
ч
ш |
1/2
|
| |
и
для нечетных значений q
| cq,t = |
1
pq+1
|
|
ж
з
и |
|
у
х |
Ґ
1/2
|
|
к
к
к |
1
xq+1
|
- e-2txch(t) |
q+1
2t
|
(Fq+1(1/2) + 2q+2) |
к
к
к |
2
|
+ | |
| + |
у
х |
1/2
0
|
|
к
к
к |
Fq(x) + e-tch(2tx) |
q+1
2t
|
(Fq+1(1/2) + 2q+2) |
к
к
к |
2
|
|
ц
ч
ш |
1/2
|
. | |
Доказательство. Для N > t имеем
| ||RN(f, x, q)|| = 2 |
N-1
е
n=-N+1
|
|
к
к
к |
fn -
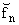 - (-1)n+N - (-1)n+N |
q N+1
1 - q2
|
(qnDN(q) + q-nD-N(q)) |
к
к
к |
2
|
+ | |
| + 2 |
Ґ
е
n=N
|
|
к
к
к |
fn - (-1)n+N |
qn
1 - q2
|
DN(q)(qN+1 + q-N) |
к
к
к |
2
|
+ | |
| + 2 |
-N
е
n=-Ґ
|
|
к
к
к |
fn - (-1)n+N |
q-n
1 - q2
|
D-N(q)(qN+1 + q-N) |
к
к
к |
2
|
, | |
(13) |
где
DN(q) =
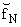 + q + q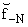 и
D-N(q) = и
D-N(q) =
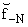 + q + q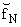 . . | |
С учетом (10) и (9) получим (N ® Ґ)
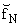 = = |
Aq(f)(-1)N
2(ip)q+1
|
|
ж
з
и |
z(q)
Nq+1
|
- |
q + 1
2
|
z(q) - z(q + 1)
Nq+2
|
ц
ч
ш |
+ |
Aq+1(f)(-1)N
2(ip)q+2
|
|
z(q + 1)
Nq+2
|
+ o(N-q-2). | |
Отсюда
для четных q имеем
| DN(q) = |
Aq(f)(q + 1)(-1)N+1
2(2N + 1)q+2(ip)q+1
|
z(q + 1) + o(N-q-2), N ® Ґ, D-N(q) = DN(q) | |
(14) |
и для нечетных
| DN(q) = |
Aq(f)(-1)N+1t
(2N + 1)q+2(ip)q+1
|
z(q) + o(N-q-2), N ® Ґ, D-N(q) = -DN(q). | |
(15) |
Подставляя (14), (15) в (13), получим требуемое.
Абсолютные константы cq и
cq,t в теоремах 2, 3 характеризуют
сходимость IN(f, x, q) по норме || · ||. Заметим, что константа cq,t зависит от t и естественно
ее минимизировать. Соответствующие результаты, с точностью до 3 знаков после
запятой, представлены в табл. 1. Отношение cq/cq,t характеризует коэффициент эффективности оптимальной
интерполяции по сравнению с классической.
Таблица
1
Приближенные значения констант cq и
cq,t
при оптимальном значении параметра
t
| q |
1 |
2 |
3 |
4 |
5 |
6 |
| cq |
0.2372 |
0.1074 |
0.0627 |
0.0345 |
0.0201 |
0.0117 |
| cq,t |
0.0434 |
0.0122 |
0.0079 |
0.0019 |
0.0017 |
0.0005 |
| t |
1.8081 |
2.4581 |
3.7303 |
4.3705 |
5.7525 |
6.2959 |
| cq/cq,t
|
5.5 |
8.8 |
7.9 |
18.1 |
11.8 |
23.4 |
Рассмотрим следующий пример:
| f(x) = (1 - x2)2sin(33 x - 0.5). | |
(16) |
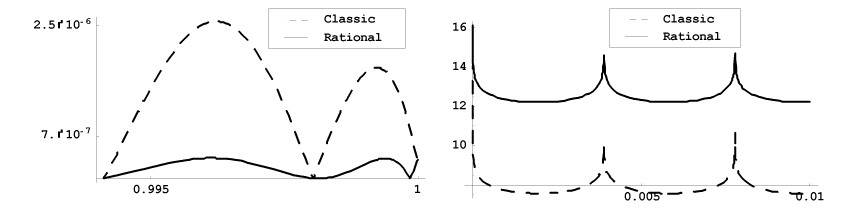
На рис. 1 показано сравнение результатов
аппроксимации функции (16)
классической тригонометрической интерполяцией и оптимальной рациональной
интерполяцией. Оптимальные значения параметра t выбраны
согласно табл. 1.
Рис. 1. Графики функций |RN(f, x, 0)|-(Classic), |RN(f, x, q)|-(Rational) в
окрестности точки x = 1 (слева) и -log10|RN(f, x, 0)|, -log10|RN(f, x, q)| в
интервале [0,0.01] (справа) для N = 256.
3. Заметим теперь, что в
интерполяции IN(f, x, q) используются значения
функции f только в интервале [2N/(2N + 1),2N/(2N + 1)] и
ошибка аппроксимации максимальна вблизи концов отрезка. Для уменьшения этой
ошибки можно, следуя подходу работы [6] к функции
| f*(x) = f |
ж
з
и |
|
2N + 1
2N
|
x |
ц
ч
ш |
, x О
[- |
2N
2N + 1
|
, |
2N
2N + 1
|
], | |
применить
интерполяцию IN(f*, x, q), где
значения f*(x) при [-(2N + 1)/2N,-1], [1,(2N + 1)/2N] не используются. Сделав обратную замену,
получим так называемую полную интерполяцию IN*(f, x, q) на сети xk* = [k/N]
IN*(f, x, q) =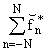 eipn
[2N/(2N+1)]x + eipn
[2N/(2N+1)]x + |
|
| + q |
e-ipN[2N/(2N+1)]x - eip(N+1)[2N/(2N+1)]x
| 1 + 2qcosp |
2N
2N+1
|
x + q2 | |
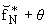 |
eipN[2N/(2N+1)]x - e-ip(N+1)[2N/(2N+1)]x
| 1 + 2qcosp |
2N
2N+1
|
x + q2 | |
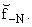 | |
(17) |
Рассмотрим асимптотическое поведение ошибки
RN*(f, x, q) = f(x) - IN*(f, x, q) по
метрике || · ||. Доказательство следующих двух
теорем непосредственно следует из легко проверяемой формулы
| ||RN*(f, x, q)||2 = |
2N + 1
2N
|
||RN(f*, x, q)||2 - |
1
2N
|
|
у
х |
1
0
|
|
к
к
к |
RN |
ж
з
и |
f*,1 - |
h
2N + 1
|
, q |
ц
ч
ш |
к
к
к |
2
|
dh - | |
| - |
1
2N
|
|
у
х |
1
0
|
|
к
к
к |
RN |
ж
з
и |
f*, -1 - |
h
2N + 1
|
, q |
ц
ч
ш |
к
к
к |
2
|
dh. | |
Теорема 4. Пусть
f О Cq[-1,1],
f (q+1) О L1[-1,1], q і 1 и Aj(f) = 0,
j = 0, ј , q - 1. Тогда имеет место
формула
|
lim
N®Ґ
|
(2N + 1)q+[1/2]||RN*(f, x, 0)|| = cq*|Aq(f)|, | |
(18) |
где
| cq* = |
ж
и |
cq2 - 2 |
у
х |
1
0
|
|lq(h)|2dh |
ц
ш |
1/2
|
, | |
| lq(h) = |
1
pq+1
|
|
у
х |
1/2
0
|
sinp |
ж
з
и |
xh + |
q
2
|
ц
ч
ш |
|
Ґ
е
¢
s=-Ґ
|
(-1)s
(x + s)q+1
|
dx - |
1
pq+1
|
|
у
х |
Ґ
1/2
|
|
xq+1
|
dx. | |
Теорема 5. Пусть
f О Cq+1[-1,1],
f (q+2) О L1[-1,1], q і 1 и Aj(f) = 0,
j = 0, ј , q - 1. Тогда для
имеет место формула
|
lim
N®Ґ
|
(2N + 1)q+[1/2]||RN*(f, x, q)|| =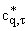 |Aq(f)|, |Aq(f)|, | |
(20) |
где
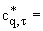 |
ж
и |
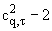 |
у
х |
1
0
|
|lq,t(h)|2dh |
ц
ш |
1/2
|
| |
и
для четных q
| lq,t(h) = lq(h) + (-1)q/2 |
hcos(ph/2)
pq(4t2 + p2 h2)
|
z(q), | |
для
нечетных q
| lq,t(h) = lq(h) - (-1)[(q+1)/2] |
(q + 1)cos(ph/2)
pq+1(4t2 + p2 h2)
|
z(q + 1). | |
Здесь также параметр t определяется из условия минимизации константы
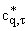 . Соответствующие результаты представлены
в табл. 2. Отношение cq/cq* показывает
эффективность полной интерполяции по сравнению с классической интерполяцией, а
отношение cq,tў /
. Соответствующие результаты представлены
в табл. 2. Отношение cq/cq* показывает
эффективность полной интерполяции по сравнению с классической интерполяцией, а
отношение cq,tў /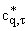 показывает эффективность полной рациональной интерполяции по сравнению с
рациональной, где tў выбран
согласно табл. 1. Как видим, полная интерполяция эффективна при q Ј 3.
показывает эффективность полной рациональной интерполяции по сравнению с
рациональной, где tў выбран
согласно табл. 1. Как видим, полная интерполяция эффективна при q Ј 3.
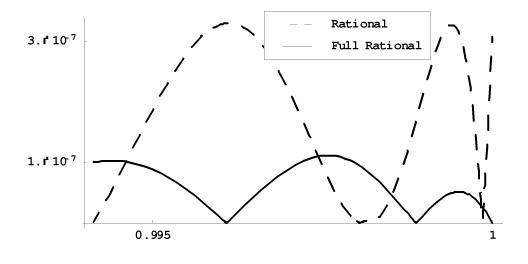
На рис. 2 показаны результаты аппроксимации
функции (16) посредством
рациональной и полной рациональной интерполяций.
Таблица
2
Приближенные значения констант cq* и
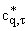 для
для
оптимальных t. Параметр tў взят согласно табл. 1
| q |
1 |
2 |
3 |
4 |
5 |
6 |
| cq* |
0.0737 |
0.1031 |
0.0383 |
0.0342 |
0.0154 |
0.0117 |
| cq / cq* |
3.2 |
1.04 |
1.63 |
1.007 |
1.3 |
1.002 |
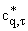 |
0.0032 |
0.0036 |
0.0019 |
0.0015 |
0.0008 |
0.0005 |
| t |
2.6540 |
2.7268 |
4.2723 |
4.4243 |
6.0581 |
6.3139 |
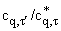 |
13.6 |
3.4 |
4.1 |
1.3 |
1.9 |
1 |
Рис. 2. |RN(f, x, q)| и
RN*(f, x, q)| для N = 256 с оптимальными
параметрами q = 1 - [(t)/N], взятыми из табл. 1, 2.
Из приведенных и многих других
экспериментальных результатов следует, что рациональная интерполяция значительно
более эффективна по сравнению с классической, а при q Ј
3 полная интерполяция еще более эффективна.
В заключение отметим, что оптимальные
значения параметра t в табл. 1 и 2 получены применением
системы MATHEMATICA [7].
Работа выполнена в рамках проекта ISTC A-823.
Институт математики НАН РА
Литература
1. Zygmund A. Trigonometric Series. 1959. V. 1. Cambridge Univ. Press.
2. Nersessian A.
Theory of functions and applications. Collection of Works
Dedicated to the Memory of Mkhitar M. Djrbashian. "Louys" Publishing House.
1995. P. 133-138.
3. Nersessian A., Hovhannisian N. - Journal of
contemporary mathematical analysis. Matematika. 2002. V. 37. N 5. P.
48-62.
4. Бейкер Дж.,
Грейвс-Моррис П. Аппроксимации Паде. М. Мир. 1986. 502
с.
5. Geer J. - Journal of Scientific Computing. 1995. V. 10. N. 3. P.
325-356.
6. Нерсесян А. Б.,
Оганесян Н. В. - ДНАН Армении. 2001. T. 101. N 2.
С. 12-15.
7. Wolfram S.
The MATHEMATICA book. Fourth Edition, Wolfram Media. 1999.
Cambridge University Press.
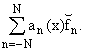
![]() , где
, где ![]() eipnx + q
eipnx + q![]() + q
+ q![]()
![]() eipnx
eipnx![]()
![]() - (-1)n+N
- (-1)n+N![]() + q
+ q![]() и
D-N(q) =
и
D-N(q) =
![]() + q
+ q![]() .
.![]() =
= 
![]() eipn
[2N/(2N+1)]x +
eipn
[2N/(2N+1)]x +![]()
![]()
![]() |Aq(f)|,
|Aq(f)|,![]()
![]()
![]() . Соответствующие результаты представлены
в табл. 2. Отношение cq/cq* показывает
эффективность полной интерполяции по сравнению с классической интерполяцией, а
отношение cq,tў /
. Соответствующие результаты представлены
в табл. 2. Отношение cq/cq* показывает
эффективность полной интерполяции по сравнению с классической интерполяцией, а
отношение cq,tў /![]() показывает эффективность полной рациональной интерполяции по сравнению с
рациональной, где tў выбран
согласно табл. 1. Как видим, полная интерполяция эффективна при q Ј 3.
показывает эффективность полной рациональной интерполяции по сравнению с
рациональной, где tў выбран
согласно табл. 1. Как видим, полная интерполяция эффективна при q Ј 3.![]() для
для ![]()
![]()