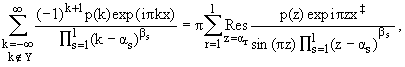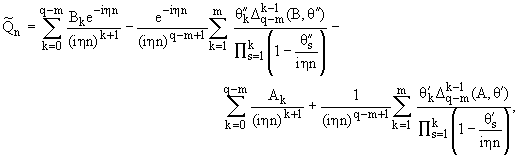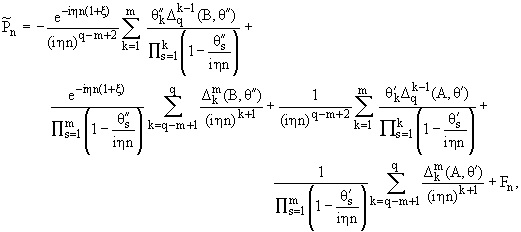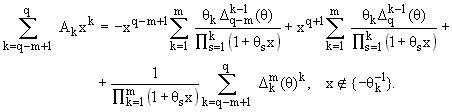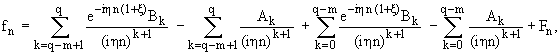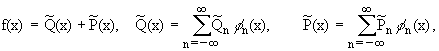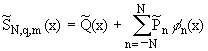МАТЕМАТИКА
УДК 517.518
Академик А. Б. Нерсесян, Р. Г. Бархударян
Ускорение сходимости разложения по собственным функциям
одной
модельной краевой задачи с разрывным коэффициентом
(Представлено 15/VI 2005)
Ключевые слова: краевые задачи, ускоренная сходимость,
разложения по собственным функциям
1.
Введение. Хорошо известно, что классический ряд Фурье на отрезке [a,b],
-Ґ < a < b < Ґ, сходится медленно, если разлагаемая функция f(x),
продолженная на всю действительную ось (b - a)-периодически, не обладает достаточной гладкостью. Это
прежде всего относится к кусочно-гладким функциям.
Решение практически
важной проблемы ускорения сходимости разложений таких функций в ряд Фурье, -
по-видимому, впервые, - предложил А. Крылов в 1907 г. (см. [1]). Начало
систематическому обоснованию такого подхода положила в 1964 г. работа Ланцоша
[2] (см. также [3-7]). Практически эффективные алгоритмы были разработаны за
последние 15 лет главным образом в работах К. Экгофа и Д. Готтлиба с соавторами
(см., например, [8,9]). Этот подход (алгоритм) назовём КЕГ-методом.
В работе [13] был разработан другой, нелинейный метод ускорения
сходимости рядов Фурье, основанный на применении аппроксимантов Паде к асимптотическому
ряду коэффициентов, что привело к еще более точным и устойчивым алгоритмам
(квазиполиномиальный (QP) метод). К тому же стало возможным эффективно выявлять
колебания произвольной частоты (в том числе затухающие или нарастающие),
являющиеся "скрытыми" компонентами разлагаемой функции.
Ниже приводятся некоторые теоретические оценки и явные формулы,
связанные с последним подходом, в применении к краевой задаче для простейшего
дифференциального уравнения с разрывным коэффициентом.
Отметим, что изучению
задач подобного типа, - с точки зрения вычисления собственных значений и
собственных функций, - посвящена работа [4].
2. Постановка задачи. Рассмотрим краевую задачу
где x О (-1,1),
b О R+
Легко видеть, что собственные значения этой задачи
имеют явный вид lk = -phk, где k
О Z и h = [(2p)/(1+x+b2(1-x))], а система собственных функций
{fn} следующая:
Система собственных функций сопряженной задачи имеет вид
Введем обозначения
| Ak = |
f (k)(1)
b2k
|
- f (k)(-1), Bk = |
f (k)(x + 0)
b2k
|
- f (k)(x - 0), | |
(6) |
Лемма 1. Пусть f О Cq+1
на каждом из отрезков
[-1,x],[x,1]. Тогда
| fn = |
q
е
k=0
|
|
e-ihn(1+x)Bk
(ihn)k+1
|
- |
q
е
k=0
|
|
Ak
(ihn)k+1
|
+ Fn, | |
(7) |
где
| Fn = |
1
(ihn)(q+1)
|
|
|
у
х |
1
-1
|
|
f q+1(x)
e(x,x)(q+1)
|
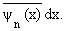 |
|
(8) |
Доказательство.
|
| fn = (f, yn) = |
у
х |
1
-1
|
f(x) |
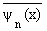 |
dt = |
у
х |
x
-1
|
f(x) |
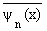 |
dx + |
у
х |
1
x
|
f(x) |
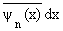 |
= | |
|
(9) |
|
|
у
х |
x
-1
|
f(x)e-ih(1+x)dx + b2 |
у
х |
1
x
|
f(x)e-ihn(1+x+b2(x-x))dx. | |
|
(10) |
Интегрируя последние
интегралы по частям, получим желаемый результат.
Нам понадобится также следующая
Лемма 2 [13]. Пусть {a
s } , s = 1, ..., q, 1
Ј q < Ґ , - некоторое
конечное множество комплексных чисел и U Н {as } -
подмножество целых чисел (возможно, пустое). Тогда справедлива формула
|
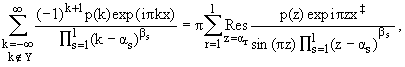
|
где {bs},(s = 1, ..., q) - множество положительных
целых чисел, p(z) - многочлен степени не выше
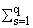 bs-1 и принято
обозначение x‡
= (x + 1) (mod 2) - 1, -1 < x‡ < 1.
bs-1 и принято
обозначение x‡
= (x + 1) (mod 2) - 1, -1 < x‡ < 1.
3. Приведем краткое описание аналога КЕГ-метода (ниже, в
применении к системе (3), его будем называть A-методом) в случае, когда f О Cq+1 на каждом из отрезков [-1,x],[x,1]. Используя леммы 1 и 2, можно представить функцию f в
виде (h = [(2p)/(1+x+b2(1-x))])
| f(x) = P(x) + Q(x) + F(x), | |
(11) |
где
| P(x) = |
q
е
k=0
|
|
hAk
2(ih)k+1
|
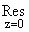 |
eipz ([(h)/(p)]u(x)+1)‡
sin(pz)zk+1
|
, | |
(12) |
| Q(x) = |
q
е
k=0
|
|
hBk
2(ih)k+1
|
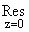 |
eipz ([(h)/(p)](u(x)-x-1)+1)‡
sin(pz)zk+1
|
, | |
(13) |
| u(x) = 1 + xe(x,x) + |
b2 + 1
b2 - 1
|
x(e(x,x) - 1). | |
(14) |
Очевидно (см. (8)),
коэффициенты Фурье {Fn} функции F(x) имеют порядок убывания, равный,
по меньшей мере, o(N-q-1), N ® Ґ. Отсюда следует, что аппроксимационная формула
| SN,q(x) = P(x) + Q(x) + |
N
е
n=-N
|
Fnfn(x) | |
(15) |
сходится (в равномерной метрике) к
f со скоростью порядка o(Nq), N ® Ґ.
4. Переходя к описанию аналога метода QP (ниже будем его называть
B-методом), рассмотрим конечные последовательности комплексных чисел
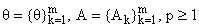 и обозначим
Если k < 0, то примем
и обозначим
Если k < 0, то примем
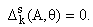
Лемма 3. Пусть f О Cq+1
на каждом из
отрезков [-1,x], [x,1] и m О N, m < q.
Тогда
fn = 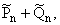 где
где
|
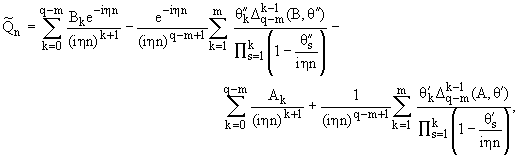 |
(17) |
|
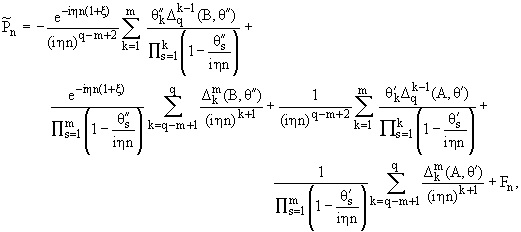 |
(18) |
| Fn = |
1
(ihn)(q+1)
|
|
|
у
х |
1
-1
|
|
f q+1(x)
e(x,x)(q+1)
|
yn(x)dx.
| |
(19) |
Доказательство. Нетрудно
проверить следующее тождество (x № -q1-1):
|
q
е
k=q-m+1
|
Akxk = x
q+1q1 |
Aq - Aq-mx-m
1 + q1x
|
+ |
1
1 + q1x
|
|
|
q
е
k=q-m+1
|
(Ak + q1Ak-1)xk. | |
(20) |
После m-кратного применения того же преобразования
придем к формуле
|
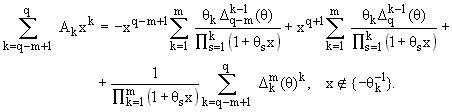 |
(21) |
Доказательство
завершается, если главную часть формулы (7) разделим на четыре суммы
и применим преобразование (21) к первым двум
слагаемым, с заменой x на (ihn)-1.
Из лемм 2 и 3 следует,
что функцию f можно представить в виде
где
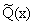 - квазиполином, т.е. конечная линейная комбинация функций вида b(x)ec x,
где b(x) многочлен, c =
- квазиполином, т.е. конечная линейная комбинация функций вида b(x)ec x,
где b(x) многочлен, c = (const) | О C. Если же векторы qў и qўў определить из систем
то P(x) станет q раз непрерывно
дифференцируемой на действительной оси и 2-периодической функцией. В этом случае
аппроксимационная формула
|
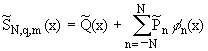 |
(24) |
сходится к f со скоростью порядка
o(N-q), N ® Ґ. По сути, мы применили к асимптотическим степенным (по
z = (ihn)-1) рядам
(7) аппроксимации Паде порядка [(q - m)/m] (см. [14]).
5. В случaе, когда b = 1, наш ряд превращается в обыкновенный ряд
Фурье, а кусочно-квазиполиномиальные функции P(x) и Q(x) становятся обобщенными
полиномами Бернулли. Таким образом, метод A является обобщением КЕГ-метода и,
соответственно, метод B - обобщением QP-метода.
Для того чтобы
изучаемый ряд функции f сходился "хорошо", достаточно потребовать, чтобы функция
f, продолженная на всю действительную ось 2-периодически, была достаточно
гладкой (кроме точек 2n - 1 и x + 2n, где n О Z) и чтобы в точках
x = 2n - 1 и x = x + 2n, n О Z, выполнялись равенства
[(f (k)(x+0))/(b2k)] = f (k)(x - 0), k = 0, 1, ..., q.
6. Численные эксперименты проведены на компьютере с процессором Pentium 4,
512MB RAM, с применением компьютерной системы MATHEMATICA [15]. Для иллюстрации
свойств методов A и B рассмотрим следующую функцию:
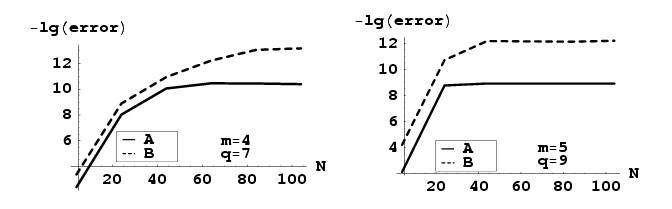
Десятичные логарифмы обратных величин
равномерных
ошибок при аппроксимации функции (25) (b = 2, x
= [ 1/3]).
На рисунке указаны
порядки равномерных ошибок при аппроксимации функции (25) методами A и B для
различных значений N. Левый рисунок соответствует случаю q = 5, m = 3, правый -
случаю q = 7, m = 4.
На этих примерах
хорошо просматривается явное преимущество B-метода как в смысле точности, так и
в смысле устойчивости к накоплению ошибок.
Эти и другие
результаты хорошо согласуются с результатами работы [13] и могут служить
основанием для рекомендации алгоритма B к практическому применению. Приближенные
скачки Ak, Bk могут быть вычислены по коэффициентам
{fn}, |n|
£
N < Ґ аналогично работе [13].
Институт математики НАН РА
Литература
1. Крылов А. О приближенных вычислениях. Лекции,
читанные в 1906 г. СПб. Типилитогр. К. Биркенфельда. 1907. 228
с.
2. Lanczos C. - J. Soc. Indust. Appl. Math., Ser. B Numer. Anal. 1964. V. 1.
P. 76-85.
3. Lanczos C.
Discourse of Fourier Series. Hafner. N.-Y.
1966.
4. Min M.S., Gottlieb
D. - SIAM J. Numer. Anal. 2003. V. 40. N. 6. P.
2254-2269
5. Jones W.B.,
Hardy G. - Math. Comp. 1970. V. 24. P.
47-60.
6. Lyness J.N.
- Math. Comp. 1974. V. 28. P.
81-123.
7. Tasche
M. - Math. Nachr. 1979. V. 90. P.
123-134.
8. Baszenski G.,
Delvos F.J., Tasche M. - Computers and Mathematics with
Applications 1995. V. 30. N 3-6. P
33-49.
9. Gottlieb D., Shu
C.W. - Math. Comp. 1992. V. 43. P.
81-92.
10. Eckhoff K.S.
- Math. Comp. 1995. V. 64. N 210. P. 671 -
690.
11. Eckhoff K.S.,
Wasberg C.E. - Report no. 99. Dept. of Math. University of
Bergen. 1995. P. 1-38.
12. Gelb A., Gottlieb D. - Computers Math. Applic. 1997.
V. 33. N 11. P. 35-58.
13. Нерсесян А.Б. - ДНАН Армении. 2004. Т. 104. N. 4. С.
186-191.
14. Бейкер Дж.,
Грейвс-Моррис П. Аппроксимации Паде. М. Мир. 1986.
502 с.
15. Wolfram
S. The MATHEMATICA book. Fourth Edition. Wolfram
Media. Cambridge University Press. 1999. 1468 p.
|