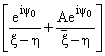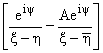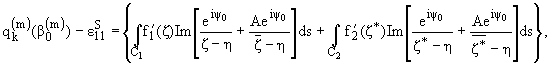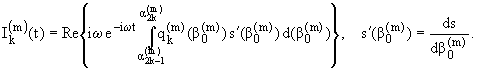б)
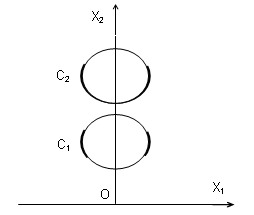
полупространство свободно от сил и граничит с вакуумом
Таким образом, поставленная задача сводится к определению функций
U3 и F* из дифференциальных уравнений (5), граничных
условий (4), (6) или (7).
Следуя [5],
представим искомые функции в виде
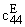 U3(z) = U3(z) = |
у
х
C1
|
p1(z){H0(1)(gr) - AH0(1)(gr1)}ds + |
у
х
C2
|
p2(z*){H0(1)(gr*) - AH0(1)(gr1*)}ds; | |
| F*(z) = |
у
х
C1
|
f1(z) |
¶
¶nz
|
(ln r - A ln r1)ds + |
у
х
C2
|
f2(z*) |
¶
¶nz
|
(ln r* - A ln r1*)ds; | |
(8) |
r = |z - z|, r* = |z* - z|, r1 = |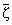 - z|, r1*
= | - z|, r1*
= |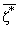 - z| z О C1, z* О
C2, - z| z О C1, z* О
C2, |
|
где
Hn(1)(x) - функция Ханкеля
первого рода порядка n.
Интегральные представления (8) удовлетворяют уравнениям (5) и условиям
излучения на бесконечности. Подставляя предельные значения функций (8) при
z ® z0 О C1 и z ® z0* О
C2 в граничные условия (4), приходим к системе сингулярных
интегродифференциальных уравнений второго рода:
| 2ip1(z0) + |
у
х
C1
|
{p1(z)g1(z, z0) + f ў1(z)g2(z, z0)}ds + | |
| + |
у
х
C2
|
{p2(z*)g1(z*, z0) + f ў2(z*)g2(z*, z0)}ds = 0, z0 О
C1; | |
| 2ip2(z0*) + |
у
х
C1
|
{p1(z)g1(z, z0*) + f ў1(z)g2(z, z0*)}ds + | |
(9) |
| + |
у
х
C2
|
{p2(z*)g1(z*, z0*) + f ў2(z*)g2(z*, z0*)}ds = 0, z0* О
C2; | |
| -pf1(z0) + |
у
х
C1
|
{p1(z)g3(z, z0) + f1(z)g4(z, z0)}ds + | |
| + |
у
х
C2
|
{p2(z*)g3(z*, z0) + f2(z*)g4(z*, z0)}ds = F1*(z0), z0 О
C1f; | |
| -pf2(z0*) + |
у
х
C1
|
{p1(z)g3(z, z0*) + f1(z)g4(z, z0*)}ds + | |
| + |
у
х
C2
|
{p2(z*)g3(z*, z0*) + f2(z*)g4(z*, z0*)}ds = F2*(z0*), z0* О C2f; | |
|
у
х
C1
|
f ў1(z)g5(z, z0)ds + |
у
х
C2
|
f ў2(z*)g5(z*, z0)ds = 0, z0 О
C1\C1F; | |
|
у
х
C1
|
f ў1(z)g5(z, z0*)ds + |
у
х
C2
|
fў2(z*)g5(z*, z0*)ds = 0, z0 О
C2\C2F; | |
| g1(x, h) = |
2
pi
|
Re |
eiy0
x - h
|
+ g[H1(gr0)cos(y0 - a0) - AH1(1)(gr10)cos(y0 - a10)]; | |
g2(x, h) =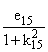 g5(x, h), g3(x, h) = g5(x, h), g3(x, h) =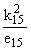 [H0(1)(gr0) - AH0(1)(gr10)]; [H0(1)(gr0) - AH0(1)(gr10)]; |
|
g5(x, h)Im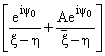 , H1(x) = , H1(x) = |
2i
px
|
+ H1(1)(x); | |
g4(x, h) = Re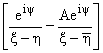 , r0 = |x - h|, r10 = | , r0 = |x - h|, r10 = |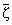 - h| f ўm(z) = - h| f ўm(z) = |
dfm
ds
|
; | |
a0 = arg(x - h), a10 = arg(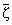 - h), y0 = y(h), y = y(x). - h), y0 = y(h), y = y(x). |
|
Здесь y - угол между нормалью к контуру C и
осью x1, Fm*(h) - кусочно-постоянные функции, задающие значения
электрического потенциала на электродах. Определив функции pm(z) и fm(z) из системы
(9), по формулам (3) с использованием представлений (8) можно определить все
полевые величины в полупространстве с двумя
отверстиями.
Найдем выражение для амплитуды
плотности распределения электрических зарядов qk(m)(b(m)) на k-м электроде, расположенном на контуре
Cm (m = 1,2). Вводя параметризацию контуров с помощью равенств z = z(b(1)), z* = z*(b(2)) (0 Ј b(m) Ј 2p) и учитывая то, что отверстия сопряжены с вакуумом, запишем
qk(m)(b(m)) = Dn(m,k)(b(m)), 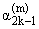 (m) < b(m) < (m) < b(m) < 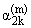 (m = 1,2). (m = 1,2). | |
(10) |
Здесь Dn(m,k)(b(m)) представляет собой амплитуду нормальной
компоненты вектора электрической индукции на соответствующем электродированном
участке контура Cm.
Используя
представление (8) для функции F*(x1,x2), с
учетом (4) и (10) находим
|
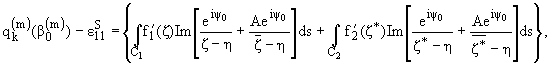 |
(11) |
где h(b0(m)) О Cmfk,
Cmfk - часть контура
Cm, на которой расположен k-й электрод.
Интегрируя выражение (11) в пределах от
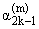 до
до
 , получим амплитудное
значение суммарного заряда Qk(m) k-го электрода на контуре
Cm, отнесенное к единице его длины. Ток, протекающий через данный
электрод, можно определить по формуле
, получим амплитудное
значение суммарного заряда Qk(m) k-го электрода на контуре
Cm, отнесенное к единице его длины. Ток, протекающий через данный
электрод, можно определить по формуле
|
 |
(12) |
В
качестве примера рассмотрим полупространство (керамика PZT-4 [6]) с двумя
круговыми отверстиями, описываемыми уравнениями
| z = Reib(1) + a, z* = Reib(2) + b, b(m) О
[0,2p]. | |
(13) |
Возбуждение электроупругих полей осуществляется четырьмя электродами,
попарно расположенными на поверхности каждой полости (a1(m) = -p/7, a2(m) = p/7,
a3(m ) = 6p/7, a4(m) = 8p/7,
m = 1,2). В расчетах полагали a / R = 3, b / R = 7.
Решение системы интегродифференциальных уравнений (9) с учетом (13)
проводилось численно по специальной схеме метода квадратур [1].
|
|
На рис. 2 показано изменение величин
Qm*=|Q1(m)/( F*)| (m = 1,2) в функции
нормализованного волнового числа gR в случае свободного
полупространства (A=-1). Кривые 1, 3 и 2, 4 построены
для случаев нагружения F1(1) = F1(2) = F*, F2(1) = F2(2) = -F* и F1(1) = -F1(2) = F*, F2(1) = -F2(2) = -F* соответственно. Линии 1 и 2 относятся к
величине Q1*, линии 3 и 4 - к величине
Q2*. Аналогичные результаты в случае закрепленного
полупространства (A = 1) для тех же значений параметров и в том же соответствии
показаны на рис. 3.
F*)| (m = 1,2) в функции
нормализованного волнового числа gR в случае свободного
полупространства (A=-1). Кривые 1, 3 и 2, 4 построены
для случаев нагружения F1(1) = F1(2) = F*, F2(1) = F2(2) = -F* и F1(1) = -F1(2) = F*, F2(1) = -F2(2) = -F* соответственно. Линии 1 и 2 относятся к
величине Q1*, линии 3 и 4 - к величине
Q2*. Аналогичные результаты в случае закрепленного
полупространства (A = 1) для тех же значений параметров и в том же соответствии
показаны на рис. 3.
Из анализа результатов
следует, что влияние динамического эффекта на поведение компонентов
электроупругого поля в полупространстве с отверстиями проявляется более
существенно, чем в пространстве [2]. Как видно из рис. 3 (кривая 2), вследствие
динамического эффекта величина Q1* может превысить свой
статический аналог на 57% . Расчет показывает, что распределение перемещения и
напряжений в области кусочно-однородного полупространства в значительной мере
зависит от частоты гармонического нагружения и значений задаваемых на системе
электродов электрических потенциалов.
Рассмотренный подход к исследованию электроупругого поля в
полупространстве с отверстиями может быть применен для расчета характеристик
перфорированных пьезоэлектрических преобразователей различной геометрии при
электрическом нагружении с помощью многоэлектродных систем.
Работа выполнена в рамках договора о научном
сотрудничестве между Институтом механики НАН РА и Афинским национальным
техническим университетом.
Афинский национальный технический
университет, Греция
Сумский государственный
университет, Украина