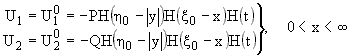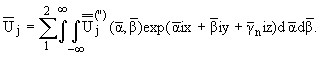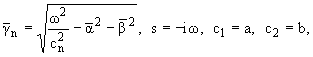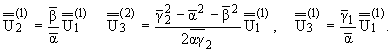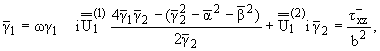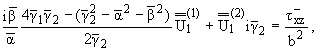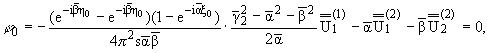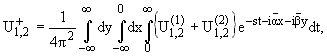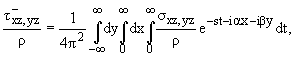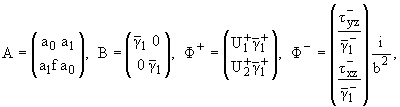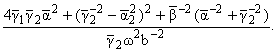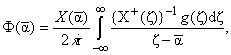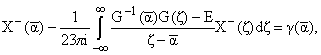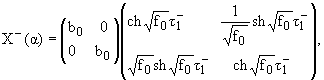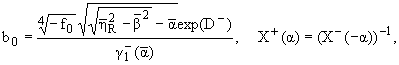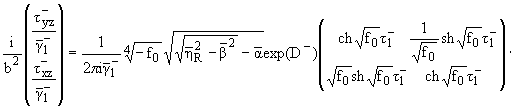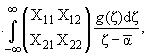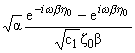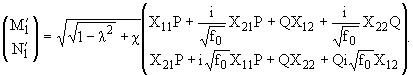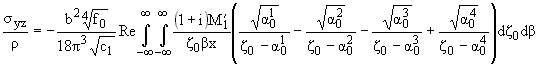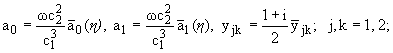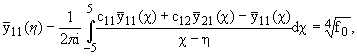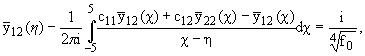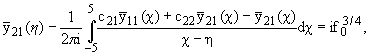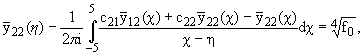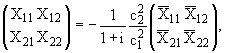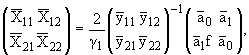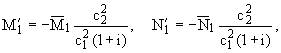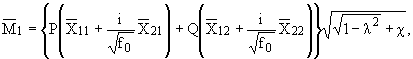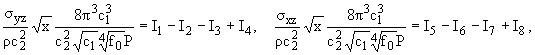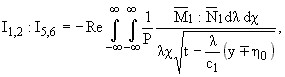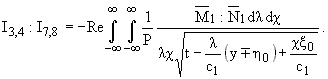МЕХАНИКА
УДК 539.1
Член корреспондент НАН РА А. Г. Багдоев, А. Н.
Мартиросян,
С. М. Погосян
Решение cмешанной динамической граничной задачи для
упругого
полупространства
(Представлено 30/III 2005)
Рассматривается задача о движении изотропного
упругого полупространства z і 0, на границе которого
вдоль полуплоскости x і 0 заданы горизонтальные
перемещения, а вдоль x і 0 граница свободнa от
напряжений. Решение получено методом интегральных преобразований Лапласа по
времени t и преобразований Фурье по координатам x,y и приводится к системе
Винера - Хопфа, которая решается методами сингулярных интегральных уравнений и
циркулянтов. Вычисляются коэффициенты интенсивности касательных напряжений около
края полуплоскости z = 0, x = 0, |y| < Ґ. Метод циркулянтов при
решении системы уравнений Винера - Хопфа предложен в [1].
Аналогичная данной статическая задача
методом Винера - Хопфа решена в [2]. Приведение задачи Гильберта к системе
Фредгольма дано в книге [3]. В настоящей работе дается численное решение
вышеуказанной системы Фредгольма и вычисление интегралов для коэффициентов
интенсивности касательных напряжений.
1. Сведение задачи к системе Винера - Хопфа. Выберем оси
координат x,y в плоскости поверхности, ось z по нормали к указанной плоскости;
ось y направлена вдоль прямой раздела граничных условий. Пусть
Uj, J = 1, 2, 3, есть компоненты перемещений вдоль осей x, y, z. Уравнения
движения упругой среды имеют вид
| x1 = x, x2 = y, x3 = z, (a2 - b2) |
¶
¶xj
|
|
¶Uk
¶xk
|
+ b2DUj = |
¶2U
¶t2
|
, | |
(1.1) |
где a, b - скорости упругих волн,
D - оператор Лапласа.
Граничные
условия берутся в форме (z = 0, |y| < Ґ)
| szz = 0,
-Ґ
< x < Ґ; sxz=0, syz=0, -Ґ < x <
0, | |
(1.2) |
где P, Q, h0, x0 -
постоянные, H(x) - единичная функция.
Обозначив через
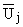 преобразования Лапласа по t от Uj, через
преобразования Лапласа по t от Uj, через
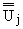 -
преобразования Фурье по x, y от
-
преобразования Фурье по x, y от
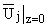 можно записать
можно записать
|
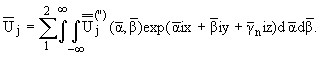 |
(1.4) |
Подставляя (1.4) в (1.1), получим
где
s - параметр преобразования Лапласа.
Кроме
того из (1.1) имеет место
|
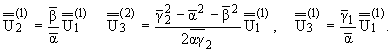 |
(1.5) |
Подставив (1.4) в граничные условия (1.2), (1.3) и обращая
преобразования Фурье по x,y, получим
|
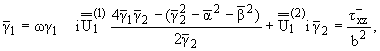 |
(1.6) |
где
индекс (+) дает функции, аналитические в верхней полуплоскости
 , а индекс (-) дает
аналитические функции в нижней полуплоскости
, а индекс (-) дает
аналитические функции в нижней полуплоскости
 .
.
Исключая из (1.6)
функции
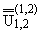 , можно получить систему
Винера - Хопфа
, можно получить систему
Винера - Хопфа
где
C = A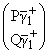 j0, j0, |
|
(1.9) |
a0 =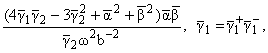
|
|
a1 =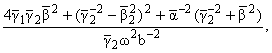
|
|
a1f =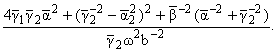
|
|
(1.10) |
Система уравнений (1.8) имеет обычный вид
[1], здеcь введен циркулянт A, что позволяет для настоящей задачи найти
асимптотику решения для
 ® Ґ в
замкнутом виде.
® Ґ в
замкнутом виде.
2. Решение
задачи Гильберта для произвольного
 . Уравнение (1.8) может быть записано в виде задачи
Гильберта
. Уравнение (1.8) может быть записано в виде задачи
Гильберта
где
G( )= -A-1B = )= -A-1B = |
ж
з
з
з
з
з
и
|
|
|
ц
ч
ч
ч
ч
ч
ш
|
, g = |
ж
з
и |
-Pg1+
-Qg1+
|
ц
ч
ш |
, | |
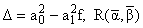 - функция Рэлея.
- функция Рэлея.
Решение задачи (2.1), ограниченное на
бесконечности, дано в [3] в виде
|
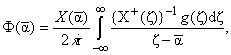
|
(2.2) |
где матрицы функции x( ) удовлетворяют однородным
уравнениям
) удовлетворяют однородным
уравнениям
X+( ) = G( ) = G( )X-( )X-( ), G( ), G( ) = X+( ) = X+( ){X-( ){X-( )}-1. )}-1. |
|
(2.3) |
Как показано в [3], уравнение для x( ) в (2.3) можно привести к системе интегральных уравнений
Фредгольма
) в (2.3) можно привести к системе интегральных уравнений
Фредгольма
|
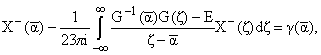
|
(2.4) |
где g есть асимптотическое поведение X-(
есть асимптотическое поведение X-( ) для
) для
 »
Ґ. Здесь интеграл берется в смысле главного значения
Коши, X-(
»
Ґ. Здесь интеграл берется в смысле главного значения
Коши, X-( ) после факторизации G(
) после факторизации G( ) дается следующей асимптотической формулой:
) дается следующей асимптотической формулой:
|
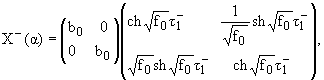 |
(2.5) |
где
hR = [(w)/(cR)]
есть корень уравнения Рэлея для плоской задачи. Здесь все факторизуемые функции
удовлетворяют условиями теоремы B из [5].
Из
(2.2) с учетом (1.9), (2.5), вводя обозначения
X+( ) = ) = |
ж
и |
X11 X12
X21 X22
|
ц
ш |
-1
|
, X-( ) = ) = |
ж
и |
y11 y12
y21 y22
|
ц
ш |
| |
(2.6) |
для больших
 , соответствующих малым x,
можно получить
, соответствующих малым x,
можно получить
|
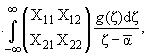 |
(2.7) |
где XjK даются (2.3),
(2.5) заменой
 на z.
на z.
Соотношения (2.7) для
касательных напряжений вблизи края z = 0, x » 0, x >
0, после обратных интегральных преобразований, дают асимптотику, где в
коэффициенте перед интегралом в (2.7) взято
 » Ґ, в
форме
» Ґ, в
форме
|
syz
b2r
|
= |
1
16p3
|
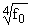 |
ж
з
и |
|
1 + i
2pi
|
|
ц
ч
ш |
|
s+iҐ
у
х
s-iҐ
|
ds |
Ґ
у
х
-Ґ
|
db |
Ґ
у
х
-Ґ
|
da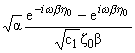 |
· | |
| · |
Ґ
у
х
-Ґ
|
Mў1(1 - eiwz0x0)es(t-ax-by) |
dz0
z0 - a
|
, | |
(2.8) |
где
 = wa,
= wa,
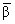 = wb, b =
[1/(c1)]l, z =
z0w, z0 = [1/(c1)]c,
= wb, b =
[1/(c1)]l, z =
z0w, z0 = [1/(c1)]c,
|
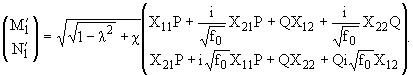 |
(2.9) |
Обозначая f1,2 = t - ax - by ± bh0, f3,4 = t - ax - by ± bh0 + z0x0, вычисляя интеграл в (2.8) по s и после этого
интеграл от дельта-функции по a d(f1,2) d(f3,4), можно получить решение в форме Смирнова -
Соболева.
Пусть
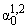 и
и
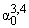 есть корни уравнений
f1,2 = 0, f3,4 = 0,
есть корни уравнений
f1,2 = 0, f3,4 = 0,
|
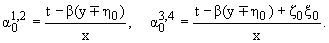 |
(2.10) |
Для x » 0 из (2.8), (2.10) можно получить
|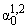 | » Ґ, | | » Ґ, |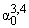 | » Ґ, | » Ґ, | |
|
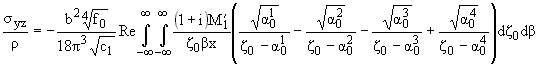 |
(2.11) |
и такое же выражение для [(syz)/(r)] заменой
M1ў на N1ў.
Поскольку для больших
a X-(a) = g(a) и
из (2.5)
|
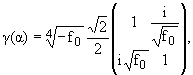 |
(2.12) |
из (2.4), (2.6) можно получить
систему интегральных уравнений Фредгольма
|
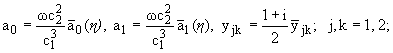 |
(2.13) |
|
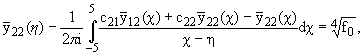 |
(2.14) |
где вместо (-Ґ,Ґ) взят
для вычислений интервал интегрирования (-5,5), что возможно для приближенных
расчетов сходящихся интегралов.
В силу (2.4),
(2.1) в (2.14)
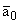 (h),
(h),
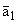 (h), f(h) даны в (1.10), (2.13).
(h), f(h) даны в (1.10), (2.13).
3. Численный расчет коэффициентов интенсивности
напряжений. При расчете решений системы (2.14) интегралы заменяются
суммами и решение ищется в точках l,h = 0, 1, 2, 3, 4, 5, -1, -2, -3, -4, -5.
После определeния
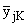 из (2.3),
(2.6) можно получить
из (2.3),
(2.6) можно получить
|
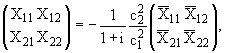 |
(3.1) |
|
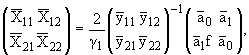
|
(3.2) |
функции в (3.2) зависят от
аргументов c, l,
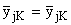 (c) По формулам
(2.9), (2.11) с учетом (2.13), обозначая
(c) По формулам
(2.9), (2.11) с учетом (2.13), обозначая
|
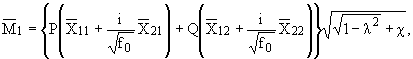 |
(3.3) |
получим
напряжения вблизи оси y для x > 0 в виде (Q = 0)
|
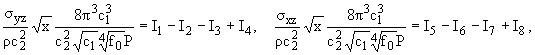 |
(3.4) |
где
|
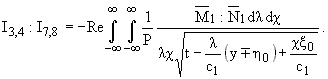 |
(3.5) |
Интегралы в (3.5) взяты в смысле главной части Коши. В (3.4), (3.5)
считается, что t = 0,1;1;3 [(x0)/(c1t)] = 1, [(h0)/(c1t)] = 1, y = 0. Значения x0,h0 различны
для трех величин t.
Результаты расчетов
I1 - I2 - I3 + I4, I5 - I6 - I7 + I8 приведены в таблице.
| t |
0.1 |
1 |
3 |
| I1 - I2 - I3 + I4 |
-0.02 × 105 |
-0.0066 × 105 |
-0.0.38 × 105 |
| I5 - I6 - I7 + I8 |
0.076 × 105 |
0.024 × 105 |
0.013 × 105 |
Так как в левых частях (3.4) коэффициент при
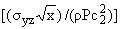 и
и
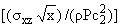 имеет порядок 105,
для
имеет порядок 105,
для
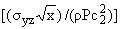 и
и
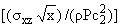 получится соответственно -0.02, -0.0066, -0.0038 и 0.076, 0.024, 0.013.
получится соответственно -0.02, -0.0066, -0.0038 и 0.076, 0.024, 0.013.
Гориcский филиал Государственного инженерного
университета Армении
Институт меxаники НАН
РА
Литература
1. Саркисян В. С. Караханян И. М. B cб: Проблемы механики тонких деформируемых тел. K 80-летию академика
НАН PА С. А. Амбарцумяна. Ереван. 2002. C. 266-280.
2. Петросян С. З. Об одном классе смешанных задач для
неоднородного по степенному закону упругого полупространства. Канд. дис. Ин-т
механики НАН PА. Ереван. 2002.
3. Векуа Н.
П. Системы сингулярных интегральных уравнений. М. 1970. 379 с.
4. Мартиросян А. Н. Краевые
задачи нестационарного движения анизотропных и изотропных упругих сред. Докт.
дис. Ин-т механики НАН PА. Ереван 1990. 272 с.
5. Нобл Б. Метод Винера - Хопфа. М. ИЛ. 1962. 278 с.
![]() преобразования Лапласа по t от Uj, через
преобразования Лапласа по t от Uj, через
![]() -
преобразования Фурье по x, y от
-
преобразования Фурье по x, y от
![]() можно записать
можно записать ![]() , а индекс (-) дает
аналитические функции в нижней полуплоскости
, а индекс (-) дает
аналитические функции в нижней полуплоскости
![]() .
.![]() , можно получить систему
Винера - Хопфа
, можно получить систему
Винера - Хопфа ![]() ® Ґ в
замкнутом виде.
® Ґ в
замкнутом виде.![]() . Уравнение (1.8) может быть записано в виде задачи
Гильберта
. Уравнение (1.8) может быть записано в виде задачи
Гильберта ![]() есть асимптотическое поведение X-(
есть асимптотическое поведение X-(![]() ) для
) для
![]() »
Ґ. Здесь интеграл берется в смысле главного значения
Коши, X-(
»
Ґ. Здесь интеграл берется в смысле главного значения
Коши, X-(![]() ) после факторизации G(
) после факторизации G(![]() ) дается следующей асимптотической формулой:
) дается следующей асимптотической формулой: ![]() на z.
на z.![]() » Ґ, в
форме
» Ґ, в
форме ![]() и
и
![]() есть корни уравнений
f1,2 = 0, f3,4 = 0,
есть корни уравнений
f1,2 = 0, f3,4 = 0, ![]() (h),
(h),
![]() (h), f(h) даны в (1.10), (2.13).
(h), f(h) даны в (1.10), (2.13).![]() из (2.3),
(2.6) можно получить
из (2.3),
(2.6) можно получить