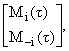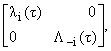СИСТЕМЫ УПРАВЛЕНИЙ
УДК 62-501.7
С. О. Симонян, Ф. П. Григорян
Синтез одномерного управления с наперед заданным спектром
в
нестационарной интегро-дифференциальной системе уравнений
(Представлено академиком А. А. Терзяном 26/I 2005)
Постановка задачи. Пусть
задана равномерно в [t0,t1] управляемая система
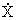 (t) = A(t)X(t) + B(t)u(t), (t) = A(t)X(t) + B(t)u(t), | |
| u(t) = |
t
у
х
-Ґ
|
g(t - tў,tў)n(tў)dtў, | |
или
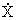 (t) = A(t)X(t) + B(t) (t) = A(t)X(t) + B(t) |
t
у
х
-Ґ
|
g(t - tў,tў)b(tў)X(tў)dtў, | |
(1) |
где
X(t) = (x1(t),x2(t),...,xn(t))T -
(n×1) - мерный вектор переменных состояния; n(t) -
скалярный входной сигнал регулятора; g(t - tў,tў) - скалярная импульсная
переходная функция регулятора; u(t) - скалярное управляющее воздействие
(выходной сигнал регулятора).
Пусть
A(t) = (aij(t)), i,j =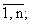 B(t) = (h1(t),h2(t),...,hn(t))T;
b(t) = (b1(t),b2(t),...,bn(t)) и A(t), B(t),
b(tў), g(t - tў,tў) дифференцируемы по своим
аргументам любое необходимое число раз. Требуется построить b(tў) так, чтобы решение системы (1) имело вид
B(t) = (h1(t),h2(t),...,hn(t))T;
b(t) = (b1(t),b2(t),...,bn(t)) и A(t), B(t),
b(tў), g(t - tў,tў) дифференцируемы по своим
аргументам любое необходимое число раз. Требуется построить b(tў) так, чтобы решение системы (1) имело вид
| X(t) = K(t)Y(t) = |
n
е
i=1
|
ki(t)yi(t), | |
(2) |
где
Y(t) = (y1(t),y2(t),...,yn(t))T -
решение системы
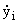 (t) = li(t)yi(t),
i = (t) = li(t)yi(t),
i =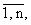 |
|
(3) |
причем
K(t) = [k1(t),k2(t),...,kn(t)] - некоторая
невырожденная матрица порядка n с векторами-столбцами ki(t), i =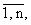 подлежащая определению; li(t), i =
подлежащая определению; li(t), i =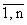 - наперед
заданные, необходимое число раз дифференцируемые на
[t0,t1] функции, удовлетворяющие
условиям:
- наперед
заданные, необходимое число раз дифференцируемые на
[t0,t1] функции, удовлетворяющие
условиям:
1. |li(t) - lj(t)| >
0, i № j, i,j =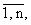
2. li(t), i =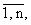 не
совпадают с нулями и особыми точками передаточной функции
регулятора,
не
совпадают с нулями и особыми точками передаточной функции
регулятора,
3. li(t), i =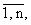 не
пересекаются хотя бы с одним из собственных значений матрицы A(t), т.е. |ci(t) - lj(t)| > 0, i № j, i,j =
не
пересекаются хотя бы с одним из собственных значений матрицы A(t), т.е. |ci(t) - lj(t)| > 0, i № j, i,j =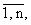 где ci(t),
i =
где ci(t),
i =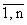 - собственные значения матрицы
A(t).
- собственные значения матрицы
A(t).
Решение задачи.
Пусть матрица управляемости S(t) имеет ранг n в любой точке t заданного
интервала [t0,t1], т.е. [1-4]
| rang S(t) = rang(S1(t),
S2(t),...,Sn(t)) = n, | |
где
Sk(t) = A(t)Sk-1(t) -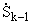 (t), k = (t), k =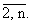 |
|
Выполнив в системе (1) преобразование [5]
получим [3]
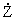 (t) = A0(t)Z(t) + B0 · (t) = A0(t)Z(t) + B0 · |
t
у
х
-Ґ
|
g(t - tў,tў)q(tў)Z(tў)dtў, | |
(5) |
где
| q(tў) = b(tў)S(tў) = (q1(tў),q2(tў),...,qn(tў)), | |
а
структуры A0(t) и B0 можно найти в
[3,4].
Полагая, что элементы матриц A(t) и
q(tў), а также g(t - tў,tў) как функция от аргумента
tў являются медленно меняющимися функциями [1], введем
так называемое медленное время t = et, и вместо уравнения (5) рассмотрим уравнение более общего
вида
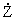 (t,e) = A0(t)Z(t,e) + B0 (t,e) = A0(t)Z(t,e) + B0 |
t
у
х
-Ґ
|
g(t - tў,rў)q(rў,e)Z(tў,e)dtў, | |
(6) |
(очевидно, что при e = 1 система (6) совпадает с системой (5)).
Для решения задачи воспользуемся методом
матричныx и асимптотических разложений по малому параметру. При этом заметим,
что расcматриваемая система равномерно управляема на интервале
[t0,t1], ввиду чего свойство управляемости системы
остается инвариантным относительно используемых
преобразований.
Сделаем в системе (6) замену
переменных по аналогии с (2):
| Z(t,e) = K(t,e)Y(t,e) = |
n
е
i=1
|
ki(t,e)yi(t,e), | |
(7) |
где K(t,e) = (k1(t,e),k2(t,e),...,kn(t,e)) - некоторая невырожденная
матрица порядка n с векторами-столбцами ki(t,e), i =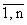 подлежащая определению, причем по аналогии с (3)
подлежащая определению, причем по аналогии с (3)
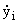 (t,e) = li(t)yi(t,e), i = (t,e) = li(t)yi(t,e), i =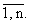 |
|
(8) |
Очевидно, что
| yi(t,e) = ciexp |
t
у
х
t0
|
li(tў)dtў, i =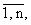 |
|
(9) |
где ci - произвольные
постоянные. С учетом (6) и (7) имеем
|
n
е
i=1
|
|
й
к
л |
e |
dki(t,e)
dt
|
+ ki(t,e)li(t) |
щ
ъ
ы |
yi(t,e)
= | |
| = |
n
е
i=1
|
|
й
к
л |
A0(t)ki(t,e)yi(t,e) + B0 |
t
у
х
-Ґ
|
g(t - tў,tў)q(tў,e)ki(tў,e)yi(tў,e)dtў |
щ
ъ
ы |
. | |
Выбор ki(tў,e) и qi(tў,e)
ограничим требованием выполнения равенств [1]
|
й
к
л |
e |
dki(t)
dt
|
+ ki(t,e)li(t) |
щ
ъ
ы |
yi(t,e)
= | |
| = A0(t)ki(t,e)yi(t,e) + B0 |
t
у
х
-Ґ
|
g(t - tў,rў)q(tў,e)ki(tў,e)yi(tў,e)dtў, i =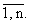 |
|
(10) |
Из
(8)-(10) следует, что
| e |
dki(t,e)
dt
|
+ ki(t,e)li(t) = A0(t)ki(t,e) + | |
| + B0 |
t
у
х
-Ґ
|
|
й
к
л |
g(t - tў,rў)q(tў,e)ki(tў,e)exp |
ж
з
и |
|
tў
у
х
t0
|
li(t,e)dt - |
t
у
х
t0
|
li(tў,e)dtў |
ц
ч
ш |
|
щ
ъ
ы |
, i =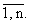 |
|
(11) |
В
интеграле правой части (11) сделаем замену переменной t - tў = s, откуда tў = t - s и dtў = -ds, следовательно из t = et следует tў = etў = e(t - s) = et - es = t - es. Поэтому уравнение (11)
приобретает вид
| e |
dki(t,e)
dt
|
+ ki(t,e)li(t) = A0(t)ki(t,e) + | |
| + B0 |
Ґ
у
х
t0
|
{g(s,t - es)q(t - es,e)ki(t - es,e)exp[qi(t - s,e) - qi(t,e)]}ds, | |
(12) |
где qi(t), i =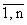 -
функции, удовлетворяющие соотношениям
-
функции, удовлетворяющие соотношениям
|
dqi(t)
dt
|
= li(t),
i =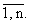 |
|
Следовательно
|
tў
у
х
t0
|
li(t,e)dt - |
t
у
х
t0
|
li(tў,e)dtў = qi(t,e) |
кtў
к
кt0 |
- qi(tў,e) |
кt
к
кt0 |
=
| |
| = qi(tў,e) - qi(t0,e) - qi(t,e) + qi(t0,e) = qi(t - s,e) - qi(t,e). | |
Далее воспользуемся разложениями для ki(t - es,e), q(t - es,e),
exp[qi(t - s,e) - qi(t,e)], q(s,t - es) [1],
а также
| b(t,e) = b[0](t) + eb[1](t) + ... + enb[n](t) + ... = q(t,e)S-1(t) =
| |
| = |
й
к
л |
q[0](t) + |
Ґ
е
k=1
|
ekq[k](t) |
щ
ъ
ы |
S-1(t), | |
(13) |
откуда
| b[k](t) = q[k](t)S-1(t),
k = 0,1,2,... | |
(14) |
Обозначим [1]
| R00(l,t)
є R(l,t) = |
Ґ
у
х
t0
|
g(s,t)exp(-ls)ds, | |
(15) |
| Rsj(l,t) є |
¶s+jR(l,t)
¶ls¶tj
|
= (-1)s |
Ґ
у
х
t0
|
|
¶jg(s,t)
¶tj
|
ssexp(-ls)ds, s,
j = 0,1,2,.... | |
(16) |
R00(l,t) є R(l,t) можно трактовать как передаточную функцию регулятора с
параметрами, "замороженными" в момент времени t (т.е. постоянными величинами,
соответствующими моменту времени t) [1].
Подставим выражения из [1] и (13) в уравнения (12) и приравняем
коэффициенты при одинаковых степенях e,
воспользовавшись соотношениями (15), (16). При этом получим бесконечную систему
уравнений для последовательного определения искомых членов разложений
ki(t,e) и q(t,e).
Покажем, как определяются из этих уравнений искомые величины, имея в
виду, что они содержат члены нулевого, первого, второго, ...
порядка.
Определение членов
нулевого порядка. Приравнивая коэффициенты при нулевой степени e, из (12) получим
| ki[0](t)li(t) = |
й
к
л |
A0(t) + B0 |
Ґ
у
х
t0
|
g(s,r)exp(-li(t)s)dsq[0](t) |
щ
ъ
ы |
ki[0](t). | |
(17) |
Положим
U(i)(t)
є U(li(t),t) = A0(t) + B0R(li(t),t)q[0](t),
i =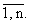 |
|
(18) |
Следовательно, с учетом (15), (16)
и (18) соотношение (17) можно представить в виде
U(i)(t)ki[0](t) = li(t)ki[0](t), i =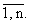 |
|
(19) |
Последние равенства, естественно, имеют место тогда, когда li(t), i =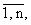 являются собственными значениями матрицы
U[i](t), а ki[0](t), i =
являются собственными значениями матрицы
U[i](t), а ki[0](t), i =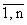 - соответствующими их
собственными векторами.
- соответствующими их
собственными векторами.
Вектор-строку
q[0](t) = (q1[0](t),q2[0](t),...,qn[0](t)) с размерами 1 × n можно вычислить в соответствии с
результатами, полученными в [6]. Имея q[0](t), далее нетрудно построить матрицу собственных векторов
ki[0](t) матрицы U(li(t),t).
По первому условию
задачи и в соответствии с результатами, полученными в [6], легко заключить, что
|
det
|
K[0](t) = (k1[0](t),k2[0](t),...,kn[0](t)) №
0. | |
Обозначим
| M(t) = [K[0](t)]-1 = |
ж
з
з
з
з
и
|
|
ц
ч
ч
ч
ч
ш
|
, | |
(20) |
где Mi(t), i =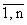 - вектор-строки с
размерами 1 × n. Тогда в соответствии с [1] будем иметь:
- вектор-строки с
размерами 1 × n. Тогда в соответствии с [1] будем иметь:
| U[i](t) · ki[0](t) = li(t) · ki[0](t), | |
| Mi(t) · U[i](t) = li(t) · Mi(t), | |
Mi(t) · ki[0](t) = 1, i =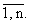 |
|
Пусть
| Pi(t) = ki[0](t) · Mi(t), | |
P-i(t) = En - Pi(t) =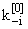 (t) · M-i(t), i = (t) · M-i(t), i =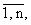 |
|
где
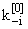 (t) и M-i(t) - матрицы с размерами n × (n - 1) и
(n - 1) × n соответственно. Тогда матрицы
(t) и M-i(t) - матрицы с размерами n × (n - 1) и
(n - 1) × n соответственно. Тогда матрицы
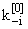 (t) и
M-i(t) друг с
другом и с матрицами ki[0](t) и
Mi(t) связаны соотношениями
(t) и
M-i(t) друг с
другом и с матрицами ki[0](t) и
Mi(t) связаны соотношениями
M-i(t) · 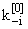 (t) = En-1,
M-i(t) · ki[0](t) = 0, Mi(t) · ki[0](t) = 0. (t) = En-1,
M-i(t) · ki[0](t) = 0, Mi(t) · ki[0](t) = 0. | |
Далее,
если обозначим
k(i)(t) = лki[0](t),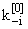 (t)ы,
M(i)(t) = (t)ы,
M(i)(t) =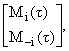 | |
(21) |
L(i)(t) =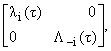 L-i(t) = M-i(t) · U(i)(t) · L-i(t) = M-i(t) · U(i)(t) ·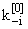 (t), (t), | |
(22) |
то нетрудно убедиться, что
| U(i)(t) = k(i)(t) · L(i)(t) · Mi(t), | |
(23) |
M(i)(t) · k(i)(t) = k(i)(t) · M(i)(t) = En, i =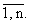 |
|
(24) |
Заметим также, что собственными
значениями матрицы L-i(t) служат собственные
значения lj(i)(r), j =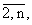 матрицы U(i)(t).
матрицы U(i)(t).
Определение членов первого порядка. Приравнивая коэффициенты при
первой степени e в (12) и имея в виду (15), (16) и
(18), получаем
ki[1](t) · li(t) = U(i)(t) · ki[1](t) + B0 · R00(li(t),t) · q[1](t) · ki(t) - Di[0](t), i =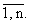 |
|
(25) |
Заметим, что вектор-столбец Di[0](r) будет
известeн при известных ki(t),
q[0](t) и заданных li(t), i =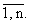
Выражение (25)
напишем в следующем виде:
U(i)(t) · ki[1](t) = ki[1](t) · li(t) - B0 · R00(li(t),t) · q[1](t) · ki(t) + Di[0](t), i =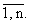 |
|
(26) |
Заменим в (26) U(i)(t) выражением
(23). Тогда получим
| k(i)(t) · L(i)(t) · M(i)(t) · ki[1](t) = ki[1](t) · li(t) - | |
- B0 · R(li(t),t) · q[1](t) · ki(t) + Di[0](t), i =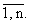 |
|
Умножив теперь последнее равенство слева на M(i)(t), согласно (21) будем иметь
| L(i)(t) · M(i)(t) · ki[1](t) = M(i)(t) · ki[1](t) · li(t) - | |
- M(i)(t) · B0 · R(li(t),t) · q[1](t) · ki(t) + M(i)(t)Di[0](t), i =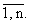 |
|
(27) |
Обозначим
| xi[1](t) = M(i)(t) · ki[1](t) = |
ж
з
и |
Mi(t) · ki[1](t)
M-i(t) · ki[1](t)
|
ц
ч
ш |
= |
ж
з
и |
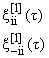
|
ц
ч
ш |
, i =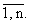 |
|
(28) |
Тогда (27) примет следующий вид:
| L(i)(t) · xi[1](t) = xi[1](t) · li(t) - M(i)(t) · B0 · R(li(t),t) · q[1](t) · ki(t) + | |
+ M(i)(t)Di[0](t), i =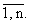 |
|
(29) |
Согласно (21)-(22) и (28) равенство (29) распадается на систему
следующих соотношений:
Mi(t) · B0 · R(li(t),t) · q[1](t) · ki(t) = Mi(t) · Di[0](t), i =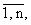 |
|
(30) |
L-i(t) ·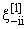 (t) = (t) =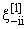 (t) · li(t) - M-i(t) · B0 · R(li(t),t) · q[1](t) · ki(t) + (t) · li(t) - M-i(t) · B0 · R(li(t),t) · q[1](t) · ki(t) + | |
+ M-i(t) · Di[0](t), i =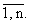 |
|
(31) |
Пусть Mi(t) = (mi1(t),mi2(t),...,min(t)), i =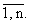 Кроме того предположим, что mi1(t) № 0, i =
Кроме того предположим, что mi1(t) № 0, i =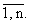 Тогда (30) принимает вид
Тогда (30) принимает вид
| q[1](t) · ki[0](t) = |
Mi(t) · Di[0](t)
mi1(t) · R(li(t),t)
|
, i =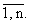 |
|
(32) |
Объединив соотношения (32), получим
| q[1](t) · [k1[0](t),k2[0](t),...,kn[0](t)] = | |
|
й
к
л |
|
M1(t) · D1[0](t)
m11(t) · R(l1(t),t)
|
, |
M2(t) · D2[0](t)
m21(t) · R(l2(t),t)
|
,..., |
Mn(t) · Dn[0](t)
mn1(t) · R(ln(t),t)
|
|
щ
ъ
ы |
= Q[0](·). | |
(33) |
Согласно (20) выражение (33) преобразуется в
| q[1](t) = Q[0](·) · M(t). | |
(34) |
Используя (13), (14), из (34)
найдем
| b[1](t) = Q[0](·) · M(t) · S-1(t). | |
Теперь
вернемся к уравнению (31), которое при (32) принимает следующий вид:
[li(t) · En-1 - L-1(t)] ·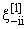 (t) = M-i(t) (t) = M-i(t) |
й
к
л |
|
B0 · Mi(t)
mi1(t)
|
- En |
щ
ъ
ы |
· Di[0](t). | |
(35) |
Матрица L-i(t) не имеет собственных значений, равных li(t). Следовательно,
[li(t)·En-1 - L-i(t)] является невырожденной матрицей, и из равенства (35)
можно определить
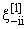 (t):
(t):
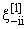 (t) = [li(t) · En-1 - L-i(t)]-1 · M-i(t) · (t) = [li(t) · En-1 - L-i(t)]-1 · M-i(t) · |
й
к
л |
|
B0Mi(t)
mi1(t)
|
- En |
щ
ъ
ы |
· Di[1](t), i =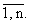 |
|
Таким образом, неопределенной осталась лишь
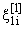 (t). С
учетом результатов, полученных в [1], в качестве
(t). С
учетом результатов, полученных в [1], в качестве
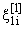 (t)
можно взять некоторую произвольную, необходимое число раз дифференцируемую,
скалярную функцию. Зная xi[1](t), из
(28) легко можно определить и искомый вектор-столбец
ki[1](t):
(t)
можно взять некоторую произвольную, необходимое число раз дифференцируемую,
скалярную функцию. Зная xi[1](t), из
(28) легко можно определить и искомый вектор-столбец
ki[1](t):
Определение членов порядка k = 2,3,.... Пусть найдены все члены
разложений ki(t,e)
и b(t,e) до порядка k - 1 включительно. Тогда таким же путем, как и выше, можно
определить члены порядка k.
Заключение. Из (2), (3) и (4) следует вид для решения системы
(1):
X(t,e) = S(t) · K(t) ·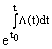 · c, · c, | |
(36) |
где c - вектор-столбец произвольных
постоянных, причем
| L(t) = diag(l1(t),l2(t),...,ln(t)). | |
Вектор-столбец Xm(t,e), определенный
равенством (36), в предположении, что в разложениях ki(t - es,e), q(t - es,e),
exp[qi(t - s,e) - qi(t,e)], q(s,t - es) [1],
а также для (13), (14) берутся лишь члены порядка не выше m относительно e, назовем приближенным решением m-го порядка для системы
(1). Следуя [1], можно доказать, что Xm(t,e)
носит асимптотический характер, т.е. |X(t,e) - Xm(t,e)| Ј em+1 · N, где N - некоторое ограниченное
число.
Государственный инженерный университет
Армении
Ереванский государственный колледж
информатики
Литература
1. Абгарян К. А. Матричные и
асимптотические методы в теории линейных систем. М. Наука 1973. 431 с.
2. Д'Анджело Г. Линейные
системы с переменными параметрами, анализ и синтез. М. Mашиностроение. 1974. 287
с.
3. Bucy R. S. - IEEE.
Transaction on Autimatic Control. 1968. V AC-13. N5. P. 567-569.
4. Chao K. S, Liu D. K. IEEE. - Transaction on Autоmatic Control. 1971. V. AC-16. N1. P. 100-101.
5. Симонян С. О. - Изв. НАН
РА и ГИУА. 2000. T. 53. N3. С. 389-393.
6.
Григорян Ф. П. - Изв. НАН РА и ГИУА. 2002. Т. 55. N1. С. 121-127.
![]() B(t) = (h1(t),h2(t),...,hn(t))T;
b(t) = (b1(t),b2(t),...,bn(t)) и A(t), B(t),
b(tў), g(t - tў,tў) дифференцируемы по своим
аргументам любое необходимое число раз. Требуется построить b(tў) так, чтобы решение системы (1) имело вид
B(t) = (h1(t),h2(t),...,hn(t))T;
b(t) = (b1(t),b2(t),...,bn(t)) и A(t), B(t),
b(tў), g(t - tў,tў) дифференцируемы по своим
аргументам любое необходимое число раз. Требуется построить b(tў) так, чтобы решение системы (1) имело вид ![]() подлежащая определению; li(t), i =
подлежащая определению; li(t), i =![]() - наперед
заданные, необходимое число раз дифференцируемые на
[t0,t1] функции, удовлетворяющие
условиям:
- наперед
заданные, необходимое число раз дифференцируемые на
[t0,t1] функции, удовлетворяющие
условиям:![]()
![]() не
совпадают с нулями и особыми точками передаточной функции
регулятора,
не
совпадают с нулями и особыми точками передаточной функции
регулятора,![]() не
пересекаются хотя бы с одним из собственных значений матрицы A(t), т.е. |ci(t) - lj(t)| > 0, i № j, i,j =
не
пересекаются хотя бы с одним из собственных значений матрицы A(t), т.е. |ci(t) - lj(t)| > 0, i № j, i,j =![]() где ci(t),
i =
где ci(t),
i =![]() - собственные значения матрицы
A(t).
- собственные значения матрицы
A(t).![]() подлежащая определению, причем по аналогии с (3)
подлежащая определению, причем по аналогии с (3) ![]() являются собственными значениями матрицы
U[i](t), а ki[0](t), i =
являются собственными значениями матрицы
U[i](t), а ki[0](t), i =![]() - соответствующими их
собственными векторами.
- соответствующими их
собственными векторами.![]() (t) и M-i(t) - матрицы с размерами n × (n - 1) и
(n - 1) × n соответственно. Тогда матрицы
(t) и M-i(t) - матрицы с размерами n × (n - 1) и
(n - 1) × n соответственно. Тогда матрицы
![]() (t) и
M-i(t) друг с
другом и с матрицами ki[0](t) и
Mi(t) связаны соотношениями
(t) и
M-i(t) друг с
другом и с матрицами ki[0](t) и
Mi(t) связаны соотношениями ![]() матрицы U(i)(t).
матрицы U(i)(t).![]() (t):
(t): ![]() (t). С
учетом результатов, полученных в [1], в качестве
(t). С
учетом результатов, полученных в [1], в качестве
![]() (t)
можно взять некоторую произвольную, необходимое число раз дифференцируемую,
скалярную функцию. Зная xi[1](t), из
(28) легко можно определить и искомый вектор-столбец
ki[1](t):
(t)
можно взять некоторую произвольную, необходимое число раз дифференцируемую,
скалярную функцию. Зная xi[1](t), из
(28) легко можно определить и искомый вектор-столбец
ki[1](t):