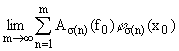МАТЕМАТИКА
УДК 517
А. А. Саргсян
О квазигриди базисности системы Фабера - Шаудерa
(Представлено чл.-кор. НАН РА Г. Г. Гeворкяном 25/V 2005)
Пусть Y =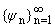 ормированный базис в банаховом пространстве X. Тогда
для каждого элемента f О X существует единственный ряд
по системе
ормированный базис в банаховом пространстве X. Тогда
для каждого элемента f О X существует единственный ряд
по системе
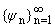 , сходящийся к f по норме пространства X:
, сходящийся к f по норме пространства X:
Пусть элемент f О X задан. Перестановку
натуральных чисел s =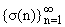 назовем убывающей, если
назовем убывающей, если
| |As(n)(f)| і |As(n+1)(f)|, n = 1,2,... | |
Множество
таких перестановок обозначим через D(f, Y). В случае
строгих неравенств D(f, Y) содержит только одну
убывающую перестановку. Определим m гриди аппроксимант элемента f по базису
Y, отвечающий перестановке s
О D(f,Y) следующим образом:
| Gm(f) = Gm(f, Y, s) = |
m
е
n=1
|
As(n)(f)ys(n). | |
Этот
нелинейный метод аппроксимации известен как гриди алгоритм (см. например [1]).
Гриди алгоритмы для банаховых пространств, относительно нормированных базисов
изучены Конягиным, Темляковым [1], ДеВором [2], Войтащиком [3], Григоряном [4,5]
и др. (см. [6,7]).
Определение
1. Говорят, что гриди алгоритм элемента f О X по системе Y сходится, если
существует s О D(f,Y), для которой
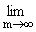 ||Gm(f, Y, s) - f||X = 0 . ||Gm(f, Y, s) - f||X = 0 . | |
(1) |
Если
базис Y является безусловным, то ясно, что
последовательность операторов
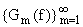 сходится к f О X независимо
от выбора s О D(f, Y).
сходится к f О X независимо
от выбора s О D(f, Y).
Определение 2. Система Y =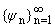 называется квазигриди в X, или квазигриди базисом в
называется квазигриди в X, или квазигриди базисом в
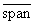 (Y), если для каждого
элемента f О
(Y), если для каждого
элемента f О (Y) и для любой перестановки s О D(f, Y) выполняется
(1).
(Y) и для любой перестановки s О D(f, Y) выполняется
(1).
В работе [2] доказана
следующая
Теорема
[Войтащик]. Для того, чтобы базис Y был квазигриди базисом в X, необходимо и достаточно, чтобы
для каждого элемента f О X, для всякой перестановки
s О D(f, Y) и для любого натурального числа m выполнялось неравенство
| ||Gm(f,
Y, s) ||X Ј
B0 · ||f||X , | |
где
постоянная B0 не зависит от f и от
m.
Напомним определение системы Фабера
- Шаудера. Это система функций F =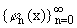 , x О [0,1], в которой
, x О [0,1], в которой
| j0(x) = 1; j1(x) = x; x О [0,1] | |
и
при
n = 2k + i; k = 0, 1, ... ; i = 1, 2, ..., 2k
| jn(x) = j2k+i(x) = jk(i)(x) = |
м
п
п
п
п
н
п
п
п
п
о
|
|
|
| если x
П ( |
i-1
2k
|
, |
i
2k
|
), | |
|
|
|
|
|
| и
непрерывна на [ |
i-1
2k
|
, |
2i-1
2k+1
|
], [ |
2i-1
2k+1
|
, |
i
2k
|
]. | | |
| |
k называется
рангом функции jk(i)(x). Носитель
функции jn(x) , n = 2,3,... системы
(3) обозначим через Dn, а точку, где jn(x) = 1 , n = 2, 3, ..., через
xn.
В работе [7] доказано, что в
пространстве C[0,1] не существует квазигриди базиса. Следовательно, в
случае системы Фабера - Шаудера (система Фабера - Шаудера базис в пространстве
C[0,1], см. [8]) для любого положительного числа B существуют функция
f0 О C[0,1], перестановка s0 О D(f, F) и натуральное число m0, для которых ||Gm0(f0, F, s0 ) ||C > B · ||f0||C.
Отметим,
что доказательство этого результата не имеет конструктивного
характера.
В настоящей работе приведено
конструктивное доказательство этого результата со следующим
усилением:
Теорема 1. Для любого x0,
| x0 О
E0 = |
м
н
о |
3i - 2
3 · 2k
|
, |
3i - 1
3 · 2k
|
; k = 0, 1, ... ; i = 1, 2, ..., 2k |
ь
э
ю |
| |
существуeт
функция f0 О C[0,1], такая что
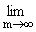 Gm(f0, F, s, x0) = Gm(f0, F, s, x0) =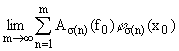 = +Ґ , = +Ґ , |
|
каково
бы ни было s О
D(f0,F).
Пусть S =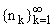 возрастающая последовательность натуральных чисел, а
L (n) - число элементов S меньше n. Положим
возрастающая последовательность натуральных чисел, а
L (n) - число элементов S меньше n. Положим
r(S) =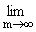 sup
sup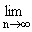 sup
sup
|
L(n + m) - L(n)
m
|
. | |
r(S) называется плотностью множества
S.
Пусть FSў =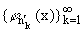 такая подсистема системы (3), что носители функций
jnўk(x), k = 1, 2, ..., попарно не
пересекаются (например FSў =
такая подсистема системы (3), что носители функций
jnўk(x), k = 1, 2, ..., попарно не
пересекаются (например FSў =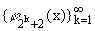 . Очевидно, что FSў является безусловным, следовательно и квазигриди
базисом в замыкании своей линейной оболочки и r(Sў) = 0.
. Очевидно, что FSў является безусловным, следовательно и квазигриди
базисом в замыкании своей линейной оболочки и r(Sў) = 0.
Справедлива
следующая
Теорема 2. Существует подсистема FS
системы Фабера - Шаудера с r(S) = 0, которая не является
квазигриди системой в C[0,1].
Пусть FS =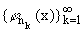 некоторая подсистема системы (2),
S0 =
некоторая подсистема системы (2),
S0 =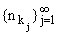 О S некоторое подмножество
множества S и
О S некоторое подмножество
множества S и
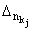 носитель функции
носитель функции
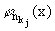 , j = 1, 2, ....
Очевидно, что для всякой S0 =
, j = 1, 2, ....
Очевидно, что для всякой S0 =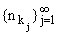 О
S пересечение
О
S пересечение
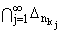 либо пусто, либо точка
отрезка [0,1].
либо пусто, либо точка
отрезка [0,1].
Если
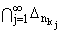 = x0 О [0,1] , то точку x0 назовем точкой сгущения
носителей функций подсистемы FS.
= x0 О [0,1] , то точку x0 назовем точкой сгущения
носителей функций подсистемы FS.
Верна
следующая
Теорема 3. Для того, чтобы подсистема FS =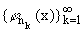 системы (2), являлась квазигриди базисом в замыкании
своей линейной оболочки, необходимо, чтобы носители функций этой подсистемы не
имели точек сгущения в множестве E0.
системы (2), являлась квазигриди базисом в замыкании
своей линейной оболочки, необходимо, чтобы носители функций этой подсистемы не
имели точек сгущения в множестве E0.
Рассмотрим подсистему
|
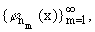
|
(3) |
в которой jn1(x) = j2(x) = j20+1(x) (носителем Dn1 является интервал
(0,1) , xn1 =
1/2) , jn2(x) = j3(x) = j21+1(x) (носителем Dn2 является левая половина интервала
Dn1 , xn2 = 1/4) , jn3(x) = j6(x) = j22+2(x) (носителем Dn3 является правая половина интервала
Dn2 , xn3 = [(1/2+1/4)/2]),
и т.д. Носителем функции jn2m+1(x) является правая половина
интервала Dn2m (xn2m+1 = [(xn2m-1+ xn2m)/2]), а носителем
функции jn2m+2(x) является левая
половина интервала Dn2m+1 (xn2m+2 = [(xn2m+ xn2m+1)/2]) , m = 1, 2, ... .
Нетрудно показать, что все функции подсистемы (3) имеют одно и то же
значение в точке 1/3:
| jnm |
ж
з
и |
1
3
|
ц
ч
ш |
= |
2
3
|
, m = 1, 2, ... . | |
Более
того, нетрудно доказать, что для каждой точки x0 О E0 существуeт подсистема FS =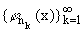 такая, что jnk(x0) = 2/3 , k = 1, 2, ... .
такая, что jnk(x0) = 2/3 , k = 1, 2, ... .
Совокупность
таких подсистем обозначим через
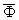 .
.
Ясно, что для каждой
подсистемы
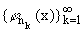 = FS О
= FS О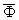 ряд
ряд
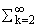 |jnk(x) - jnk-1(x)| сходится в каждой точке x О [0,1].
Положим
|jnk(x) - jnk-1(x)| сходится в каждой точке x О [0,1].
Положим
| L1(x) = |
Ґ
е
k=2
|
|jnk(x) - jnk-1(x)| . | |
При
доказательстве теорем используется следующая
Лемма.
Для каждой подсистемы
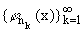 = FS О
= FS О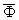 ,
,
Пусть
|
Ґ
е
k=1
|
ak = 1 + |
1
2
|
- |
1
2
|
+ |
1
3
|
+ |
1
4
|
- |
1
4
|
... . | |
(4) |
и A некоторое конечное число. По
схеме Римана переставим члены ряда (4) так, чтобы он сходился к A. Члены
переставленного ряда обозначим через Ak, т.е.
Рассмотрим следующий ряд:
где
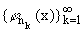 = FS О
= FS О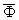 ,
,
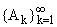 члены ряда
(5). Пусть x0 О [0,1] точка, в которой
функции этой подсистемы принимают значение 2/3. Ясно, что
ряд (6) сходится в каждой точке x О [0,1], так как
члены ряда
(5). Пусть x0 О [0,1] точка, в которой
функции этой подсистемы принимают значение 2/3. Ясно, что
ряд (6) сходится в каждой точке x О [0,1], так как
|
Ґ
е
k=1
|
Akjnk(x0) = |
2
3
|
|
Ґ
е
k=1
|
Ak = |
2
3
|
A, | |
а
при x О [0,1]\{x0} он представляет собой
конечную сумму.
Положим
Проведя
преобразование Абеля и используя лемму , нетрудно показать, что ряд (6) сходится
к f0(x) равномерно.
Пусть
x0 О E0 произвольная точка и
FS =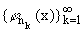 О
О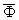 такая подсистема системы (2),
что jnk(x0) = 2/3 ,
k = 1, 2, .... Из равномерной сходимости ряда (6) следует, что
такая подсистема системы (2),
что jnk(x0) = 2/3 ,
k = 1, 2, .... Из равномерной сходимости ряда (6) следует, что
| f0(x) = |
Ґ
е
k=1
|
Akjnk(x) О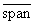 (FS), (FS), |
|
где
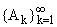 члены ряда
(5). Из построения ряда (6) следует, что при некоторой s О D(f0,FS)
члены ряда
(5). Из построения ряда (6) следует, что при некоторой s О D(f0,FS)
| Gm(f0, FS, s, x0) = |
m
е
k=1
|
As(k)jns(k)(x0) = |
2
3
|
|
m
е
k=1
|
ak. | |
Нетрудно
видеть, что r(S) = 0 и для любой s О D(f0,FS),
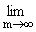 Gm(f0, FS, s, x0) = +Ґ. Gm(f0, FS, s, x0) = +Ґ.
| |
Теоремы доказаны.
В заключение
выражаю благодарность профессору М. Г. Григоряну, под руководством которого
выполнена эта работа.
Ереванский государственный университет
Литература
1. Konyagin S. V., Temlyakov V. N. - East J. on Approx. 1999. V. 5. P. 1-15.
2. De Vore R. A., Temlyakov V. N. - Advances in
Computational Math. 1996. N5. P. 173-187.
3. Wojtaszczyk P. - J. Approx. Theory. 2000. V. 107. P.
293-314.
4. Григорян М. Г. - Изв. НАН Армении. 2004. V. 39. N5. P. 1-14.
5. Grigoryan M. G. - Harmonic analysis and approximations
II. 2003. International conference. Abstrac.
6. Гогян С. Л. - ДНАН Армении. 2005. V. 105. N1. P. 5-9.
7. Dilworth S. J., Kalton N. J., Kutzarova
D. - STUDIA MATHEMATICA. 2003. V. 159(1). P. 67-101.
8. Schauder J. - Math. Zeit.
1927. Bd. 26. S. 47-65.
![]() назовем убывающей, если
назовем убывающей, если ![]() сходится к f О X независимо
от выбора s О D(f, Y).
сходится к f О X независимо
от выбора s О D(f, Y).![]() называется квазигриди в X, или квазигриди базисом в
называется квазигриди в X, или квазигриди базисом в
![]() (Y), если для каждого
элемента f О
(Y), если для каждого
элемента f О![]() (Y) и для любой перестановки s О D(f, Y) выполняется
(1).
(Y) и для любой перестановки s О D(f, Y) выполняется
(1).![]() такая подсистема системы (3), что носители функций
jnўk(x), k = 1, 2, ..., попарно не
пересекаются (например FSў =
такая подсистема системы (3), что носители функций
jnўk(x), k = 1, 2, ..., попарно не
пересекаются (например FSў =![]() . Очевидно, что FSў является безусловным, следовательно и квазигриди
базисом в замыкании своей линейной оболочки и r(Sў) = 0.
. Очевидно, что FSў является безусловным, следовательно и квазигриди
базисом в замыкании своей линейной оболочки и r(Sў) = 0.![]() некоторая подсистема системы (2),
S0 =
некоторая подсистема системы (2),
S0 =![]() О S некоторое подмножество
множества S и
О S некоторое подмножество
множества S и
![]() носитель функции
носитель функции
![]() , j = 1, 2, ....
Очевидно, что для всякой S0 =
, j = 1, 2, ....
Очевидно, что для всякой S0 =![]() О
S пересечение
О
S пересечение
![]() либо пусто, либо точка
отрезка [0,1].
либо пусто, либо точка
отрезка [0,1].![]() = x0 О [0,1] , то точку x0 назовем точкой сгущения
носителей функций подсистемы FS.
= x0 О [0,1] , то точку x0 назовем точкой сгущения
носителей функций подсистемы FS.![]() системы (2), являлась квазигриди базисом в замыкании
своей линейной оболочки, необходимо, чтобы носители функций этой подсистемы не
имели точек сгущения в множестве E0.
системы (2), являлась квазигриди базисом в замыкании
своей линейной оболочки, необходимо, чтобы носители функций этой подсистемы не
имели точек сгущения в множестве E0.
![]() такая, что jnk(x0) = 2/3 , k = 1, 2, ... .
такая, что jnk(x0) = 2/3 , k = 1, 2, ... .![]() .
.![]() = FS О
= FS О![]() ряд
ряд
![]() |jnk(x) - jnk-1(x)| сходится в каждой точке x О [0,1].
Положим
|jnk(x) - jnk-1(x)| сходится в каждой точке x О [0,1].
Положим ![]() = FS О
= FS О![]() ,
,
![]() члены ряда
(5). Пусть x0 О [0,1] точка, в которой
функции этой подсистемы принимают значение 2/3. Ясно, что
ряд (6) сходится в каждой точке x О [0,1], так как
члены ряда
(5). Пусть x0 О [0,1] точка, в которой
функции этой подсистемы принимают значение 2/3. Ясно, что
ряд (6) сходится в каждой точке x О [0,1], так как ![]() О
О![]() такая подсистема системы (2),
что jnk(x0) = 2/3 ,
k = 1, 2, .... Из равномерной сходимости ряда (6) следует, что
такая подсистема системы (2),
что jnk(x0) = 2/3 ,
k = 1, 2, .... Из равномерной сходимости ряда (6) следует, что