МАТЕМАТИКА
УДК 517.53
Академик В. С. Захарян, М. М. Мирзоян
Усиление теоремы Мейера o граничном поведении эквиморфных
функций
(Представлено 6/V 2005)
В настоящей работе усиливается теорема Мейера
([1], с. 204) для эквиморфных в единичном круге D функций по произвольным
касательным путям [2], а также для эквиморфных функций доказываются две теоремы
о свойствах P-последовательности [3,4] и о максимальности предельного множества
теоремы Коллингвуда ([1], с. 108) по произвольным касательным
путям.
1. Пусть D : |z| < 1 - единичный круг, G : |z| = 1 -
единичная окружность, W - сфера Римана (на протяжении
всей работы обозначения D, G и W остаются теми же). Пусть h : D ® D -
такой гомеоморфизм круга D на себя, что отображения h, h-1 равномерно непрерывны относительно гиперболической
метрики единичного круга ds(z) = (1 - |z|2)-1|dz|; s(z1,z2) обозначает расcтояние между
точками z1,z2 О D в
гиперболической метрике. Такие гомеоморфизмы принято называть эквиморфизмами
[5].
В работе Х. Э. Мехия [2] введено понятие
эквиморфной функции и доказано, что множество эквиморфных функций строго
содержит в себе множество квазикoнфoрмных функций
[6].
Эквиморфной функцией называется функция
f : D ® W, которая допускает
представление f = g o h, в котором h : D ® D эквиморфизм и g : D ® W мероморфная функция, нетождественно равная
постоянной.
Пусть x
= etq О G. Для произвольных действительных чисел a и q, 0 < a < Ґ; q і 0, назовем правым q-путем
L+(x,q,a) всякую
кривую, которая задается непрерывной на [0;1) функцией z = z(t) со свойствами:
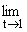 z(t) = x;
|z(t) - x| < z(t) = x;
|z(t) - x| <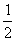 ; q
< argz(t) < q + ; q
< argz(t) < q +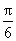 , argz(t) ® 0 (монотонно), , argz(t) ® 0 (монотонно), |
|
при t ® 1 и
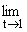 (1 - |z(t)|)|argz(t) - q|-q-1 = a. (1 - |z(t)|)|argz(t) - q|-q-1 = a. | |
Обозначим через L-(x,q,a), 0 < a < Ґ; q і 0, и назовем левым q-путем образ правого q-пути
L+(x,q,a) при
симметрии относительно радиуса h(x,0) круга D в точке
x О G. Правые и левые q-пути назовем q-путями L(x,q,a) (или просто L(x,q)). Для произвольных a > 0,
b > 0, q1 і 0,
q2 і 0, 0 < d
< [1/2] назовем (q1,q2)-углом в точке x О G и
обозначим через D(x,q1,q2,a,b,d) (или
просто D(x,q1,q2), если нас не интересуют
размеры этого угла) подобласть круга D, ограниченную двумя разными L(x,q1,a) и L(x,q2,b) путями (возможeн
случай q1 = q2) и окружностью |z - x| = d, где d
достаточно малое положительное число.
2. Для
произвольной комплекснозначной функции f : D ® W, произвольной точки x О G и произвольного множества S
М D, для которого точка x
является предельной точкой, рассмотрим предельное множество C(f,x,S) функции f в точке x по
множеству S в виде C(f,x,S) =
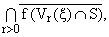 где Vr(x) = {z О D; |z - x| <
r}, r > 0 и черта - замыкание множества. где Vr(x) = {z О D; |z - x| <
r}, r > 0 и черта - замыкание множества. Пусть A - произвольное конечное множество неотрицательных чисел. Точку
x О G
отнесем к множеству PA(f), если каждый q-путь L(x,q) содержит P-последовательность [3] функции f(z). Точку
x О G
отнесем к множеству EA(f), если для любого
(q1,q2)-угла D(x,q1,q2), q1,q2
О A, справeдливо C(f,x,D(x,q1,q2)) = C(f,x,D). Точку x О G отнесем к множеству
KA(f), если для любых двух (q1,q2) и
(q1ў,q2ў)-углов D(x,q1,q2) и D(x,q1ў,q2ў),
q1,q2,q1ў,q2ў О A, имеем C(f,x,D(x,q1,q2)) = C(f,x,D(x,q1ў,q2ў)). Ясно, что EA(f) М
KA(f).
3. Справедлива
следующая
Теорема 1. Пусть f(z) эквиморфная в круге D
функция, f : D ® W, имеет каноническое представление f = g o h.
Тогда q-путь L(x,q) не содержит
P-последовательностей для f(z) в том и только в том случае, когда найдется
(q1,q2)-угол D(x,q1,q2), содержащий L(x,q), в которoм C(Qf,x,D(x,q1,q2)) ограничено, где
| Qf(z) = (1 - |h(z)|2) · |gў(h(z))| · (1 + |g(h(z))|2)-1. | |
Необходимость. Допустим противное, т.е. для любого
(q1,q2)-угла D(x,q1,q2), содержащегo L(x,q), множество C(Qf,x,D(x,q1,q2)) не ограничено. Тогда согласно
лемме 1 из [7] для любого e > 0 существуют такиe
d, 0 < d < 1, и
(q,q)-угол D(x,q,q), что
| L(x,q) З {z; |z - x| < d} М D(x,q,q) М {z О D;s(z;L(x,q)) < e}. | |
Не нарушая общности, будем обозначать q-путь L(x,q) З {z;|z - x| < d} опять символом L(x,q). Но по допущению C(Qf,x,D(x,q,q))
не ограничено. Следовательно, существует последовательность точек
{zn}, zn О D(x,q,q), по которой |
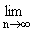 | Qf(zn) = Ґ. Тогда найдется
подпоследовательность {zj} из {zn} такая, что
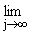 s(zj,L(x,q)) = 0 и s(zj,L(x,q)) = 0 и 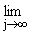 Qf(zj) = Ґ. Qf(zj) = Ґ. |
|
Пусть {zjў} такая последовательность
точек на q-пути L(x,q), для которой
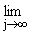 s(zj,zjў) = 0.
Тогда согласно теореме 6 из [2] последовательность точек {zjў} является P-последовательностью для f(z), что невозможно.
Противоречие. s(zj,zjў) = 0.
Тогда согласно теореме 6 из [2] последовательность точек {zjў} является P-последовательностью для f(z), что невозможно.
Противоречие.
Достаточность. Допустим
противное, т.е. по некоторому (q1,q2)-углу D(x,q1,q2),
содержащему q-путь L(x,q), множество
C(Qf,x,D(x,q1,q2)) ограничено и q-путь L(x,q) содержит P-последовательность {zn} для
функции f(z). Тогда согласно лемме 1 из [7] найдется такой угол D(x,q,q), что L(x,q) М D(x,q,q) М
D(x,q1,q2), и значит, множество
C(Qf,x,D(x,q,q)) ограничено. Так как q-путь L(x,q) содержит P-последовательность, то в силу теоремы 4 из
[2] найдется такая последовательность {znў},
|
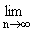 s(zn, znў) = 0,
по которой s(zn, znў) = 0,
по которой
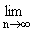 Qf(znў) = Ґ. Начиная с некоторого номера n все точки znў попaдут в (q,q)-угол D(x,q,q), и значит, C(Qf,x,D(x,q,q))
не ограничено. Это противоречие доказывает теорему 1. Qf(znў) = Ґ. Начиная с некоторого номера n все точки znў попaдут в (q,q)-угол D(x,q,q), и значит, C(Qf,x,D(x,q,q))
не ограничено. Это противоречие доказывает теорему 1.
Замечание. В случае, когдa q = 0 и f - мероморфная в D функция, теорема 1
доказана в [8], а в случае, когдa q = 1 и f - мероморфная в D функция, она
усиливает лемму 2 из [9].
4. Справедлива
следующая
Теорема 2. Пусть A - произвольное конечное множество неотрицательных чисел.
Если для эквимоpфной в D функции f : D ® W
в некоторой точке x О KA(f), множествa C(Qf,x,D(x,q1,q2)) ограничены для любого
(q1,q2) - угла, q1,q2 О A, тo для каждого q-пути L(x,q), q
О A, множества C(f,x,L(x,q)) одинaковы и совпадают с множеством C(f,x,D(x,q1,q2)). В частности, если в точке
x О EA(f) множество
C(Qf,x,D) ограничено, то для любого q-пути
L(x,q), q О A, справедливо
| C(f,x,L(x,q)) = C(f,x,D). | |
Замечание. В случае, когдa A = {0} и f - мероморфная в D функция, теорема
2 доказана в работе [8] а в случае, когдa A = {0;1} и f - мероморфная в D функция,
она является усилением леммы 3 из [9].
5.
Пусть f - произвольная функция в круге D и A - произвольное конечное множество
неотрицательных чисел. Точку x О G отнесем к множеству
MA(f), если для произвольного q-пути L(x,q),
q О A, имеем C(f,x,L(x,q)) = C(f,x,D) № W. Точку x О G
отнесeм к множеству IA(f), если для произвольного
(q1,q2)-угла D(x,q1,q2), q1,q2
О A имеем C(f,x,D(x,q1,q2)) = W.
Ясно, что для произвольной функции f : D ® W множества IA(f), MA(f) являются
непересекающимися подмножествами множества
KA(f).
Справедлива следующая
теорема, которая является усилением теоремы 1 из [7].
Теорема 3.
Пусть f произвольная
функция f : D ® W, а A
произвольное конечное множество неотрицательных чисел. Тогда G = EA(f) И F, где F -
множество первой категории и типа Fs
на
G.
Замечание. В
случае, когда A = {0}, теорема 3 доказана Е. П. Долженко ([1], с. 249), в случае,
когда A = {0;1}, она усиливает лемму 1 из [9].
Теорема 4.
Для произвольной
эквиморфной в круге D функции f : D ® W и для произвольного конечного множества A
неотрицательных
чисел справедливо
Для доказательства теоремы 4 достаточно доказать вложение
EA(f) М MA(f)ИIA(f), поскольку обратное вложение следует из
определений участвующих в нем множеств. Рассмотрим произвольную точку x О EA(f), в которой
C(f,x,D) № W. Тогда согласно теореме 4 из [2]
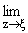 |
supQf(z) < Ґ, z О D, и значит, в силу теоремы 2 x
О MA(f). В случае, когда C(f,x,D) = W, заключаем, что x О IA(f), т.е. теорема 4
доказана.
Замечание. В случае, когда f -
мероморфная в D функция, теорема 4 усиливает лемму 4 из [7], а в случае, когда
A = {0} и f - мероморфная в D функция, она доказана в
[10].
Объединяя результаты теорем 3 и 4,
получаем следующую теорему, которая является усилением теоремы Мейера ([4], с.
204).
Теорема 5. Для произвольной эквиморфной в D
функции f : D ® W и для произвольного конечного
множества A неотрицательных чисел справедливо разложение
где F
- множество первой категории и типа Fs на
G.
Замечание. В
случае, когда f - мероморфная в D функция, теорема 5 усиливает теорему 3 из [7],
в случае, когда A = {0} и f - эквиморфная в D функция, она доказана в работе [2],
в случае, когда A = {0} и f - мероморфная в D функция, - в работе [10], а в
топологических пространствах сходные теоремы доказаны в работах [11-13].
Государственный инженерный университет
Армении Литература
1. Коллингдвуд Э., Ловатер А. Теория предельных множеств. М. Мир. 1971. 312 с.
2. Мехия Х. Э. - ДАН СССР. 1982. T. 265. N1. C.
35-38.
3. Гаврилов В. И. - Матем. сб. 1965. T. 67 (109). N3. C. 408-427.
4. Гаврилов В. И. - Матем. сб. 1966. T. 71 (113).
N3. C. 386-404.
5. Ефремович В. А. - Матем. сб. 1952. Т. 31. Bып. 1. С. 189-200.
6. Lehto O., Virtanen K. I. - Quasiconformal mappings in
the plane. Berlin. Springer-Verlag. 1973.
7. Мирзоян М. М. - ДАН Арм. ССР. 1978. T. 66. N4. C.
200-204.
8. Гаврилов В. И. - ДАН СССР. 1974. T. 216. N1. C. 21-23.
9. Айрапетян А. Н., Гаврилов В. И. - Изв. АН Арм.ССР.
Mатемaтикa. 1976. T. 11. N5. C. 390-399.
10. Гаврилов В. И., Канатинков А. Н. - ДАН ССCР. 1977. T.
233. N1. C. 15-17.
11. Гаврилов В. И.,
Канатинков А. Н. - Математички весник. 1988. (40). Херцег-Нови.
Югославия. C. 217-223.
12. Гаврилов В. И.,
Канатинков А. Н., Кравцев С. В., Симушев А. А. - Математички
весник. 1986. (38). Будва. Югославия. C. 437-450.
13. Абду Аль-Рахман Хасан - ДАН СССР. 1981. T. 260. N4. C.
777-780.
|