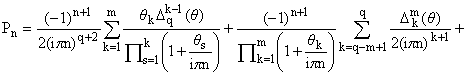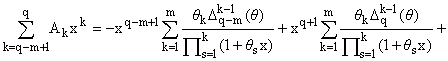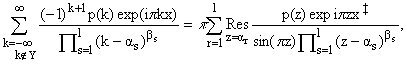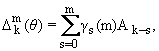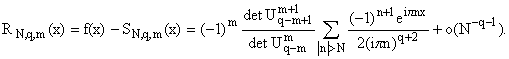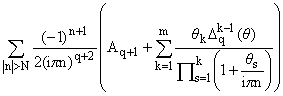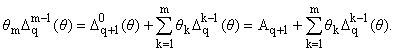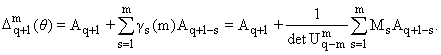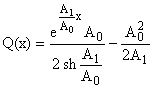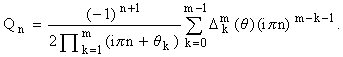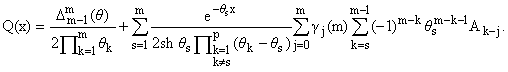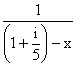МАТЕМАТИКА
УДК 517.518
Академик А. Б. Нерсесян, А. В. Погосян
Асимптотические оценки для одного нелинейного метода
ускоренной
сходимости рядов Фурье
(Представлено 28/II 2005)
1. Хорошо известно, что
классический ряд Фурье на отрезке [a,b],-Ґ < a < b < Ґ, сходится
медленно, если разлагаемая функция f(x), продолженная на всю действительную ось
(b - a) - периодически, не
обладает достаточной гладкостью. Это, прежде всего, относится к кусочно-гладким
функциям.
Решение практически важной проблемы
ускорения сходимости разложений таких функций в ряд Фурье, - по-видимому
впервые, - предложил А. Крылов в 1907 г. (см. [1]). Начало систематическому
обоснованию такого подхода положила в 1964 г. работа [2] Ланцоша (см. также
[3-7]). Практически эффективные алгоритмы были разработаны за последние 15 лет,
главным образом, в работах К. Экгофа и Д. Готтлиба с соавторами (см.,
например, [8-11]).
Упомянутый подход,
связанный с применением полиномов Бернулли (см. ниже, п.2), будем называть
B-методом.
B работе [12] (см. также ниже,
п.3), был разработан другой, нелинейный метод ускорения сходимости рядов Фурье,
основанный на применении аппроксимантов Паде, что привело к еще более точным и
устойчивым алгоритмам. К тому же стало возможным эффективно выявлять колебания
произвольной частоты (в том числе затухающие или нарастающие), являющиеся
"скрытыми" компонентами разлагаемой функции.
Ниже приводятся некоторые теоретические оценки и явные формулы,
связанные с последним подходом.
2. Приведем краткое описание B-метода в случае, когда f О Cp[-1,1]. Рассмотрим
коэффициенты Фурье этой функции
| fn = |
1
2
|
|
у
х |
1
-1
|
f(t)e-ipn tdt, n = 0,±1,±2,ј. | |
(1) |
Интегрированием по частям нетрудно получить следующую асимптотическую формулу
(n № 0):
| fn = |
(-1)n+1
2
|
|
q
е
k=0
|
|
Ak(f)
(ipn)k+1
|
+ |
1
2(ipn)q+1
|
|
у
х |
1
-1
|
f(q+1)(x)e-ipn
xdx, q Ј p-1, | |
(2) |
где обозначено
Ak(f) = f (k)(1) - f (k)(-1), k = 0,ј,q. Если k <
0, то примем Ak = 0.
Рассмотрим
теперь многочлены Бернулли, определяемые рекурpентной формулой
| B0(x) = |
x
2
|
, Bk(x) = |
у
х |
Bk-1(x)dx, x О [-1,1], k = 1,2,ј, | |
где
константа интегрирования вычисляется из условия
 Bk(t)dt = 0, k = 1,2,ј. На всю действительную ось многочлены {Bk(x)}
продолжаются периодически, с периодом 2, и являются кусочно-гладкими функциями с
коэффициентами Фурье Bk,n = 1/2 (-1)n+1/(ipn)k+1, n = 0,±1,±2,ј.
Формула (2) позволяет представить функцию f в виде
Bk(t)dt = 0, k = 1,2,ј. На всю действительную ось многочлены {Bk(x)}
продолжаются периодически, с периодом 2, и являются кусочно-гладкими функциями с
коэффициентами Фурье Bk,n = 1/2 (-1)n+1/(ipn)k+1, n = 0,±1,±2,ј.
Формула (2) позволяет представить функцию f в виде
| f(x) = |
q
е
k=0
|
Bk(x)Ak + F(x), | |
(3) |
где F(x) - некоторая q раз
непрерывно дифференцируемая на действительной оси и 2-периодическая функция.
Очевидно, коэффициенты Фурье {Fn} функции F(x) имеют порядок
убывания, равный, по меньшей мере, o(n-q-1), n ® Ґ. Отсюда следует, что аппроксимационная формула
| SN,q(x) = |
q
е
k=0
|
Bk(x)Ak + |
N
е
n=-N
|
Fneipn x | |
(4) |
сходится к f со скоростью порядка
o(N-q), N ® Ґ.
Обозначим
RN,q(x) = f(x) - SN,q(x). Если q
Ј p - 1, то имеет место
следующая асимптотическая формула:
| RN,q(x) = Aq+1 |
е
|n| >
N
|
|
(-1)n+1
2(ipn)q+2
|
eipn
x + o(N-q-1), N ® Ґ. | |
(5) |
Прикладное значение B-метода
основано на возможности приближенного определения скачков {Ak},
k = 0,1,...,q, решением связанной с формулой (2) линейной системы (см., например,
[10]).
3. Переходя к
описанию метода работы [12], рассмотрим конечную последовательность комплексных
чисел q :=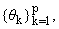 p і 1 и обозначим
p і 1 и обозначим
Если k < 0, то примем
 = 0.
= 0.
Лемма
1. Пусть f О Cp[-1,1] и q Ј p-1. Тогда для любого m і 1 имеет
место следующее разложение (n № 0):
где
|

|
(8) |
| + |
1
2(ipn)q+1
|
|
у
х |
1
-1
|
f (q+1)(t) e-ipntdt. | |
(9) |
Доказательство.
Пользуясь преобразованием Абеля, нетрудно доказать следующее тождество (x №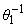 ):
):
|
q
е
k=q-m+1
|
Akxk = xq+1q1 |
Aq - Aq-mx-m
1 + q1x
|
+ |
1
1 + q1x
|
|
q
е
k=q-m+1
|
(Ak + q1Ak-1)xk. | |
(10) |
После m-кратного применения того же преобразования придем к формуле
|

|
(11) |
Доказательство завершается, если
главную часть формулы (2) перепишем в следующей форме:
|
(-1)n+1
2
|
|
q-m
е
k=0
|
|
Ak(f)
(ipn)k+1
|
+ |
(-1)n+1
2
|
|
q
е
k=q-m+1
|
|
Ak(f)
(ipn)k+1
|
| |
и к
последнeй сумме применим преобразование (11) с заменой x на (ipn)-1.
Нам понадобится
также следующий результат.
Лемма 2 [12]. Пусть {as}, s = 1,...,l, 1 Ј l < Ґ - некоторое
конечное множество комплексных чисел и ¡ Н {as} - его
подмножество целых чисел (возможно, пустое). Справедлива формула
где
{bs}, (s = 1,...,l) - множество
положительных целых чисел, p(z) - многочлен степени не выше
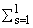 bs-1 и принято
обозначение x‡ = (x + 1) (mod 2) -1, -1 < x‡
< 1.
bs-1 и принято
обозначение x‡ = (x + 1) (mod 2) -1, -1 < x‡
< 1.
Из приведенных лемм следует, что функцию f можно представить в виде
| f(x) = Q(x) + P(x), Q(x) = |
Ґ
е
n=-Ґ
|
Qn ei p n x, P(x) = |
Ґ
е
n=-Ґ
|
Pn ei p n x, | |
(12) |
где Q(x) - квазиполином, т.е.
конечная линейная комбинация из функций вида b(x) ebx, где b(x) - многочлен, b =
const О C. Если же вектор q в разложении (7) определить из системы
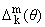 = 0, k = q - m + 1,ј,q, = 0, k = q - m + 1,ј,q, | |
(13) |
то P(x) станет q раз непрерывно
дифференцируемой на действительной оси и 2-периодической функцией. В этом случае
аппроксимационная формула
| SN,q,m(x) = Q(x) + |
N
е
n=-N
|
Pneipn x | |
(14) |
сходится к f со скоростью порядка
o(N-q), N ® Ґ. По сути, мы применили к асимптотическому степенному (по
z = (i p n)-1) ряду (2) аппроксимацию Паде порядка [(q - m)/m] (см. [13]).
Как и в
[12], назовем этот алгоритм квазиполиномиальным (QP) методом.
4. Обозначим теперь
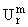 = [Ak-s+r], k, s = 1,ј,m и заметим, что
= [Ak-s+r], k, s = 1,ј,m и заметим, что
где
обозначения gs(m) соответствуют соотношению
|
m
Х
k=1
|
(1 + qk x)
є |
m
е
k=0
|
gk(m)xk. | |
Поэтому
систему (13) можно записать в виде
| Ak+q-m + |
m
е
s=1
|
gs(m)Ak-s+q-m = 0, k = 1,ј,m. | |
(15) |
Она однозначно разрешима, если
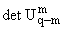 № 0.
№ 0.
Теорема. Если f О
Cq+1[-1,1], f (q+2) О L1[-1,1] и
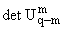 № 0, то имеет место асимптотическая формула (N ® Ґ)
№ 0, то имеет место асимптотическая формула (N ® Ґ)
|
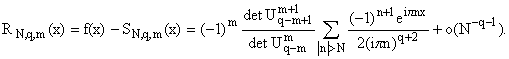
|
(16) |
Доказательство. Из (12) и (14) имеем
| RN, q,m(x) = |
е
|n| >
N
|
Pneipn x. | |
(17) |
Интеграл в правой части (9) можно еще раз проинтегрировать по частям,
поэтому (N ® Ґ)
RN, q,m(x) =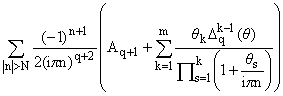 eipn
x + o(N-q-1). eipn
x + o(N-q-1). |
|
(18) |
Отбрасывая члены малого порядка, получим
RN,q,m(x) =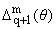 |
е
|n| >
N
|
|
(-1)n+1
2(ipn)q+2
|
eipnx + o(N-q-1), N ® Ґ. | |
(19) |
Здесь мы использовали соотношения (см. (6))
По формулам Крамера gs(m) = Ms /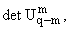 s = 1,ј,m, где {Ms} - соответствующие определители.
Отсюда
s = 1,ј,m, где {Ms} - соответствующие определители.
Отсюда
|
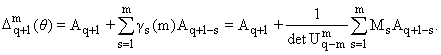
|
(20) |
Разложив теперь определитель
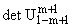 по последней строке, нетрудно заметить, что
выражение (-1)m+2
по последней строке, нетрудно заметить, что
выражение (-1)m+2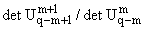 совпадает с
(20).
совпадает с
(20).
5. С помощью леммы
2 нетрудно получить явный вид квазиполинома Q(x). Например при {m,q} = {1,1} и
{m,q} = {1,2} соответственно получим (Ak №
0, k = 0,1,2)
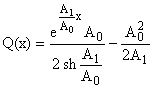 и и

|
|
Опишем случай, когда (как выше слева) Q(x) состоит только из
экспонент.
Пусть f О
Cp[-1,1] и q = 2m - 1, m Ј p/2. К разложению (2)
применим квазидиагональную аппроксимацию Паде порядка [(m-1)/m] (см. (11)).
Предположим, что все {qk} различны и не
равны нулю. Нетрудно убедиться, что в этом случае
|
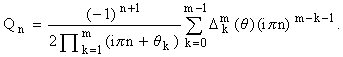
|
Восстановив функцию Q(x) по лемме 2, получим
|
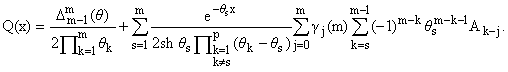
|
(21) |
Эта
формула важна по следующим причинам. Во-первых, в приложениях значения {qk}, k = 1,ј,m
определяются приближенно, как корни соответствующего многочлена (см. [12]).
Понятно, что случай qk = qr, k № r
практически не встречается.
Во-вторых,
формула (21) оптимальна с точки зрения выявления характера "скрытых"
периодичностей функции f(x) (см. [12]).
6. Сравнив формулы (4) и (14), мы видим, что, - при использовании
тех же скачков
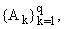 - порядок сходимости
SN,q и SN,q,p к f одинаков. Однако применение предлагаемой
нелинейной аппроксимации потенциально предпочтительней по той простой причине,
что она точная (при достаточно больших q, m и точном определении скачков)
для квазиполиномов, в то время как B-метод точен только для полиномов. Численные
эксперименты полностью подтверждают это преимущество (см. [12]). Конкретная
оценка преимущества QP-метода перед B-методом, основанная непосредственно на
формулах (5) и (6), зависит от скачков {Ak} функции f. Как уже
отмечалось, преимущество это очевидно, если f - квазиполином. В этом случае рост
скачков оценивается как |Ak| Ј
ck, k = 1,2ј; c = const.
Рассмотрим теперь две функции, не являющиеся квазиполиномами:
- порядок сходимости
SN,q и SN,q,p к f одинаков. Однако применение предлагаемой
нелинейной аппроксимации потенциально предпочтительней по той простой причине,
что она точная (при достаточно больших q, m и точном определении скачков)
для квазиполиномов, в то время как B-метод точен только для полиномов. Численные
эксперименты полностью подтверждают это преимущество (см. [12]). Конкретная
оценка преимущества QP-метода перед B-методом, основанная непосредственно на
формулах (5) и (6), зависит от скачков {Ak} функции f. Как уже
отмечалось, преимущество это очевидно, если f - квазиполином. В этом случае рост
скачков оценивается как |Ak| Ј
ck, k = 1,2ј; c = const.
Рассмотрим теперь две функции, не являющиеся квазиполиномами:
f1(x) =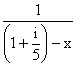 , f2(x) = J0(14x
- 1). , f2(x) = J0(14x
- 1). |
|
(22) |
В
приведенной таблице отношение am(f) = |Aq+1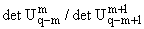 |
характеризует асимптотическое преимущество QP-метода перед B-методом в случае
применения формулы (21) к функциям
f1,f2.
|
характеризует асимптотическое преимущество QP-метода перед B-методом в случае
применения формулы (21) к функциям
f1,f2.
Интересно
сравнить данные табл.1 с приведенными в табл.2 данными, полученными в ходе
эксперимента на компьютере с процессором Pentium 4, 512 RAM c примeнением
системы MATHEMATICA [14]. Здесь приведено полученное из эксперимента отношение
 в равномерной метрике. Как видим, при m Ј 3 данные таблиц практически совпадают. Однако при m і 5 B-метод демонстрирует плохую устойчивость и уступает
QP-методу со все большей (с ростом m) разницей. При m і
7 B-алгоритм становится практически неприменимым.
в равномерной метрике. Как видим, при m Ј 3 данные таблиц практически совпадают. Однако при m і 5 B-метод демонстрирует плохую устойчивость и уступает
QP-методу со все большей (с ростом m) разницей. При m і
7 B-алгоритм становится практически неприменимым.
Таблица 1
Oкругленная теоретическая величина am(f) для
функций f1 и f2 при q = 2m - 1
|
|
|
m = 1 |
m = 2 |
m = 3 |
m = 4 |
m = 5 |
m = 6 |
m = 7 |
m = 8 |
| am(f1) |
2.0 |
6.1 |
20.6 |
72.7 |
2.6 ×102 |
9.6 ×102 |
3.6 ×103 |
1.3 ×104 |
| am(f2) |
0.7 |
42.1 |
30.7 |
271.1 |
2.1 ×102 |
8.6 ×102 |
7.9 ×102 |
2.4 ×103 |
|
Таблица 2
Oкругленная экспериментальная величина
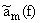 для функций
для функций
f1 и f2 при
q = 2m - 1
|
|
|
m = 1 |
m = 2 |
m = 3 |
m = 4 |
m = 5 |
m = 6 |
m = 7 |
m = 8 |
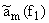 |
2.0 |
6.1 |
20.3 |
42.1 |
6.9 ×104 |
4.8 ·108 |
3.6 ×1011 |
2.2 ×1014 |
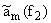 |
0.8 |
40.0 |
34.7 |
399.7 |
2.9 ×104 |
1.5 ×106 |
3.1 ×107 |
3.8 ×108 |
|
Работа
выполнена в рамках проекта ISTC A-823.
Институт математики НАН РА
Литература
1. Крылов А. О приближенных
вычислениях. Типолитогр. К. Биркенфельда. 1907.
2. Lanczos C. - J. Soc. Indust. Appl. Math. Ser. B Numer.
Anal. 1964. V. 1. P. 76-85.
3. Lanczos C. Discourse of Fourier Series. Hafner. N.-Y. 1966.
4. Jones W. B., Hardy G. - Math. Comp. 1970. V. 24. P. 47-60.
5. Lyness J. N. - Math. Comp. 1974. V. 28. P. 81-123.
6. Tasche M. - Math. Nachr.
1979. V. 90. P. 123-134.
7. Baszenski G.,
Delvos F. J., Tasche M. - Computers and Mathematics with
Applications 1995. V. 30. N 3-6. P 33-49.
8. Gottlieb D., Shu C. W. - Math. Comp. 1992. V. 43. P.
81-92.
9. Eckhoff K. S. - Math. Comp. 1995. V. 64. N 210. P. 671 - 690.
10. Eckhoff K. S.,Wasberg C. E. Report no. 99. Dept.
of Math. University of Bergen. 1995. P. 1-38.
11. Gelb A., Gottlieb D. - Computers Math. Applic. 1997.
V. 33. N 11. P. 35-58.
12. Нерсесян А. Б. -
ДНАН Армении. 2004. Т. 104. N. 4. С. 186-191.
13. Бейкер Дж., Грейвс-Моррис П. Аппроксимации Паде. Мир. М. 1986. 502 с.
14. Wolfram S. The MATHEMATICA book. Fourth
Edition. Wolfram Media. Cambridge University Press. 1999. 1468 p.
![]() Bk(t)dt = 0, k = 1,2,ј. На всю действительную ось многочлены {Bk(x)}
продолжаются периодически, с периодом 2, и являются кусочно-гладкими функциями с
коэффициентами Фурье Bk,n = 1/2 (-1)n+1/(ipn)k+1, n = 0,±1,±2,ј.
Формула (2) позволяет представить функцию f в виде
Bk(t)dt = 0, k = 1,2,ј. На всю действительную ось многочлены {Bk(x)}
продолжаются периодически, с периодом 2, и являются кусочно-гладкими функциями с
коэффициентами Фурье Bk,n = 1/2 (-1)n+1/(ipn)k+1, n = 0,±1,±2,ј.
Формула (2) позволяет представить функцию f в виде ![]() p і 1 и обозначим
p і 1 и обозначим ![]() = 0.
= 0.![]() ):
): ![]() bs-1 и принято
обозначение x‡ = (x + 1) (mod 2) -1, -1 < x‡
< 1.
bs-1 и принято
обозначение x‡ = (x + 1) (mod 2) -1, -1 < x‡
< 1.![]() = [Ak-s+r], k, s = 1,ј,m и заметим, что
= [Ak-s+r], k, s = 1,ј,m и заметим, что ![]() № 0.
№ 0.![]() № 0, то имеет место асимптотическая формула (N ® Ґ)
№ 0, то имеет место асимптотическая формула (N ® Ґ) ![]() s = 1,ј,m, где {Ms} - соответствующие определители.
Отсюда
s = 1,ј,m, где {Ms} - соответствующие определители.
Отсюда ![]() по последней строке, нетрудно заметить, что
выражение (-1)m+2
по последней строке, нетрудно заметить, что
выражение (-1)m+2![]() совпадает с
(20).
совпадает с
(20).![]() - порядок сходимости
SN,q и SN,q,p к f одинаков. Однако применение предлагаемой
нелинейной аппроксимации потенциально предпочтительней по той простой причине,
что она точная (при достаточно больших q, m и точном определении скачков)
для квазиполиномов, в то время как B-метод точен только для полиномов. Численные
эксперименты полностью подтверждают это преимущество (см. [12]). Конкретная
оценка преимущества QP-метода перед B-методом, основанная непосредственно на
формулах (5) и (6), зависит от скачков {Ak} функции f. Как уже
отмечалось, преимущество это очевидно, если f - квазиполином. В этом случае рост
скачков оценивается как |Ak| Ј
ck, k = 1,2ј; c = const.
Рассмотрим теперь две функции, не являющиеся квазиполиномами:
- порядок сходимости
SN,q и SN,q,p к f одинаков. Однако применение предлагаемой
нелинейной аппроксимации потенциально предпочтительней по той простой причине,
что она точная (при достаточно больших q, m и точном определении скачков)
для квазиполиномов, в то время как B-метод точен только для полиномов. Численные
эксперименты полностью подтверждают это преимущество (см. [12]). Конкретная
оценка преимущества QP-метода перед B-методом, основанная непосредственно на
формулах (5) и (6), зависит от скачков {Ak} функции f. Как уже
отмечалось, преимущество это очевидно, если f - квазиполином. В этом случае рост
скачков оценивается как |Ak| Ј
ck, k = 1,2ј; c = const.
Рассмотрим теперь две функции, не являющиеся квазиполиномами: ![]() |
характеризует асимптотическое преимущество QP-метода перед B-методом в случае
применения формулы (21) к функциям
f1,f2.
|
характеризует асимптотическое преимущество QP-метода перед B-методом в случае
применения формулы (21) к функциям
f1,f2.![]() в равномерной метрике. Как видим, при m Ј 3 данные таблиц практически совпадают. Однако при m і 5 B-метод демонстрирует плохую устойчивость и уступает
QP-методу со все большей (с ростом m) разницей. При m і
7 B-алгоритм становится практически неприменимым.
в равномерной метрике. Как видим, при m Ј 3 данные таблиц практически совпадают. Однако при m і 5 B-метод демонстрирует плохую устойчивость и уступает
QP-методу со все большей (с ростом m) разницей. При m і
7 B-алгоритм становится практически неприменимым.