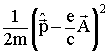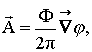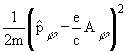ФИЗИКА
УДК 539.2
Р. М. Мовсесян, А. С. Саакян
Одноэлектронные состояния квантового сектора в
ааронов-бомовском магнитном поле
(Представлено академиком А. Р. Мкртчяном 30/VII 2004)
Исследованы одноэлектронные состояния в
2D-секториальной квантовой яме в присутствии ааронов-бомовского магнитного поля.
Показано, что электронные энергетические уровни являются осциллирующими
функциями магнитного потока.
1. Геометрическая форма системы существенно
влияет на спектр элементарных возбуждений [1,2]. Здесь, как и в работe [3],
рассмотрена круговая система радиуса R, состоящая из секториальной квантовой ямы
и смежного с ней барьера. Поведение электронов в этой системе внешне напоминает
известное в квантовой механике падение на центр [4], однако существенно, что
система обладает основным состоянием.
Система находится во внешнем, нормальном к ее
поверхности магнитном поле, локализованном в концентрической круговой области.
Для простоты будем полагать, что размеры области локализации поля одного порядка
с линейным размером вершины сектора (ясно, что вершина сектора не является
идеально заостренной, но имеет конечный размер a) и a << R. Итак,
электроны системы находятся под действием не самого магнитного поля, но
вектор-потенциала. Отмеченное выше упрощение позволяет досконально исследовать
влияние ааронов-бомовского магнитного поля на одно-электронные состояния.
Известно, что в описанной ситуации волновая функция приобретает фазу [5],
пропорциональную магнитному потоку, что фактически разрушает периодичность
системы [6]. Эта ситуация хорошо исследована в полых сверхпроводниках [7] и
металлических баллистических кольцах [8]. Было также показано, что все
макроскопические величины являются осциллирующими функциями магнитного потока
(теорема Байерса - Блоха - Янга [9,10]).
В настоящей работе получены энергетический
спектр и одноэлектронные волновые функции для описанной выше секториальной
системы. Показана осциллирующая зависимость спектра от магнитного потока; в
зависимости от величины потока меняется качественный характер поведения
электрона.
2. Одноэлектронное уравнение Шредингера для
секториальной системы с потоком имеет вид
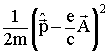 Y
+ UY = EY, Y
+ UY = EY, | |
(1) |
где
с периодическим продолжением в
область j > 2p.
Вектор-потенциал
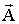 выберем в виде [5]
выберем в виде [5]
j -
полярный угол; F - магнитный поток через область
вершины сектора,
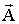 = (Aj,0).
= (Aj,0).
Тогда выполняются следующие условия:
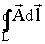 = F, = F, | |
(4a) |
rot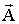 = 0, = 0, |
|
(4b) |
где контур l охватывает область
вершины сектора, а условие (4b) верно во всей области системы кроме области, где
есть магнитное поле.
Для решения уравнения (1) мы используем
адиабатическое приближение, полагая быстрой азимутальную степень свободы.
Волновую функцию Y(r,j) представим в виде
полагая, что y(r,j) удовлетворяет следующему
уравнению:
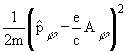 y + Uy = E0y. y + Uy = E0y. | |
(6) |
Состояния, определяемые уравнением (6), имеют блоховский вид
j0 - волновая функция азимутальной степени
свободы, обладающая 2p-периодичностью, а роль
блоховского волнового числа играет отношение a = F/F0, где F0 = ħc/e - элементарный поток.
В интервале [0,2p]
представим волновую функцию y0 в виде
| y0,I = (A1eilj + A2e-ilj)eiaj, | |
| y0,II = (B1emj + B2e-mj)eiaj, | |
где
индексы I и II нумеруют области [0,j0] и
[j0,2p]
соответственно, l =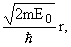 m =
m =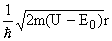 и y0,I, y0,II
удовлетворяют следующим граничным условиям:
и y0,I, y0,II
удовлетворяют следующим граничным условиям:
| yI(j0) = yII(j0),
yўI(j0) = yўII(j0), | |
| yI(0) = yII(2p),
yўI(0) = yўII(2p), | |
которые
с учетом (8) приводят к следующему дисперсионному уравнению для определения
энергетического параметра E0:
| cos(lj0)ch(mb) + |
m2 - l2
2ml
|
sin(lj0)sh(mb) = cos2pa, | |
совпадающего с дисперсионным
уравнением задачи Кронига - Пени.
Из-за трансцендентности уравнение (10) можно
решить в некоторых предельных случаях. Здесь будет рассмотрен наиболее
интересный из них. Пусть одиночная потенциальная яма содержит уровень,
расположенный достаточно близко к ее поверхности e0 Ј U. В случае
бесконечного числа ям этот уровень размывается в зону. В связи с этим решение
ищем в виде
| E0 = e0 - d(a), dmax(a)
<< U. | |
(11) |
Разложим правую часть уравнения (10) в ряд по степеням d, удержав нулевой и линейный по d
члены. В результате уравнение (10) расщепляется на два: решением одного является
| E0 = e0 - |
2ħ2
mbj0r2
|
cos2pa, | |
(12) |
r >>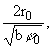 |
r0 =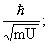 |
|
(12a) |
второе уравнение имеет вид
| th |
rb
R0
|
= |
2r0
R0
|
ctg |
rj0
R0
|
, R0 = |
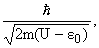 | |
(13) |
решением которого является энергия
локализованного состояния в одиночной яме. В области (12а) оно обладает
следующим решением:
так что окончательно
| E0 = U - |
ħ2
2mb2r2
|
- |
2ħ2
mbj0r2
|
cos2pa. | |
(15) |
Итак, собственные значения энергии азимутальной степени свободы являются
осциллирующими функциями магнитного потока и заполняют "зону" шириной
4ħ2/mbj0r2. Из (15) видно, что в области
значений потока cos2pa <
-(j/2b) зонные
уровни располагаются над ямой; туннелирование с высоко расположенного уровня
приводит к тому, что угловая область локализации электрона становится равной
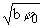 , т.е. в
, т.е. в
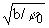 раз
превышает угловой раствор сектора j0.
раз
превышает угловой раствор сектора j0.
Подставив (5) в уравнение (1), умножим слева
на y(r,j) и проинтегрируем по
j; в результате придем к следующему уравнению,
определяющему состояния медленной подсистемы:
| - |
ħ2
2m
|
Dr c + E0(r)c =
Ec +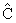 c, c, |
|
(16) |
где Dr - радиальная часть 2D-лапласиана,
E0(r) определяется выражением (15), а
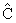 - оператор неадиабатичности имеет следующий вид:
- оператор неадиабатичности имеет следующий вид:
|
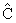 c = c = |
ħ2
2m
|
|
й
к
л |
|
2p
у
х
0
|
y*(Dry)cdj + |
2p
у
х
0
|
y |
¶y
¶r
|
|
¶c
¶r
|
dj |
щ
ъ
ы |
. | |
(17) |
В дальнейшем этим членом
пренебрежем. Обоснование этого приближения дадим позже. Рассматриваем уравнение
| - |
ħ2
2m
|
Dr c + E0(r)c =
Ec, | |
(18) |
или
| r2cўў + rcў + (g - k2r2)c = 0,
| |
| k2 = |
2m(U - E)
ħ
|
, g =
|
4
bj0
|
|
ж
з
и |
|
j0
4b
|
+ cos2pa |
ц
ч
ш |
. | |
(18a) |
Параметр g в (18а), а следовательно, и
сингулярный потенциал E0(r) являются знакопеременными функциями a - притяжение периодически сменяется отталкиванием.
Поведение электронов вблизи вершины сектора существенно зависит от этого
обстоятельства.
Рассмотрим сначала случай g > 0, k2 > 0 (внутриямные состояния).
Волновую функцию можно представить в виде
| c(r) = AJib(ikr) + A*J-ib(-ikr), b = |
Ц
|
g
|
. | |
(19) |
Наложим на волновую функцию (19)
граничные условия
в результате придем к
дисперсионному уравнению
| Jib(ikR)J-ib(ika) - Jib(ika)J-ib(ikR) = 0, | |
(21) |
тогда в приближении ka << 1,
kR >> 1 получим следующее выражение для спектра:
| E = U - |
2ħ2
ma2
|
exp |
м
н
о |
|
1
b
|
|
й
к
л |
2a + p |
ж
з
и |
|
1
2
|
- 2n |
ц
ч
ш |
|
щ
ъ
ы |
|
ь
э
ю |
,
n = 1,2,3,..., | |
(22) |
а волновая функция (19) в
непосредственной близости к вершине имеет вид
| c(r) @ sin |
ж
з
и |
b ln |
r
a
|
|
ц
ч
ш |
, | |
(23) |
внешне совпадающий с волновой
функцией частицы, падающей на центр, однако первое из условий (20) ограничивает
число осцилляций вблизи вершины; этим и обеспечивается существование основного
состояния.
Аналогично можно исследовать
надъямные состояния (g > 0, k2 <
0): волновая функция вблизи вершины имеет вид, совпадающий с (23), а спектр
энергий следующий:
| E = U + |
ħ2
2mR2
|
|
ж
з
и |
j0 - x + b ln2 |
R
a
|
+ pn |
ц
ч
ш |
2
|
, tgx = th |
pb
2
|
, | |
(24) |
близкий к спектру в одномерной яме
бесконечной глубины; это обусловлено вторым из граничных условий (20).
Рассмотрим теперь случай g < 0 ("большой" магнитный поток). Легко показать, что в
этом случае внутриямные состояния отсутствуют, а спектр надъямных состояний
| E = U + |
p2ħ2
2mR2
|
|
ж
з
и |
|
b
2
|
+ |
3
4
|
+ l |
ц
ч
ш |
2
|
. | |
(25) |
В (24) и (25) n и l пробегают
целочисленные значения, а волновая функция в непосредственной близости от
вершины приобретает вид
| c @ sh |
ж
з
и |
b ln |
r
a
|
|
ц
ч
ш |
, | |
(26) |
т.е. осцилляции отсутствуют.
Таким образом, с изменением величины
магнитного потока существенно меняется картина поведения электронов: если в
области g > 0 состояния близки к состояниям с
падением на центр, то в области g < 0 это явление
отсутствует.
Покажем теперь, что оператором
неадиабатичности в уравнении (16) можно пренебречь. Параметр m в (8) в рассматриваемом приближении не зависит от r,
поэтому производные по r обращаются в нуль и в области II
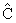 c тождественно равно нулю. В области I, как это легко
показать,
c тождественно равно нулю. В области I, как это легко
показать,
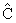 c ~ j02. К адиабатичности системы приводят
два важных обстоятельства: малость j0 и
существование еще одного малого параметра - |U - E0(r)|; благодаря именно
этому условию туннелирование азимутальной степени свободы является быстрым.
c ~ j02. К адиабатичности системы приводят
два важных обстоятельства: малость j0 и
существование еще одного малого параметра - |U - E0(r)|; благодаря именно
этому условию туннелирование азимутальной степени свободы является быстрым.
Государственный инженерный университет
Армении
Литература
1. Андо Т., Фаулер А., Стерн Ф. Электронные свойства двумерных систем. М. Мир. 1985. 380 с.
2. Imry Y. Introduction to
Mesoscopic Physics. Oxford. Univ. Press. 2002. 296 с.
3.
Мовсесян Р. М., Саакян А. С. - Изв. НАН Армении.
Физика. 2004. Т 39. N3. С. 147.
4. Ландау
Л. Д., Лифшиц Е. М. Квантовая механика. М. Наука. 1963. 700 с.
5. Aharonov Y., Bohm D. - Phys. Rev. 1959. V. 115. P. 485.
6. Cheung H-F., Gefen l., Riedel E., Shih W-H. - Phys. Rev.
1988. V. 37. P. 11.
7. Шарвин Д. Ю., Шарвин
Ю. В. - ЖЭТФ. 1965. T. 48. C. 984.
8.
Levi A. F. Physics Today. FEB. 1990. V. 43. P. 58.
9. Byers N., Yang C. N. - Phys. Rev. Lett. 1961. V. 7. N 2.
10. Bloch F. - Phys. Rev. B. 1970. V. 2. N 1.
![]() m =
m =![]() и y0,I, y0,II
удовлетворяют следующим граничным условиям:
и y0,I, y0,II
удовлетворяют следующим граничным условиям: ![]()
![]()
![]()
![]() , т.е. в
, т.е. в
![]() раз
превышает угловой раствор сектора j0.
раз
превышает угловой раствор сектора j0. ![]() c,
c,![]() - оператор неадиабатичности имеет следующий вид:
- оператор неадиабатичности имеет следующий вид: ![]() c =
c = ![]() c тождественно равно нулю. В области I, как это легко
показать,
c тождественно равно нулю. В области I, как это легко
показать,
![]() c ~ j02. К адиабатичности системы приводят
два важных обстоятельства: малость j0 и
существование еще одного малого параметра - |U - E0(r)|; благодаря именно
этому условию туннелирование азимутальной степени свободы является быстрым.
c ~ j02. К адиабатичности системы приводят
два важных обстоятельства: малость j0 и
существование еще одного малого параметра - |U - E0(r)|; благодаря именно
этому условию туннелирование азимутальной степени свободы является быстрым.