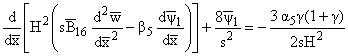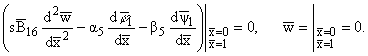МEXAHИКА
УДК 531.8
Г. З. Геворгян, Р. М Киракосян
Уравнения и соотношения анизотропных пластин переменной
толщины при учете поперечных эффектов
(Представлено академиком
C. A. Aмбapцyмяном 30/ХI 2004)
Вопросы уточнения теории пластин постоянной
толщины достаточно обстоятельно и полно рассмотрены в [1-6] и др. Эти вопросы
для многослойных оболочек переменной жесткости обсуждены в [7] и [8]. В [9]
предложен один вариант уравнений и соотношений, учитывающих влияние поперечных
сдвигов, нормального напряжения sz и обжатия
для ортотропных пластин переменной толщины. В настоящей работе приводятся
аналогичные уравнения и соотношения для случая, когда материал имеет лишь одну
плоскость упругой симметрии, параллельную срединной плоскости пластины. Ради
краткости подробности выводов пропущены. Рассмотрен конкретный
пример.
1. Рассмотрим прямоугольную пластину
переменной толщины h(x,y). Совместим координатную плоскость xOy со срединной
плоскостью пластины, направив оси Ox и Oy вдоль сторон пластины, а ось Oz -
вертикально вниз. Материал пластины является линейно упругим и имеет лишь одну
плоскость упругой симметрии, параллельную срединной плоскости. На пластину
действует поверхностная нагрузка, проекции интенсивности которой на координатные
оси, приведенные к единице площади срединной плоскости, составляют X±, Y±, Z±. Знаками "+" и "-" отмечены величины, относящиеся к
поверхностям пластины z = +h/2 и z = -h/2 соответственно.
Условия опирания и нагружения краев пластины
произвольны.
В качестве основного допущения
для построения простейшей теории, учитывающей влияние поперечных эффектов на
расчетные величины рассматриваемой пластины, будем считать, что
| txz = j1 + zj2 + z2j3, tyz = y1 + zy2 + z2y3, | |
(1.1) |
где ji, yi -
искомые функции координат x, y.
По аналогии с
[9] для перемещений и остальных напряжений получим формулы:
| ux = u - z |
ж
з
и |
|
¶w
¶x
|
- a55j1 - a45y1 |
ц
ч
ш |
,
uy = v - z |
ж
з
и |
|
¶w
¶y
|
- a44y1 - a45j1 |
ц
ч
ш |
; | |
(1.2) |
| sx = B11 |
¶u
¶x
|
+ B12 |
¶v
¶y
|
+ B16 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
- A1 |
й
к
л |
Z1 + |
z
4
|
|
ж
з
и |
j2 |
¶h
¶x
|
+ y2 |
¶h
¶y
|
|
ц
ч
ш |
|
щ
ъ
ы |
- | |
| - z |
ж
з
и |
B11 |
¶2w
¶x2
|
+ B12 |
¶2w
¶y2
|
+ 2B16 |
¶2w
¶x¶y
|
- a1 |
¶j1
¶x
|
- b1 |
¶y1
¶x
|
- a2 |
¶j1
¶y
|
- b2 |
¶y1
¶y
|
|
ц
ч
ш |
; | |
| sy = B12 |
¶u
¶x
|
+ B22 |
¶v
¶y
|
+ B26 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
- A2 |
й
к
л |
Z1 + |
h
4
|
|
ж
з
и |
j2 |
¶h
¶x
|
+ y2 |
¶h
¶y
|
|
ц
ч
ш |
|
щ
ъ
ы |
- | |
(1.3) |
| - z |
ж
з
и |
B12 |
¶2w
¶x2
|
+ B22 |
¶2w
¶y2
|
+ 2B26 |
¶2w
¶x¶y
|
- a3 |
¶j1
¶x
|
- b3 |
¶y1
¶x
|
- a4 |
¶j1
¶y
|
- b4 |
¶y1
¶y
|
|
ц
ч
ш |
; | |
| txy = B16 |
¶u
¶x
|
+ B26 |
¶v
¶y
|
+ B66 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
- A3 |
й
к
л |
Z1 + |
h
4
|
|
ж
з
и |
j2 |
¶h
¶x
|
+ y2 |
¶h
¶y
|
|
ц
ч
ш |
|
щ
ъ
ы |
- | |
| - z |
ж
з
и |
B16 |
¶2w
¶x2
|
+ B26 |
¶2w
¶y2
|
+ 2B66 |
¶2w
¶x¶y
|
- a5 |
¶j1
¶x
|
- b5 |
¶y1
¶x
|
- a6 |
¶j1
¶y
|
- b6 |
¶y1
¶y
|
|
ц
ч
ш |
. | |
Здесь
| w1 = A1 |
¶u
¶x
|
+ A2 |
¶v
¶y
|
+ A3 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
- D1 |
й
к
л |
Z1 + |
h
4
|
|
ж
з
и |
j2 |
¶h
¶x
|
+ y2 |
¶h
¶y
|
|
ц
ч
ш |
|
щ
ъ
ы |
; | |
| w2 = - |
1
2
|
|
ж
з
и |
A1 |
¶2w
¶x2
|
+ A2 |
¶2w
¶y2
|
+ 2A3 |
¶2w
¶x¶y
|
- D2 |
¶j1
¶x
|
- D3 |
¶y1
¶y
|
- D4 |
¶j1
¶x
|
- D5 |
¶y1
¶x
|
|
ц
ч
ш |
; | |
u,
v, w - перемещения срединной плоскости по осям x, y, z соответственно. Параметры
Bij выражаются через упругие постоянные материала по известным
формулам [2].
Приняты следующие обозначения:
| Z1 = (Z+ - Z-)/2,
A1 = a13B11 + a23B12 + a36B16,
A2 = a13B12 + a23B22 + a36B26, | |
| A3 = a13B16 + a23B26 + a36B66, | |
| a1 = a55B11 + a45B16 + A1,
a2 = a55B16 + a45B12,
a3 = a55B12 + a45B26 + A2, | |
| a4 = a55B26 + a45B22, a5 = a55B16 + a45B66 + A3,
a6 = a55B66 + a45B26, | |
| b1 = a44B16 + a45B11, b2 = a44B12 + a45B16 + A1,
b3 = a44B26 + a45B12, | |
(1.5) |
| b4 = a44B22 + a45B26 + A2, b5 = a44B66 + a45B16,
b6 = a44B26 + a45B66 + A3, | |
| D1 = a13A1 + a23A2 + a36A3 - a33, D2 = a13a1 + a23a3 + a36a5 - a33, | |
| D3 = a13b2 + a23b4 + a36b6 - a33, D4 = a13a2 + a23a4 + a36a6, D5 = a13b1 + a23b3 + a36b5. | |
С помощью поверхностных условий пластины функции j2, y2, j3, y3
выражаются через u, v, w, j1, y1. Подставляя эти выражения в формулы напряжений
и производя соответствующие интегрирования по толщине пластины, для усилий и
моментов пластины получим:
| Tx = h |
й
к
л |
a7 |
¶u
¶x
|
+ b7 |
¶v
¶y
|
+ l1 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
- aA1 |
ж
з
и |
X2 |
¶h
¶x
|
+ Y2 |
¶h
¶y
|
+ 4Z1 |
ц
ч
ш |
|
щ
ъ
ы |
; | |
| Ty = h |
й
к
л |
a8 |
¶u
¶x
|
+ b8 |
¶v
¶y
|
+ l2 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
- aA2 |
ж
з
и |
X2 |
¶h
¶x
|
+ Y2 |
¶h
¶y
|
+ 4Z1 |
ц
ч
ш |
|
щ
ъ
ы |
; | |
| Sxy = h |
й
к
л |
a9 |
¶u
¶x
|
+ b9 |
¶v
¶y
|
+ l3 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
- aA3 |
ж
з
и |
X2 |
¶h
¶x
|
+ Y2 |
¶h
¶y
|
+ 4Z1 |
ц
ч
ш |
|
щ
ъ
ы |
; | |
| Mx = - |
h3
12
|
|
ж
з
и |
B11 |
¶2w
¶x2
|
+ B12 |
¶2w
¶y2
|
+ 2B16 |
¶2w
¶x¶y
|
- a1 |
¶j1
¶x
|
- a2 |
¶j1
¶y
|
- b1 |
¶y1
¶x
|
- b2 |
¶j1
¶y
|
|
ц
ч
ш |
; | |
| My = - |
h3
12
|
|
ж
з
и |
B12 |
¶2w
¶x2
|
+ B22 |
¶2w
¶y2
|
+ 2B26 |
¶2w
¶x¶y
|
- a3 |
¶j1
¶x
|
- a4 |
¶j1
¶y
|
- b3 |
¶y1
¶x
|
- b4 |
¶j1
¶y
|
|
ц
ч
ш |
; | |
(1.6) |
| Mxy = - |
h3
12
|
|
ж
з
и |
B16 |
¶2w
¶x2
|
+ B26 |
¶2w
¶y2
|
+ 2B66 |
¶2w
¶x¶y
|
- a5 |
¶j1
¶x
|
- a6 |
¶j1
¶y
|
- b5 |
¶y1
¶x
|
- b6 |
¶j1
¶y
|
|
ц
ч
ш |
; | |
| Nx = |
h
3
|
(X1 + 2j1) + |
1
h
|
|
ж
з
и |
Mx |
¶h
¶x
|
+ Mxy |
¶h
¶y
|
|
ц
ч
ш |
; | |
| Ny = |
h
3
|
(Y1 + 2y1) + |
1
h
|
|
ж
з
и |
Mxy |
¶h
¶x
|
+ My |
¶h
¶y
|
|
ц
ч
ш |
. | |
Здесь
| a7 = B11 - aA1d1, b7 = B12 - aA1d2, l1 = B16 - aA1d3, | |
| a8 = B12 - aA2d1, b8 = B22 - aA2d2, l2 = B26 - aA2d3, | |
(1.7) |
| a9 = B16 - aA3d1, b9 = B26 - aA3d2, l3 = B66 - aA3d3, | |
| d1 = B11 |
ж
з
и |
|
¶h
¶x
|
|
ц
ч
ш |
2
|
+ 2B16 |
¶h
¶x
|
|
¶h
¶y
|
+ B12 |
ж
з
и |
|
¶h
¶y
|
|
ц
ч
ш |
2
|
, d2 = B12 |
ж
з
и |
|
¶h
¶x
|
|
ц
ч
ш |
2
|
+ 2B26 |
¶h
¶x
|
|
¶h
¶y
|
+ B22 |
ж
з
и |
|
¶h
¶y
|
|
ц
ч
ш |
2
|
, | |
| d3 = B16 |
ж
з
и |
|
¶h
¶x
|
|
ц
ч
ш |
2
|
+ 2B66 |
¶h
¶x
|
|
¶h
¶y
|
+ B26 |
ж
з
и |
|
¶h
¶y
|
|
ц
ч
ш |
2
|
, a =
|
й
к
л |
4 + A1 |
ж
з
и |
|
¶h
¶x
|
|
ц
ч
ш |
2
|
+ A2 |
ж
з
и |
|
¶h
¶y
|
|
ц
ч
ш |
2
|
+ 2A3 |
¶h
¶x
|
|
¶h
¶y
|
|
щ
ъ
ы |
-1
|
, | |
| X1 = (X+ - X-)/2,
Y1 = (Y+ - Y-)/2,
X2 = X+ + X-,
Y2 = Y+ + Y-,
Z2 = Z+ + Z-. | |
Подставив (1.6) в уравнения равновесия дифференциального элемента
срединной плоскости пластины [2], после некоторых преобразований получим системы
разрешающих уравнений плоской задачи и задачи изгиба.
а) Ситема уравнений плоской задачи
| h |
й
к
л |
a7 |
¶2u
¶x2
|
+ (a9 + l1) |
¶2u
¶x¶y
|
+ l3 |
¶2u
¶y2
|
+ l1 |
¶2v
¶x2
|
+ (b7 + l3) |
¶2v
¶x¶y
|
+ b9 |
¶2v
¶y2
|
|
щ
ъ
ы |
+ | |
| + |
й
к
л |
|
¶(a7h)
¶x
|
+ |
¶(a9h)
¶y
|
|
щ
ъ
ы |
|
¶u
¶x
|
+ |
й
к
л |
|
¶(b7h)
¶x
|
+ |
¶(b9h)
¶y
|
|
щ
ъ
ы |
|
¶v
¶y
|
+ |
й
к
л |
|
¶(l1h)
¶x
|
+ |
¶(l3h)
¶y
|
|
щ
ъ
ы |
|
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
=
| |
| = -X2 + A1 |
¶
¶x
|
|
й
к
л |
ah |
ж
з
и |
X2 |
¶h
¶x
|
+ Y2 |
¶h
¶y
|
+ 4Z1 |
ц
ч
ш |
|
щ
ъ
ы |
+ A3 |
¶
¶y
|
|
й
к
л |
ah |
ж
з
и |
X2 |
¶h
¶x
|
+ Y2 |
¶h
¶y
|
+ 4Z1 |
ц
ч
ш |
|
щ
ъ
ы |
; | |
| h |
й
к
л |
a9 |
¶2u
¶x2
|
+ (a8 + l3) |
¶2u
¶x¶y
|
+ l2 |
¶2u
¶y2
|
+ l3 |
¶2v
¶x2
|
+ (b9 + l2) |
¶2v
¶x¶y
|
+ b8 |
¶2v
¶y2
|
|
щ
ъ
ы |
+ | |
(1.8) |
| + |
й
к
л |
|
¶(a9h)
¶x
|
+ |
¶(a8h)
¶y
|
|
щ
ъ
ы |
|
¶u
¶x
|
+ |
й
к
л |
|
¶(b9h)
¶x
|
+ |
¶(b8h)
¶y
|
|
щ
ъ
ы |
|
¶v
¶y
|
+ |
й
к
л |
|
¶(l3h)
¶x
|
+ |
¶(l2h)
¶y
|
|
щ
ъ
ы |
|
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
=
| |
| = - Y2 + A3 |
¶
¶x
|
|
й
к
л |
ah |
ж
з
и |
X2 |
¶h
¶x
|
+ Y2 |
¶h
¶y
|
+ 4Z1 |
ц
ч
ш |
|
щ
ъ
ы |
+ A2 |
¶
¶y
|
|
й
к
л |
ah |
ж
з
и |
X2 |
¶h
¶x
|
+ Y2 |
¶h
¶y
|
+ 4Z1 |
ц
ч
ш |
|
щ
ъ
ы |
. | |
б) Сиcтема уравнений задачи изгиба
| h2 |
й
к
л |
|
ж
з
и |
B11 |
¶2h
¶x2
|
+ 2B16 |
¶2h
¶x¶y
|
+ B12 |
¶2h
¶y2
|
|
ц
ч
ш |
|
¶2w
¶x2
|
+ |
ж
з
и |
B12 |
¶2h
¶x2
|
+ 2B26 |
¶2h
¶x¶y
|
+ B22 |
¶2h
¶y2
|
|
ц
ч
ш |
|
¶2w
¶y2
|
+ | |
| + 2 |
ж
з
и |
B16 |
¶2h
¶x2
|
+ 2B66 |
¶2h
¶x¶y
|
+ B26 |
¶2h
¶y2
|
|
ц
ч
ш |
|
¶2w
¶x¶y
|
|
щ
ъ
ы |
- h |
м
н
о |
|
й
к
л |
8 + h |
ж
з
и |
a1 |
¶2h
¶x2
|
+ 2a5 |
¶2h
¶x¶y
|
+ a3 |
¶2h
¶y2
|
|
ц
ч
ш |
|
щ
ъ
ы |
|
¶j1
¶x
|
+ | |
| + h |
й
к
л |
|
ж
з
и |
a2 |
¶2h
¶x2
|
+ 2a6 |
¶2h
¶x¶y
|
+ a4 |
¶2h
¶y2
|
|
ц
ч
ш |
|
¶j1
¶y
|
+ |
ж
з
и |
b1 |
¶2h
¶x2
|
+ 2b5 |
¶2h
¶x¶y
|
+ b3 |
¶2h
¶y2
|
|
ц
ч
ш |
|
¶y1
¶x
|
|
щ
ъ
ы |
+ | |
| + |
й
к
л |
8 + h |
ж
з
и |
b2 |
¶2h
¶x2
|
+ 2b6 |
¶2h
¶x¶y
|
+ b4 |
¶2h
¶y2
|
|
ц
ч
ш |
|
щ
ъ
ы |
|
¶y1
¶y
|
|
ь
э
ю |
- 16 |
ж
з
и |
|
¶h
¶x
|
j1 + |
¶h
¶y
|
y1 |
ц
ч
ш |
=
| |
| = 4 |
й
к
л |
3Z2 + h |
ж
з
и |
|
¶X1
¶x
|
+ |
¶Y1
¶y
|
|
ц
ч
ш |
- X1 |
¶h
¶x
|
- Y1 |
¶h
¶y
|
|
щ
ъ
ы |
; | |
| h2 |
й
к
л |
B11 |
¶3w
¶x3
|
+ (B12 + 2B66) |
¶3w
¶x¶y2
|
+ 3B16 |
¶3w
¶x2¶y
|
+ B26 |
¶3w
¶y3
|
- a1 |
¶2j1
¶x2
|
- (a2 + a5) |
¶2j1
¶x¶y
|
- | |
| - a6 |
¶2j1
¶y2
|
- b1 |
¶2y1
¶x2
|
- (b2 + b5) |
¶2y1
¶x¶y
|
- b6 |
¶2y1
¶y2
|
|
щ
ъ
ы |
+ 2h |
й
к
л |
|
ж
з
и |
B11 |
¶h
¶x
|
+ B16 |
¶h
¶y
|
|
ц
ч
ш |
|
¶2w
¶x2
|
+ | |
| + 2 |
ж
з
и |
B16 |
¶h
¶x
|
+ B66 |
¶h
¶y
|
|
ц
ч
ш |
|
¶2w
¶x¶y
|
+ |
ж
з
и |
B12 |
¶h
¶x
|
+ B26 |
¶h
¶y
|
|
ц
ч
ш |
|
¶2w
¶y2
|
- |
ж
з
и |
a1 |
¶h
¶x
|
+ a5 |
¶h
¶y
|
|
ц
ч
ш |
|
¶j1
¶x
|
- | |
| - |
ж
з
и |
a2 |
¶h
¶x
|
+ a6 |
¶h
¶y
|
|
ц
ч
ш |
|
¶j1
¶y
|
- |
ж
з
и |
b1 |
¶h
¶x
|
+b5 |
¶h
¶y
|
|
ц
ч
ш |
|
¶y1
¶x
|
- |
ж
з
и |
b2 |
¶h
¶x
|
+ b6 |
¶h
¶y
|
|
ц
ч
ш |
|
¶y1
¶y
|
|
щ
ъ
ы |
+ 8j1 = 8X1; | |
(1.9) |
| h2 |
й
к
л |
B16 |
¶3w
¶x3
|
+ (B12 + 2B66) |
¶3w
¶x2¶y
|
+ 3B26 |
¶3w
¶x¶y2
|
+ B22 |
¶3w
¶y3
|
- a5 |
¶2j1
¶x2
|
- (a3 + a6) |
¶2j1
¶x¶y
|
- | |
| - a4 |
¶2j1
¶y2
|
- b5 |
¶2y1
¶x2
|
- (b3 + b6) |
¶2y1
¶x¶y
|
- b4 |
¶2y1
¶y2
|
|
щ
ъ
ы |
+ 2h |
й
к
л |
|
ж
з
и |
B16 |
¶h
¶x
|
+ B12 |
¶h
¶y
|
|
ц
ч
ш |
|
¶2w
¶x2
|
+ | |
| + 2 |
ж
з
и |
B66 |
¶h
¶x
|
+ B26 |
¶h
¶y
|
|
ц
ч
ш |
|
¶2w
¶x¶y
|
+ |
ж
з
и |
B26 |
¶h
¶x
|
+ B22 |
¶h
¶y
|
|
ц
ч
ш |
|
¶2w
¶y2
|
- |
ж
з
и |
a5 |
¶h
¶x
|
+ a3 |
¶h
¶y
|
|
ц
ч
ш |
|
¶j1
¶x
|
- | |
| - |
ж
з
и |
a6 |
¶h
¶x
|
+ a4 |
¶h
¶y
|
|
ц
ч
ш |
|
¶j1
¶y
|
- |
ж
з
и |
b5 |
¶h
¶x
|
+ b3 |
¶h
¶y
|
|
ц
ч
ш |
|
¶y1
¶x
|
- |
ж
з
и |
b6 |
¶h
¶x
|
+ b4 |
¶h
¶y
|
|
ц
ч
ш |
|
¶y1
¶y
|
|
щ
ъ
ы |
+ 8y1 = 8Y1. | |
2. Система уравнений плоской задачи (1.8) имеет четвертый порядок, а
система уравнений задачи изгиба (1.9) - шестой. В соответствии с этим на каждой
стороне края пластины необходимо ставить по пять условий: по два условия для
плоской задачи, по три - для задачи изгиба. Эти условия можно сформулировать с
помощью выражений перемещений, усилий и моментов
пластины.
Ради краткости приведем только
условия шарнирного опирания вдоль линий x = 0, z = z0, где -h/2 Ј z0 Ј h/2:
(плоская задача)
| a7 |
¶u
¶x
|
+ b7 |
¶v
¶y
|
+ l1 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
- aA1 |
ж
з
и |
X2 |
¶h
¶x
|
+ Y2 |
¶h
¶y
|
+ 4Z1 |
ц
ч
ш |
= 0,
(Tx = 0), | |
| a9 |
¶u
¶x
|
+ b9 |
¶v
¶y
|
+ l3 |
ж
з
и |
|
¶u
¶y
|
+ |
¶v
¶x
|
|
ц
ч
ш |
- aA3 |
ж
з
и |
X2 |
¶h
¶x
|
+ Y2 |
¶h
¶y
|
+ 4Z1 |
ц
ч
ш |
= 0,
(Sxy = 0); | |
(2.1) |
(задача изгиба)
| B11 |
¶2w
¶x2
|
+ 2B16 |
¶2w
¶x¶y
|
+ B12 |
¶2w
¶y2
|
- a1 |
¶j1
¶x
|
- a2 |
¶j1
¶y
|
- b1 |
¶y1
¶x
|
- b2 |
¶y1
¶y
|
= 0,
(Mx = 0), | |
(2.2) |
| B16 |
¶2w
¶x2
|
+ 2B66 |
¶2w
¶x¶y
|
+ B26 |
¶2w
¶y2
|
- a5 |
¶j1
¶x
|
- a6 |
¶j1
¶y
|
- b5 |
¶y1
¶x
|
- b6 |
¶y1
¶y
|
= 0,
(Mxy = 0), | |
| w + z0w1 + z02w2 = 0,
(uz(0, z0) = 0). | |
Аналогичным образом можно сформулировать и остальные краевые условия.
Нетрудно заметить, что как разрешающие уравнения (1.8), так и граничные условия
(2.1) не содержат величин изгибного характера. В силу этого плоскую задачу можно
решать отдельно, независимо от задачи изгиба. Если ограничиться точностью
порядка h2/l2, где l - характерный размер пластины в
плане, и из выражения uz отбросить член zw1, вносящий в
задачу изгиба поправку порядка h4/l4, то тогда задача
изгиба также становится самостоятельной и ее можно решать
отдельно.
Таким образом, определение
напряженно-деформированного состояния пластины переменной толщины, которая имеет
одну плоскость упругой симметрии, параллельную срединной плоскости, при учете
поперечных сдвигов, нормального напряжения sz и обжатия сводится к нахождению пяти функций u,
v, w, j1, y1. Для этого необходимо проинтегрировать
уравнения плоской задачи (1.8) и задачи изгиба (1.9) при соответствующих краевых
условиях.
3. Для касательных напряжений txz и tyz
окончательно получим:
| txz = |
12z2 - h2
2h2
|
X1 + |
z
h
|
X2 + |
z
h2
|
|
ж
з
и |
Tx |
¶h
¶x
|
+ Sxy |
¶h
¶y
|
|
ц
ч
ш |
+ |
SNx
J
|
+ | |
| + |
h
4J
|
|
ж
з
и |
1 - |
Sh
J
|
|
ц
ч
ш |
|
ж
з
и |
Mx |
¶h
¶x
|
+ Mxy |
¶h
¶y
|
|
ц
ч
ш |
; | |
(3.1) |
| tyz = |
12z2 - h2
2h2
|
Y1 + |
z
h
|
Y2 + |
z
h2
|
|
ж
з
и |
Ty |
¶h
¶x
|
+ Sxy |
¶h
¶y
|
|
ц
ч
ш |
+ |
SNy
J
|
+ | |
|
h
4J
|
|
ж
з
и |
1 - |
Sh
J
|
|
ц
ч
ш |
|
ж
з
и |
My |
¶h
¶x
|
+ Mxy |
¶h
¶y
|
|
ц
ч
ш |
, S = |
h2 - 4z2
8
|
, J = |
h2
12
|
. | |
(3.2) |
Эти формулы совпадают с аналогичными формулами, соответствующими
классической теории пластин переменной толщины. Учет поперечных сдвигов и
обжатия может сказываться только на значениях внутренних усилий и моментов.
Выражения же поперечных касательных напряжений через силовые факторы пластины
остаются без изменений.
4. Рассмотрим длинную
прямоугольную пластинку, толщина которой по длине не изменяется, а по ширине
изменяется линейно. Пластинка свободно оперта вдоль длинных и произвольно
закреплена вдоль коротких сторон. Она несет равномерно распределенную
поверхностную нагрузку, перпендикулярную срединной плоскости. Материал пластинки
в любой точке имеет одну плоскость упругой симметрии, параллельную срединной
плоскости. Очевидно, что на участке, достаточно удаленном от коротких краев,
изогнутую срединную поверхность пластинки можно считать практически
цилиндрической. Ось Oy направим вдоль одной из длинных сторон. Пусть
| h = h0 + h1x,
Z+ = 0, Z- = q, (Z1 = -q/2,
Z2 = q). | |
(4.1) |
Здесь h0 > 0, h1 > h0/l -
заданные постоянные, l - ширина пластинки. Ограничиваясь точностью порядка
h2/l2, рассмотрим только задачу изгиба, считая, что линии
опирания лежат на срединной плоскости. Перейдем к безразмерным величинам:
|
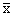 = x/l, = x/l,
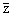 = z/h, s = h0/l,
g = h1/s, = z/h, s = h0/l,
g = h1/s,
| |
(4.2) |
H = h/h0 = 1 + gx, 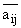 = aij/a11, = aij/a11,
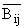 = Bij/B11, = Bij/B11,
|
|
|
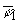
|
= |
j1
q
|
, |
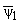
|
= |
y1
q
|
, |
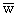
|
= |
wB11
qh0
|
, |
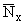
|
= |
Nx
qh0
|
, |
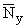
|
= |
Ny
qh0
|
| |
|
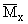
|
= |
Mx
qh02
|
, |
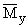
|
= |
My
qh02
|
, |
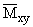
|
= |
Mxy
qh02
|
. | |
В силу статической определимости с учетом (4.1) и (4.2) имеем
|
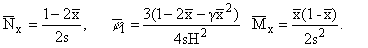
|
(4.3) |
С
учетом (1.6), (1.9), (4.1) и (4.2) задача сводится к интегрированию системы
|
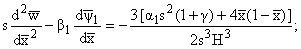 |
(4.4) |
при
краевых условиях
|
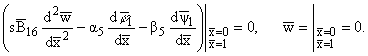
|
(4.5) |
Пусть:
|
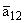
|
= -0.4;
|
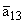
|
= -0.3;
|
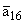
|
= -0.2;
|
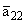
|
= 3; |
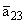
|
= -0.1;
|
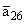
|
= -0.25,
| |
|
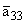
|
= 10; |
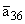
|
= -0.35;
|
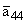
|
= 8; |
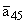
|
= -5;
|
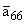
|
= 6; |
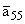
|
= 7; s = 0.1. | |
(4.6) |
Система решается путем разложения в усеченный
степенной ряд степени n функций
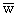 и
и
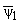 . В качестве
узловых точек взяты корни смещенных многочленов Чебышева
. В качестве
узловых точек взяты корни смещенных многочленов Чебышева
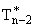 = Tn-2(2x-1). В узловых точках
удовлетворяются уравнения (4.4), а в точках 0 и 1 - краевые условия (4.5).
Вычисления показывают, что при n і 18 значения всех
расчетных величин совпадают с точностью четырех значащих цифр, т.е. с точностью
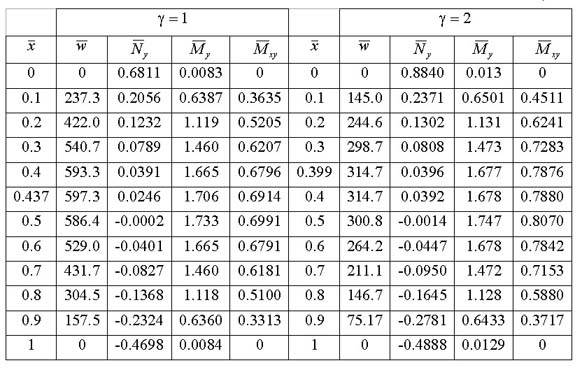
порядка 0.1%. В таблице представлены значения
= Tn-2(2x-1). В узловых точках
удовлетворяются уравнения (4.4), а в точках 0 и 1 - краевые условия (4.5).
Вычисления показывают, что при n і 18 значения всех
расчетных величин совпадают с точностью четырех значащих цифр, т.е. с точностью
порядка 0.1%. В таблице представлены значения
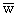 ,
,
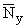 ,
,
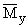 ,
,
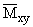 при n = 18 для g = 1 и g = 2 в
равноотстoящих точках и в точках, где
при n = 18 для g = 1 и g = 2 в
равноотстoящих точках и в точках, где
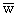 достигает
максимума. Как и следовало ожидать, в отличие от случая ортотропной пластинки, в
данном случае
достигает
максимума. Как и следовало ожидать, в отличие от случая ортотропной пластинки, в
данном случае
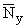 и
и
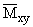 отличны от нуля. Причем момент
отличны от нуля. Причем момент
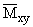 всюду не отрицателен и максимальное значение
принимает при
всюду не отрицателен и максимальное значение
принимает при
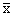 = 0.5. Поперечная же сила
= 0.5. Поперечная же сила
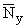 знакопеременна и в сечении
знакопеременна и в сечении
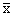 = 0.5 равна нулю. Причем его интеграл по ширине пластинки
для обoих значений g равен
нулю.
= 0.5 равна нулю. Причем его интеграл по ширине пластинки
для обoих значений g равен
нулю.
Институт механики НАН РА
Литература
1. Reissner E. - Trans. ASME.
1945. V. 67. P. A69-A77.
2. Амбарцумян С. А. Теория анизотропных пластин. М. Наука. 1987. 360
с.
3. Власов Б. Ф. - Вестник
МГУ. 1957. №3. С. 42-51.
4. Хачатурян Т. Т.
- Изв. АН Арм ССР. С. физ-мат. наук. 1961. T. 14. №1. С.
67-78.
5. Васильев В. В. - Изв. РАН. МТТ. 1998. №3. С. 46-58.
6. Алфутов Н. А. - Изв. РАН. МТТ. 1992. №3. С.
65-72.
7. Григоренко Я. М., Василенко А. Т. Теория оболочек переменной жесткости. Киев. Наукова Думка. 1981.
544 с.
8. Григоренко Я. М., Василенко А. Т. B сб: Проблемы механики тонких деформируемых тел. Ереван. 2002. С.
155-166.
9. Киракосян Р. М. - Изв. НАН Армении. Mexaникa. 2002. Т. 55. №4. С. 12-23.
![]() и
и
![]() . В качестве
узловых точек взяты корни смещенных многочленов Чебышева
. В качестве
узловых точек взяты корни смещенных многочленов Чебышева
![]() = Tn-2(2x-1). В узловых точках
удовлетворяются уравнения (4.4), а в точках 0 и 1 - краевые условия (4.5).
Вычисления показывают, что при n і 18 значения всех
расчетных величин совпадают с точностью четырех значащих цифр, т.е. с точностью
порядка 0.1%. В таблице представлены значения
= Tn-2(2x-1). В узловых точках
удовлетворяются уравнения (4.4), а в точках 0 и 1 - краевые условия (4.5).
Вычисления показывают, что при n і 18 значения всех
расчетных величин совпадают с точностью четырех значащих цифр, т.е. с точностью
порядка 0.1%. В таблице представлены значения
![]() ,
,
![]() ,
,
![]() ,
,
![]() при n = 18 для g = 1 и g = 2 в
равноотстoящих точках и в точках, где
при n = 18 для g = 1 и g = 2 в
равноотстoящих точках и в точках, где
![]() достигает
максимума. Как и следовало ожидать, в отличие от случая ортотропной пластинки, в
данном случае
достигает
максимума. Как и следовало ожидать, в отличие от случая ортотропной пластинки, в
данном случае
![]() и
и
![]() отличны от нуля. Причем момент
отличны от нуля. Причем момент
![]() всюду не отрицателен и максимальное значение
принимает при
всюду не отрицателен и максимальное значение
принимает при
![]() = 0.5. Поперечная же сила
= 0.5. Поперечная же сила
![]() знакопеременна и в сечении
знакопеременна и в сечении
![]() = 0.5 равна нулю. Причем его интеграл по ширине пластинки
для обoих значений g равен
нулю.
= 0.5 равна нулю. Причем его интеграл по ширине пластинки
для обoих значений g равен
нулю.