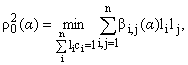СИСТЕМЫ УПРАВЛЕНИЯ
УДК 62.50
В. Р. Барсегян
Задача приоритетного оптимального управления движением и
управляемость линейных систем
(Представлено академиком Ю. Г. Шукуряном 17/II 2005)
Рассматриваются задача приоритетного
оптимального управления движением несколькими управляющими воздействиями и
управляемость линейных систем. Приведены условия вполне управляемости
нестационарной и стационарной систем. Показано, что отдельно по каждому
управляющему воздействию система может быть не вполне управляемой, однако в
совокупности этих управляющих воздействий такая система может стать вполне
управляемой. Для решения задачи приоритетного оптимального управления движением
после построения оптимальных управляющих воздействий проводится минимизация
критерия качества по параметрам, характеризующим приоритетность управляющих
воздействий.
1. Рассмотрим следующую линейную
систему:
|
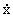 = A(t)x + = A(t)x + |
k
е
i=1
|
aiB(i)(t)u(i), | |
(1.1) |
где x О
Rn, A(t) - (n × n), B(i)(t) - (n × ri)-мерные матрицы, элементы которых измеримые
ограниченные функции, u(i)-ri-мерные вектор-столбцы управляющих воздействий
(i-ый управляющий орган). Предполагается, что управляющие воздействия
u(i) О Pi М Rri, где Pi (i = 1,2,...,k)
- замкнутые ограниченные множества, а параметры ai О [0,1] характеризуют
i-ый орган управления (u(i)) и являются коэффициентами его
приоритетности.
Определение. Систему (1.1) назовем вполне
управляемой на отрезке времени [t0,t1], если из
совокупности {u(1),...,u(k)} управлений могут быть найдены
такие управления, под воздействием которых систему (1.1) можно перевести из
любого начального положения x(t0) в любое конечное положение
x(t1).
Для исследования
управляемости системы (1.1) целесообразно ввести следующие обозначения:
| B(t,a) = (a1B(1)(t),...,akB(k)(t)),
U = |
ж
з
з
з
з
з
и |
|
|
ц
ч
ч
ч
ч
ч
ш |
. | |
(1.2) |
Здесь матрица B(t,a) имеет размерность (n × m),
m =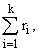 через a обозначена совокупность параметров (a1,...,ak),
размерность вектор-столбца U равна m.
через a обозначена совокупность параметров (a1,...,ak),
размерность вектор-столбца U равна m.
С
учетом введенныx обозначений уравнение (1.1) примет следующий вид:
|
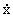 = A(t)x + B(t,a)U. = A(t)x + B(t,a)U. | |
(1.3) |
Предположим, что элементы матриц A(t) и B(t,a)
имеют непрерывные производные по t соответственно вплоть до (n - 2)-ого и (n - 1)-ого порядка по
крайней мере в окрестности некоторой точки t = t* из отрезка
[t0,t1], и в окрестности точки t* введем
матрицы Lk(t,a) следующими рекуррентными
соотношениями:
| L1(t,a) = B(t,a),
Lj(t,a) = A(t)Lj-1(t,a) - |
dLj-1(t,a)
dt
|
(j = 2,...,n). | |
(1.4) |
Согласно [1] имеет место следующая теорема о достаточном условии полной
управляемости для нестационарной системы (1.3).
Теорема 1.
Пусть на отрезке
[t0,t1] существует точка t = t*, в которой ранг
матрицы
| K(t,a) = {L1(t,a),...,Ln(t,a)} | |
(1.5) |
равен n. Тогда
система (1.3) вполне управляема на отрезке
[t0,t1].
Если
система (1.3) стационарна, т.е.
|
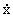 = Ax + B(a)U, = Ax + B(a)U, | |
(1.6) |
то матрица K(t,a), имеющая вид (1.5), согласно (1.4) приобретет следующий
простой вид:
| K(a) = {B(a),AB(a),...,An-1B(a)}. | |
(1.7) |
Теорема 2. Для того чтобы
стационарная система (1.6) была вполне управляемой на любом отрезке
[t0,t1], необходимо и достаточно, чтобы матрица
управляемости K(a) (1.7) имела ранг равный
n.
Доказательство этих теорем аналогичнo
доказательству теорем в [1].
Необходимо
отметить, что при наличии возможности управления системой несколькими
управляющими органами u(i) (i = 1,2,...,k) свойство полной
управляемости приобретает особое значение. Так, в задачах приоритетного выбора
управления, например, при двух управляющих органах, возможно, что система будет
вполне управляемой по одному управляющему органу, а по другому - не вполне
управляемой. Или отдельно по каждому управляющему органу система может быть не
вполне управляемой, однако в совокупности этих двух управляющих органов такая
система может стать вполне управляемой.
Рассмотрим следующую стационарную систему:
|
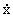 = Ax + a1b(1)u(1) + a2b(2)u(2), = Ax + a1b(1)u(1) + a2b(2)u(2), | |
(1.8) |
где
| A = |
ж
з
и |
a11
a12
a21
a22
|
ц
ч
ш |
,
b(1) = |
ж
з
и |
b1(1)
b2(1)
|
ц
ч
ш |
,
b(2) = |
ж
з
и |
b1(2)
b2(2)
|
ц
ч
ш |
. | |
По каждому управляющему органу (по управлениям u(1) и
u(2), при a1 № 0, a2 № 0) матрицы управляемости имеют вид
| Ki(ai) = |
ж
з
и |
aib1(i)
ai(a11b1(i) + a12b2(i))
aib2(i)
ai(a21b1(i) + a22b2(i))
|
ц
ч
ш |
(i = 1,2), | |
а
по совокупности обоих управляющих органов матрица управляемости будет
| K(a1,a2) = |
ж
з
и |
a1b1(1)
a2b1(2) a1(a11b1(1) + a12b2(1))
a2(a11b1(2) + a12b2(2))
a1b2(1)
a2b2(2) a1(a21b1(1) + a22b2(1))
a2(a21b1(2) + a22b2(2))
|
ц
ч
ш |
. | |
Чтобы система (1.8) по каждому управляющему органу была не вполне
управляемой, а по совокупности обоих органов была вполне управляемой, параметры
этой системы должны удовлетворять следующим условиям:
| rang Ki(ai) №
2, (i = 1,2), rang K(a1,a2) = 2. | |
(1.9) |
В
частности для системы (1.8) справедлива следующая
лемма.
Лемма. Пусть выполнены следующие условия: a11 = a22,
a12 = a21, a11 + a21 № 0, a1 № 0, a2 № 0, b1(1) = -b2(1) № 0,
b1(2) = b2(2) № 0. Тогда система (1.8) по отдельным управлениям
u(1) и u(2) не вполне управляема, а по совокупности
управлений u(1), u(2) вполне
управляема.
Доказательство леммы
проводится непосредственной проверкой условий (1.9).
Примером такой системы является:
|
м
н
о |
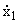 = x1 + 2x2 + a1u1 - a2u2 = x1 + 2x2 + a1u1 - a2u2 | |
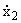 = 2x1 + x2 + a1u1 + a2u2 = 2x1 + x2 + a1u1 + a2u2 | | |
, | |
для которой
матрицы управляемости имеют следующий вид:
| K1(a1) = |
ж
з
и |
a1
3a1
a1 3a1
|
ц
ч
ш |
,
K2(a2) = |
ж
з
и |
-a2 a2
a2 -a2
|
ц
ч
ш |
, K(a1,a2) = |
ж
з
и |
a1
-a2 3a1 a2
a1 a2 3a1 a2
|
ц
ч
ш |
. | |
2. Задачу приоритетного выбора оптимального управления движением
сформулируем следующим образом [2].
Требуется
найти оптимальные управляющие воздействия u(i) на отрезке времени
[t0,t1] и параметры ai
О [0,1] (i = 1,2,...,k), с помощью которых система (1.1)
переводится из заданного начального положения x(t0) в заданное
конечное положение x(t1) и доставляет функционалу
| c[u1,...,uk] = |
ж
з
и |
|
t1
у
х
t0
|
|
k
е
i=1
|
||u(i)||2dt |
ц
ч
ш |
1/2
|
= |
ж
з
и |
|
t1
у
х
t0
|
|
k
е
i=1
|
|
ж
з
и |
|
ri
е
j=1
|
(uj(i))2 |
ц
ч
ш |
dt |
ц
ч
ш |
1/2
|
| |
(2.1) |
наименьшее возможное
значение.
Для решения этой задачи, записывая
формулу Коши для системы (1.1) (или системы (1.3)) и учитывая начальное и
конечное значения фазового вектора, получим следующее интегральное соотношение:
где матрица H[t1,t,a] = X[t1,t]B(t,a) = X[t1,t]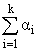 B(i)(t),
X[t1,t] - фундаментальная матрица решений
однородной части системы (1.1), а
B(i)(t),
X[t1,t] - фундаментальная матрица решений
однородной части системы (1.1), а
| C = x(t1) - X[t1,t0]x(t0). | |
(2.3) |
Элементы матрицы H[t1,t,a] линейно зависят от параметров ai
(i = 1,2,...,k).
Учитывая введенные обозначения (1.2), функционал (2.1) можно записать
так:
| c[U] = |
ж
з
и |
|
t1
у
х
t0
|
||U||2dt |
ц
ч
ш |
1/2
|
= |
ж
з
и |
|
t1
у
х
t0
|
|
ж
з
и |
|
m
е
j=1
|
Uj2 |
ц
ч
ш |
dt |
ц
ч
ш |
1/2
|
. | |
(2.4) |
Рассматривая задачу отыскания минимума (2.4) с условием (2.2) как
проблему моментов [1], вычислим
где
| bij(a) = |
m
е
n = 1
|
|
t1
у
х
t0
|
hn(i)[t1,t,a]hn(j)[t1,t,a]dt
(i,j = 1,...,n), | |
h(i)[t1,t,a] - вектор-строка матрицы
H[t1,t,a].
Используя метод
неопределенных множителей Лагранжа, относительно неизвестных
l1,...ln,l, будем иметь систему
алгебраических уравнений
|
n
е
j=1
|
bij(a)lj = -lci,
(i = 1,...,n) | |
(2.6) |
с условием
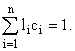
Решение этой системы представится в виде
где
определители Di(a)
получаются из главного определителя det{bij(a)} системы (2.6)
заменой i-ого столбца вектор-столбцом C (2.3).
Имея li0(a), из (2.5)
получим
| r02(a) = |
n
е
i,j=1
|
bij(a)li0(a)lj0(a). | |
Оптимальные управляющие воздействия будут
| Uj0(t,a) = |
1
r02(a)
|
hj(t,a) (j = 1,...,m), где hj(t,a) = |
n
е
i=1
|
li0(a)hij(t1,t,a). | |
Минимальное
значение функционала (2.4) зависит от параметров ai О [0,1]
| c2[U0(a)] = |
1
r02(a)
|
= c2[u(1)0(a1,...,ak),...,u(k)0(a1,...,ak)]. | |
(2.7) |
С
помощью выбора подходящего коэффициента приоритетности органов управления ai (i = 1,2,...,k) можно обеспечить более
минимальное значение для выражения (2.7), т.е.
| c2[u(1)0(a10,...,ak0),...,u(k)0(a10,...,ak0)] =
| |
| = |
min
ai
О [0,1]
|
c2[u(1)0(a1,...,ak),...,u(k)0(a1,...,ak)] (i = 1,...,k). | |
Найденные значения a10,...,ak0 соответствуют приоритетным
оптимальным управляющим воздействиям u(i)0(t,a10,...,ak0), (i = 1,...,k).
Ереванский государственный
университет
Литература
1. Красовский Н. Н. - Теория
управления движением. М. Наука. 1968. 476 с.
2. Габриелян М. С., Барсегян В. Р. - Тезисы докладов. 8-го
междунар. семинарa памяти Е. С. Пятницкого. М. 2004. C. 36-37
![]() через a обозначена совокупность параметров (a1,...,ak),
размерность вектор-столбца U равна m.
через a обозначена совокупность параметров (a1,...,ak),
размерность вектор-столбца U равна m.![]() B(i)(t),
X[t1,t] - фундаментальная матрица решений
однородной части системы (1.1), а
B(i)(t),
X[t1,t] - фундаментальная матрица решений
однородной части системы (1.1), а