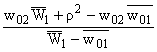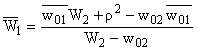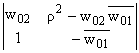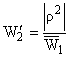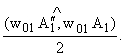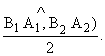ПРИКЛАДНАЯ МАТЕМАТИКА
УДК 62-52 + 513.1
К. А. Согомонян
Плоская бинарная модель четырехмерного пространства и
интерпретация мнимых элементов действительной евклидовой
плоскости
(Представлено академиком А. А. Терзяном 18/Х 2004)
Введение комплексных чисел в алгебру и
развитие учения о мнимом привели к попыткам введения мнимых элементов и в
геометрии. Геометрическую интерпретацию мнимых элементов посредством
действительных образов впервые дал Штаудт в 1860 г. Эта интерпретация приводит к
таким громоздким построениям, что приходится довольствоваться ее принципиальной
возможностью и возвращаться к точке зрения, заключающейся в том, что мнимая
точка есть совокупность комплексных чисел.
Для построения более простой, элементарной и чисто геометрической теории
мнимых образов следовало бы представить основные положения в значительно более
точной и наглядной форме.
Основным объектом
нашего исследования будет вещественно-комплексная плоскость C2,
которая содержит обычную действительную евклидову плоскость R2 в
качестве подмножества. Целью исследования является построение наглядной и с
точки зрения применений простейшей конструктивной модели плоскости C2
в R2, где действительные модели точек, прямых и других образов
плоскости C2, не принадлежащие плоскости R2, будут
изображать мнимые образы плоскости R2.
Известно, что плоскость C2 гомеоморфна вещественному
четырехмерному пространству R4 [1], следовательно, точки плоскости
C2 можно изобразить точками пространства R4. Для этого
будем использовать отображение
где
R4 четырехмерное пространство с ортогональной системой координат x,
y, z, t.
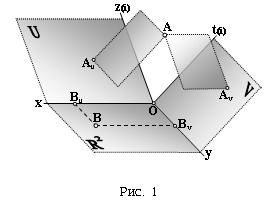
Отображение y осуществляется следующим образом (рис.
1).
Комплексно-координатные прямые плоскости
C2 отображаются плоскостями U = (xz) и V = (yt), в которыe вводится
комплексная структура:
Произвольная точка Aў(Uў,Vў) О
C2 отображается точкой A(x,y,z,t) О
R4, т.е.
| Aў(Uў,Vў) ® A(x,y,z,t); Uў = Au = x + zi, Vў = Av = y + ti, | |
где
точки Au и Av ортогональные проекции точки A О R4 соответственно на координатные плоскости U и
V.
Очевидно, что действительная плоскость
R2 в y отображается на плоскость (xy), и
если Bu О x, Bv О y, то B О R2 -
действительная точка.
Для удобства дальнейших
построений будем использовать комплексный чертеж пространства R4,
представляющий собой набор ортогональных проекций координатных плоскостей (xy),
(xt), (yz), (tz), расположенных на плоскости так, как показано на рис.
2а.
Произвольную точку A О R4 на этом чертеже можно изобразить двумя
произвольными основными проекциями Axt и Ayz. С помощью
этих основных проекций посредством горизонтальных и вертикальных линий связи
можно построить действительную проекцию AR (на плоскость xy ) и чисто
мнимую проекцию Aim (на плоскость tz) этой же
точки.
На этом чертеже изобразим циклические
точки I и J плоскости C2. В C2 эти точки, как известно
[2], являются несобственными точками изотропных прямых. Изотропные прямые,
проходящие через начало координат, определяются уравнениями V = iU и V = -iU.
Отделяя
действительные и мнимые части этих уравнений, получим
|
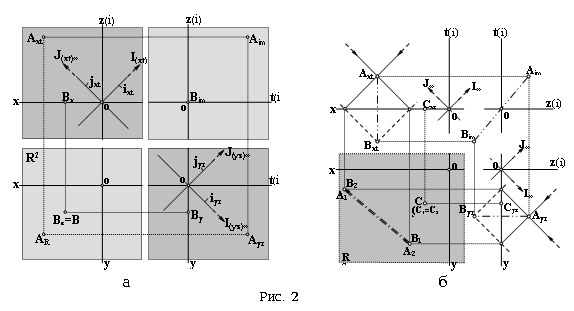
|
которые в
пространстве R4 определяют две взаимно перпендикулярные плоскости.
Они перпендикулярны также основным координатным плоскостям (xt) и (yz). Значит,
на чертеже (рис. 2,а) эти плоскости изобразятся парами основных проекций в виде
прямых линий (ixt,iyz) и (jxt,jyz).
Несобственные точки (I(xt)Ґ,I(yz)Ґ) и (J(xt)Ґ,J(yz)Ґ) этих
проекций на чертеже будут изображать циклические точки комплексной плоскости
C2.
Следующим шагом для получения
требуемой интерпретации является отображение R4 ® R2, которое не может быть взаимно однозначным.
Поэтому будем использовать бинарное проекционное отображение. Исследования
показывают, что наиболее простая интерпретация получается в том случае, когда в
качестве двух центров проецирования выбираются вышеуказанные циклические точки
IҐ и IҐ.
Итак, рассмотрим
бинарное проекционное отображение p(I,J) : R4 ®
R2, в результате которого для произвольной точки A О R4, в качестве интерпретации, в R2
получаем упорядоченную пару проекций (A1,A2), первая из
которых является проекцией точки A из центра IҐ, а вторая - из центра IҐ. Построение этих проекций показано на рис. 2,б. Из
рисунка видно, что та же самая пара проекций с обратной индексацией (например
B1 = A2; B2 = A1) интерпретирует точку
Bў О C2,
сопряженную точке Aў : Bў = s(Aў).
Таким образом, в результате двух отображений y
и p получается требуемая интерпретация: Aў О C2
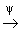 A О
R4 A О
R4 | 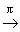 (A1,A2) О R2, в которой любая упорядоченная пара точек
(A1,A2) плоскости R2 интерпретирует
(изображает) определенную мнимую точку этой же
плоскости. (A1,A2) О R2, в которой любая упорядоченная пара точек
(A1,A2) плоскости R2 интерпретирует
(изображает) определенную мнимую точку этой же
плоскости.
Все действительные точки плоскости
R2 естественно считать как совпавшие пары. Например, в случае
C1 = C2 имеем действительную точку, которую можно обозначить
одной буквой C.
Теперь посмотрим, каким
образом на R2 интерпретируются сами центры проецирoвания -
циклические точки I и J. Так как в p точка I является
первым центром проецирования, через который проходят все проецирующие изотропные
прямые, то очевидно, что первой проекцией I можно считать любую точку плоскости
R2. Второй проекцией точки I будет несобственная точка:
I2 = Ґ. Так как J = s(I), то для точки J получаем обратную картину - первая
проекция: J1 = Ґ, а в качестве второй проекции
J2 может служить любая точка плоскости
R2.
Итак, в рассматриваемой
интерпретации в качестве объекта "точка" следует рассматривать произвольную
упорядоченную пару (A1,A2) обычных точек пополненной
плоскости R2, причем:
а) если
A1 № A2, то имеем мнимую "точку"
плоскости R2;
б) если
A1 = A2, то имеем действительную "точку" A О R2;
в) если
A1 = B2, A2 = B1, то
(A1,A2) = s(B1,B2) (мнимо-сопряженные
точки);
г) пара (A1,Ґ) интерпретирует циклическую точку I (A1 -
произвольная);
д) пара (Ґ,A2) интерпретирует циклическую точку J
(A2 - произвольная).
Пусть
проекция A1 в R2 имеет декартовые координаты
x1; y1, а проекция A2 - x2; y2. Пара
(A1,A2) интерпретирует точку Aў(U,V) О C2, где
Нетрудно установить, что отображение Aў | 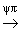 | (A1,A2) определяется
формулами:
| A1 : |
x1 = x + t
y1 = y - z
|
;
A2 : |
x2 = x - t
y2 = y + z
|
. | |
(1) | Обратное отображение определяется формулами:
| U = |
x1 + x2
2
|
+ i |
y2 - y1
2
|
; V = |
y1 + y2
2
|
+ i |
x1 - x2
2
|
. | |
(2) |
В
плоскости R2 вводим комплексную структуру W = x + iy, а проекции
A1 и A2 будем соответственно описывать комплексными
переменными:
| W1 = x1 + iy;
W2 = x2 + iy2, | | тогда
формулы (3) и (4) соответственно примут вид:
|
м
н
о |
W1 = + V + V |
|
W2 = U -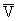 |
| | |
; | |
(3) |
|
м
п
н
п
о
|
U =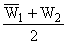 |
|
V =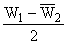 |
| | |
. | |
(4) |
Интерпретация "прямой". В плоскости C2
рассмотрим произвольную прямую V = KU + B, где K,B О C.
Используя формулы (4) отображения C2 | 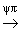 | R2, получим образ этой прямой в
R2 в виде следующего уравнения:
| W2 = |
ж
з
и |
|
i - K
i + K
|
|
ц
ч
ш |
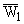
|
- |
2B
i + K
|
. | |
(5) |
Уравнением (5) в R2 определяется некоторое преобразование
j : R2 ®
R2, которое в общем случае является подобием, обращающим ориентацию
плоскости R2, т.е. j О Sim-(R2).
Преобразование j, как известно [3], либо является
скользящей симметрией, либо имеет единственную неподвижную точку w и совпадает с композицией некоторой гомотетии с центром
w и симметрии относительно прямой, проходящей через
w (причем гомотетия и симметрия коммутируют).
Итак:
Каждое подобие j О Sim-(R2) в плоскости R2 интерпретирует некоторую "прямую" плоскости C2,
а каждая пара точек
(A1,A2), где A2 = j(A1), интерпретирует некоторую "точку",
принадлежащую этой прямой.
Если в
R2 совместить начало координатной системы
(x1 = x2; y1 = y2) с точкой w и обозначить: m = [(i - K)/(i + K)]; (m О C), то уравнение (5) примет вид
W2 = m ·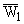 |
, | |
(5*) | что в свою очередь можно
представить как композицию
| W2 = |
m
|m|
|
· |
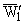
|
. | |
(7) |
Уравнением (6) определяется гомотетия с центром
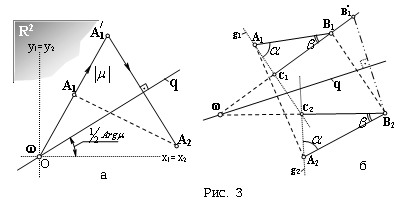
w и коэффициентом |m|, а уравнением (7) - симметрия относительно прямой q, проходящей через w, с угловым коэффициентом tg(1/2 arg m).
Итак, в общем случае
(K;B О C) преобразование j : R2 ® R2,
интерпретирующее "прямую", на R2 конструктивно задается точкой w, осью q и коэффициентом |m| (рис.3,а). Очевидно, что эти
элементы можно задавать с помощью четырех действительных параметров.
Единственной действительной точкой этой "прямой" будет неподвижная точка w, а все остальные, ей принадлежащие мнимые точки
(A1,A2) можно построить следующим
образом.
Для произвольной первой проекции
A1 находим гомотетичную ей точку A1ў: wA1ў = |m| · wA1, а затем получаем
искомую вторую проекцию A2, симметричную точке A1ў относительно оси q.
В
зависимости от коэффициентов (K; B) уравнения (5) получаем следующие частные
случаи:
а) K О R; B
О C. В этом случае |m| = 1, tg(1/2 arg m) = K, имеется единственная несобственная неподвижная точка
wҐ и,
следовательно, преобразование j : R2 ® R2 является скользящей симметрией относительно
оси q.
б) K О R; B
О R. Имеется множество неподвижных точек, заполняющих
всю ось q (|m| = 1, tg(1/2 arg m) = K),
следовательно, преобразование j : R2 ® R2 в этом случае представляет собой обычную
симметрию относительно оси q. Очевидно, только в этом случае "прямая" будет
иметь действительную часть, в виде действительной прямой (q) плоскости
R2.
|
|
Так как j О Sim-(R2) определяется заданием двух
произвольных пар соответствующих точек, любая "прямая" в R2
определяется заданием двух "точек" (мнимых или действительных). Пусть "прямая"
задана двумя произвольными мнимыми точками (A1,A2) и
(B1,B2). Элементы w, q и |m| подобия
j, интерпретирующего заданную "прямую", можно построить
следующим образом (рис. 3,б).
Через точку
A1 проводим прямую g1 параллельно прямой
B1B2 и находим ее образ g2 в j. Для этого достаточно построить равные, но обратно
ориентированные углы
| ( |
A2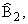 g2 g2
|
) = ( |
A1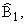 g1 g1
|
) = a. | |
Рассмотрим точку C2 = g1 З g2 и находим ее прообраз C1 в j. Для этого достаточно построить равные, но обратно
ориентированные углы
| ( |
A1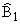 C1 C1
|
) = ( |
A2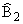 C2 C2
|
) = b. | |
Нетрудно доказать, что прямые B1C1 и
B2C2 пересекаются в искомой неподвижной точке w, ось q представляет собой биссектрису угла
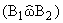 , а коэффициент
гомотетии |m| = [(wB2)/(wB1)] = [(wC2)/(wC1)] = [(wA2)/(wA1)]. , а коэффициент
гомотетии |m| = [(wB2)/(wB1)] = [(wC2)/(wC1)] = [(wA2)/(wA1)].
При
задании "прямой" двумя "точками" необходимо выделить тот частный случай, когда
обе заданные "точки" действительные (A и B). В этом случае имеем множество
неподвижных точек, расположенных на действительной прямой
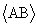 , а j превращается в обычную осевую симметрию относительно этой
же прямой. Очевидно, что в этом случае "прямая" является множеством
мнимосопряженных точек. , а j превращается в обычную осевую симметрию относительно этой
же прямой. Очевидно, что в этом случае "прямая" является множеством
мнимосопряженных точек.
Интерпретация "окружности". В плоскости C2 рассмотрим
произвольную "окружность"
| (U - u0)2 + (V - v0)2 = r2, | |
(8) |
где u0,v0
О C - комплексные координаты центра, а r О C - комплексный радиус. Из
формул (4) перехода C2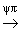 | (R2) получим следующие уравнения:
W2 =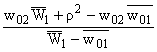 |
|
(9) | или
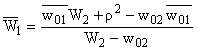 , , | |
(9*) |
которые в R2
определяют интерпретацию "окружности" (8), причем "точка"
(w01,w02), где
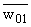 = u0 - iv0; w02 = u0 + iv0,
интерпретирует ее мнимый центр. = u0 - iv0; w02 = u0 + iv0,
интерпретирует ее мнимый центр.
Функция (9)
является однозначной, сопряженно дробнолинейной функцией на полной комплексной
плоскости W є R2, имеющей единственную
особую точку w01 - полюс первого порядка. Обратная функция (9*) также
является однозначной, с особой точкой w02. При этом точка
w01 переходит в точку Ґ, а точка Ґ переходит в точку w02. "Точки"
(w01,Ґ) и (Ґ,w02) интерпретируют циклические точки I,J,
принадлежащие любой "окружности".
Такая
функция, как известно [3], осуществляет конформное преобразование d : R2 ® R2,
обращающее ориентацию плоскости R2, т.е. d
О Conf-(R2). Однозначность преобразования d обеспечивается условием
D =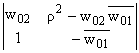 = -r2 №
0. = -r2 №
0. |
|
При D = 0 имеем "окружность" нулевого радиуса,
которая, как известно, представляет собой пару изотропных прямых, проходящих
через ее "центр". В этом случае преобразование d
распадается на два тривиальные соответствия w01 ® R2 и w02 ®
R2, интерпретирующие эти изотропные "прямые" в
R2.
Рассмотрим конструктивные
вопросы задания "окружностей" в R2. Для этого начало координатной
системы в R2 удобно совместить с точкой w01. Тогда
уравнение (9) примет следующий, более простой вид:
W2 =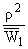 + w02. + w02. |
|
(10) | При
r № 0 уравнение (10) можно
представить в виде
W2 = ei2j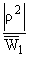 + w02, + w02, |
|
(11) | где j =
arg r.
Полагая
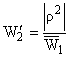 (инверсия радиусом r), получаем (инверсия радиусом r), получаем
W2 = ei2j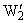 + w02. + w02. | |
(12) |
Значит, d является композицией инверсии (с
центром w01 и радиусом r), вращения (вокруг
w01 на угол 2j) и переноса (на вектор
w01w02).
Итак, в общем
случае (u0,v0,r О C) преобразование d : R2 ® R2,
интерпретирующее "окружность", в R2 конструктивно можно задавать
"центром" (w01,w02) и "радиусом" r (рис. 4,а). Доказывается, что "окружность" в этом случае
может иметь не более двух действительных точек. Принадлежащие ей мнимые точки
(A1,A2) можно построить следующим
алгоритмом:
·
Находим точку Aў1, которая соответствует
произвольно заданной первой проекции A1 в инверсии с центром
w01 и радиусом |r|.
· Вращая точку Aў1 вокруг w01 на угол 2j (j = arg r), находим точку Aўў1.
· Переносом точки Aўў1 на вектор w01w02 находим
искомую проекцию A2.
Когда
"окружность" имеет действительный центр и действительный радиус
(u0,v0,r О R), интерпретирующее еe преобразование d : R2 ® R2
превращается в инверсию относительно этой действительной
окружности.
Любое конформное преобразование
d О Conf-(R2) плоскости R2, как известно,
определяется заданием трех произвольных пар соответствующих точек.
Следовательно, любая "окружность" в R2 определяется заданием трех
"точек" (мнимых или действительных).
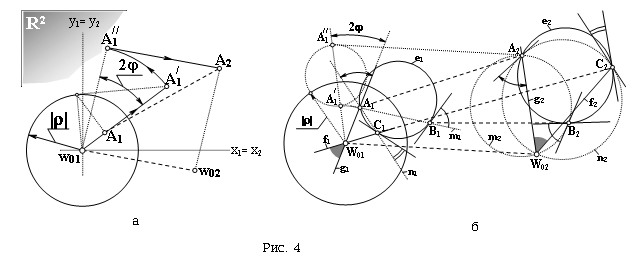
Пусть
"окружность" задана тремя произвольными мнимыми точками
(A1,A2), (B1,B2),
(C1,C2) (рис. 4,б). Тогда "центр"
(w01,w02) и "радиус" r заданной
"окружности" можно построить следующим образом.
· В силу конформности преобразования d очевидно, что окружность e1 (A1,
B1, C1) переходит в окружность e2, проходящyю
через точки A2, B2,
C2.
·
Образом прямой m1 = A1B1 является окружность
m2, которая проходит через A2, B2 и с
окружностью e2 образует угол, равный углу между m1 и
e1.
·
Образом прямой n1 = A1C1 является окружность
n2, которая проходит через A2, C2 и с
окружностью e2 образует угол, равный углу между n1 и
e1.
|
|
·
Точке Ґ, через которую проходят прямые m1 и
n1, соответствует точка w02 = m2 З n2, которая будет второй проекцией искомого
"центра".
· Прямые
g2 = w02A2 и
f2 = w02C2 в преобразовании d-1 переходят в
g1 и f1, построение которых осуществляется с
использованием сохранения углов.
· Точке Ґ, через которую проходят
прямые g2 и f2, в d-1 соответствует точка
w01 = g1 З f1, которая
будет первой проекцией искомого "центра".
· Для определения "радиуса" r (комплексное число) достаточно построить точку
 , перенеся проекцию
A2 на вектор w02w01. Тогда , перенеся проекцию
A2 на вектор w02w01. Тогда
|r| =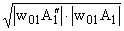 ; Arg r = j = ; Arg r = j =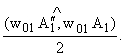 |
|
Метрика. Интерпретацию евклидовой метрики плоскости
C2 в R2 можно получить исходя из интерпретации
"окружности". Действительно, расстояние d между двумя "точками"
(A1,A2), (B1,B2) равно "радиусу"
"окружности" с "центром" (B1,B2), проходящей через "точку"
(A1,A2).
Следовательно,
евклидовым расстоянием d между этими "точками" является комплексное число,
модуль которого равен средней геометрической от длин отрезков
A1B1 и A2B2: |d| =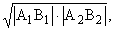 а
аргумент j этого числа равен половине угла между
векторами B1A1 и B2A2: Argd = j = а
аргумент j этого числа равен половине угла между
векторами B1A1 и B2A2: Argd = j =
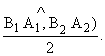
Государственный инженерный университет
Армении
Литература
1. Розенфельд Б. А. Неевклидовы геометрии. М. ГИТТЛ. 1955. 744 с.
2.
Шабат Б. В. Введение в комплексный анализ. М. Наука.
1969. 576 с.
3. Берже М. - Геометрия. 1984. М. Мир. Т. 1. 560 с.
4. Согомонян К. А. Линейно-конструктивные методы
формообразования (геометрическое моделирование). Ереван. Айастан. 1990. 214 с.
5. Согомонян К. А., Туманян К. А., Даллакян
Дж. Н. - Изв. НАН РА и ГИУА. Сер. ТН. 2003. Т. 56. N 3. С.
476-481.
|