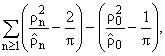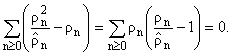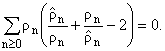МАТЕМАТИКА
УДК 517.9
В. А. Яврян
Об обратной задаче Штурма - Лиувилля на конечном
интервале
(Представлено академиком H. У. Apакeляном 25/II 2005)
1. В пространстве L2(0,p) рассмотрим краевую задачу
| -yўў + q(x)y = ly, x О (0,p) | |
(1) |
где q О
Lp(0,p), (p = 1;2), h, H - вещественные
числа, l - комплексное
число.
Обозначим через j(x,l) решение уравнения (1),
удовлетворяющее условиям
Пусть l0 < l1 < l2
< ... - собственные значения задачи (1)-(3) (иногда их будем обозначать более
подробно ln(q,h,H), n = 0,1,...) и
| rn = rn(q,h,H) = |
ж
з
и |
|
p
у
х
0
|
j2(x,ln)dx |
ц
ч
ш |
-1
|
. | |
Задача восстановления краевой задачи (1)-(3) по двум последовательностям
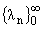 и
и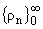 как частный случай обратной задачи по спектральной
функции решена в известной работе И. М. Гельфанда и Б. М. Левитана [1]. Она
подробно изложена в монографиях [2,3] и обзорной статье
[4].
как частный случай обратной задачи по спектральной
функции решена в известной работе И. М. Гельфанда и Б. М. Левитана [1]. Она
подробно изложена в монографиях [2,3] и обзорной статье
[4].
В работах [5,6] условия на
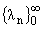 и
и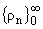 в классе q О
L2(0,p) даны в более явной форме. В этой
статье, развивая метод Гельфанда - Левитана, обобщаются результаты [5,6] для
более естественного класса q О L1(0,p).
в классе q О
L2(0,p) даны в более явной форме. В этой
статье, развивая метод Гельфанда - Левитана, обобщаются результаты [5,6] для
более естественного класса q О L1(0,p).
Лемма
1. Равномерно для x О [0,p] имеем:
| j(x,l) = cos sx + O |
ж
з
и |
|
etx
s
|
|
ц
ч
ш |
, | |
(4) |
| jў(x,l) = -s sin sx + O(etx), | |
(5) |
где s =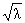 , t = lm s і 0.
, t = lm s і 0.
Существуют такие функции f,g,h О
Lp(0,p), (p = 1;2), что для n > 0
имеем
|
Ц
|
ln
|
= n + |
c
pn
|
+ |
1
n
|
|
p
у
х
0
|
f(t) cos ntdt, | |
(6) |
| rn = |
2
p
|
+ |
1
n
|
|
p
у
х
0
|
g(t) sin ntdt, | |
(7) |
| (-1)nj(p,ln) = 1 + |
1
n
|
|
p
у
х
0
|
h(t)sin ntdt, | |
(8) |
где
| c = h + H + |
1
2
|
|
p
у
х
0
|
q(t)dt. | |
Если вместо краевого условия (3) взять условие
то для собственных значений m0 < m1
< ... задачи (1), (2), (9) будем иметь
|
Ц
|
mn
|
= n + |
1
2
|
+ |
c1
pn
|
+ |
1
n
|
|
p
у
х
0
|
c(t) cos(2n + 1)tdt, n >
0, | |
(10) |
где
| c О Lp(0,p),
c1 = h + |
1
2
|
|
p
у
х
0
|
q(t)dt. | |
Доказательство этой леммы можно получить, если дополнить рассуждения §2
главы 1 из [7] некоторыми несложными выкладками.
С помощью асимптотических формул (6) и (7)
доказывается
Теорема 1. Ряд
|
е
n і 1
|
|
ж
з
и |
rn cos |
Ц
|
ln
|
x - |
2
p
|
cos nx |
ц
ч
ш |
| |
сходится на
[0,2p], его сумма абсолютно непрерывная функция на
[0,2p) и ее производная принадлежит
Lp(0,p),
(p = 1;2).
Пусть
| F(x) = |
е
n і 1
|
|
ж
з
и |
rn cos |
Ц
|
ln
|
x - |
2
p
|
cos nx |
ц
ч
ш |
+ r0 cos |
Ц
|
l0
|
x - |
1
p
|
, x О [0,2p), | |
Обозначим
| f(x,y) = |
1
2
|
|
м
н
о |
F(x + y) + F(|x - y|) |
ь
э
ю |
, x,y О [0,p]. | |
Имеет место соотношение [1]
| K(x,y) + f(x,y) + |
x
у
х
0
|
f(t,y)K(x,t)dt = 0, (0 Ј y Ј x Ј p), | |
(11) |
где K(x,y) - ядро оператора
преобразования для системы (1)-(3):
| j(x,l) = cos |
Ц
|
l
|
x + |
x
у
х
0
|
K(x,y) cos |
Ц
|
l
|
ydy, 0 Ј x Ј p. | |
(12) |
Для
фиксированного x (11) является интегральным уравнением Фредгольма, где
неизвестной является K(x,y). (11) есть известное интегральное уравнение
Гельфанда - Левитана. Из асимптотической формулы (6) следует ([1], §11 или [4],
§6), что уравнение (11) имеет единственное решение для любого x О [0,p]. Можно показать, что K(x,x)
абсолютно непрерывная функция на [0,p] и
q(x) = [1/2][d/dx]K(x,x) О Lp(0,p). Одновремeнно получаем, что
| h = - |
е
n і 1
|
|
ж
з
и |
rn - |
2
p
|
|
ц
ч
ш |
- |
ж
з
и |
r0 - |
1
p
|
|
ц
ч
ш |
, | |
(13) |
| H = - |
е
n і 1
|
|
ж
з
и |
rnj2(p,ln) - |
2
p
|
|
ц
ч
ш |
- |
ж
з
и |
r0j2(p,l0) - |
1
p
|
|
ц
ч
ш |
. | |
(14) |
Таким образом, справедлива
Теорема 2
(oсновная). Пусть последовательности
l0 < l1 < ... и 0 < r0 < r1
< ... удовлетворяют, соответственно, асимптотическим соотношениям (6) и (7),
где c - некоторое число. Тогда существует вещественная функция q О Lp(0,p) и вещественные
числа h и H такие, что ln = ln(q,h,H), rn = rn(q,h,H),
где h и H определяются формулами (13) и (14).
Следствие
1. Чтобы возрастающая последовательность l0 < l1 < ... была последовательностью собственных
значений некоторой краевой задачи (1) - (3), необходимо и достаточно выполнение
асимптотического соотношения (6) при некотором
c.
2. Функция q О Lp(0,p) называется
четной на (0,p) (вернее четной относительно x = [(p)/2]), если q(p-x) = q(x), x О (0,p). Если же, кроме того, H = h, то говорят, что тройка
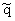 = {q,h,h} - четная. Если
= {q,h,h} - четная. Если
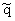 - четная, то очевидно, что вместе с
j(x,ln) собственной
функцией задачи (1)-(3) будет также j(p-x,ln). Отсюда, применяя теорему Штурма о нулях j(x,ln), получаем, что
j(p-x,ln) = (-1)nj(x,ln). При x = 0 имеем
- четная, то очевидно, что вместе с
j(x,ln) собственной
функцией задачи (1)-(3) будет также j(p-x,ln). Отсюда, применяя теорему Штурма о нулях j(x,ln), получаем, что
j(p-x,ln) = (-1)nj(x,ln). При x = 0 имеем
| j(p,ln) = (-1)n,
n = 0,1,2... | |
(15) |
Можно показать, что верно и обратное
утверждение.
Лемма 2. Для четности
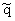 необходимо и достаточно выполнение равенств
(15).
необходимо и достаточно выполнение равенств
(15).
Из формулы Грина легко следует,
что
|
p
у
х
0
|
j2(x,ln)dx = j(p,ln)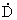 (ln), (ln), |
|
(16) |
где
| D(l) = -(jў(p,l) + Hj(p,l)), | |
а
[D\dot] есть производная D по l.
Таким образом,
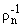 = j(p,ln) = j(p,ln)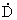 (ln). (ln). |
|
(17) |
Нули целой функции D(l) совпадают с ln, и из теоремы Адамара и оценок (4) и (5)
следует, что
| D(l) = p(l - l0) |
Х
n і 1
|
|
ln - l
n2
|
. | |
Таким образом, D(l) и
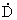 (l) однозначно определяются последовательностью
(l) однозначно определяются последовательностью
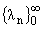 . Из (17) следует
. Из (17) следует
Теорема 3.
Если
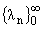 - последовательность собственных значений задачи (1)
- (3) при некотором q0 О
Lp(0,p), h0 и H0, то
существуют четная функция q О Lp(0,p) и число h такие, что ln = ln(q,h,h).
- последовательность собственных значений задачи (1)
- (3) при некотором q0 О
Lp(0,p), h0 и H0, то
существуют четная функция q О Lp(0,p) и число h такие, что ln = ln(q,h,h).
При этом h определяется формулой
| h = - |
е
n і 1
|
|
ж
з
и |
|
1
 |
- |
2
p
|
|
ц
ч
ш |
- |
ж
з
и |
|
1
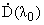 |
- |
1
p
|
|
ц
ч
ш |
. | |
(18) |
Действительно, если
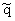 ={q,h,h} - искомая тройка, то из (15) и
(17) следует, что
={q,h,h} - искомая тройка, то из (15) и
(17) следует, что
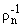 = (-1)n
= (-1)n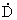 (ln). Следовательно, rn = (-1)n
(ln). Следовательно, rn = (-1)n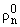 j0(p,ln).
j0(p,ln).
Из (7) и
(8) следует, что rn удовлетворяет (7). Тогда
из теоремы 2 и леммы 2 следует, что существуют четная функция q и число h такие,
что ln = ln(q,h,h). Формула (18) следует из
(13).
В. Амбарцумян в [8] доказал теорему о
том, что если h = H = 0 и ln = n2
(n = 0,1,2,...), то q(x) = 0. Она получила свое обобщение лишь спустя 54 года в
замечательных работах [5] и [6]. Мы доказываем более общую
теорему.
Теорема 4. Если q О L1(0,p),
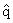 О L1(0,p), q - четная функция, то из
О L1(0,p), q - четная функция, то из
ln(q,h,h) = ln(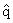 ,h,h),
(n = 0,1,2,...) ,h,h),
(n = 0,1,2,...) |
|
следует, что q(x) =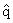 (x) почти всюду в [0,p].
(x) почти всюду в [0,p].
Следствие 2. Если
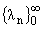 удовлeтворяет условию (6), то существует такое число
h (оно определяется формулой (18)), что из ln(r,h,h) = ln,
(n = 0,1,2,...) функция r О L1(0,p) определяется единственным образом. Эта функция оказывается
четной.
удовлeтворяет условию (6), то существует такое число
h (оно определяется формулой (18)), что из ln(r,h,h) = ln,
(n = 0,1,2,...) функция r О L1(0,p) определяется единственным образом. Эта функция оказывается
четной.
Приведем схему доказательства
теоремы 4. Из (13) следует, что
|
е
n і 1
|
(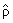 - rn) = - rn) = |
е
n і 1
|
rn |
ж
з
и |
|
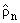
rn
|
-1 |
ц
ч
ш |
= 0. | |
(19) |
Так
как q - четная, то из леммы 2, равенства (17) следует, что
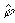 (p,ln) = (-1)nrn
(p,ln) = (-1)nrn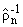 . Отсюда
и из (14), учитывая, что h = H, получаем
. Отсюда
и из (14), учитывая, что h = H, получаем
h =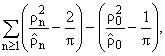 |
|
что
вместе с (13) дает
|
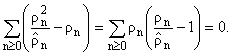
|
(20) |
После сложения (19) и (20) получаем
Так как каждое слагаемое в этом равенстве неотрицательное и rn > 0, то следует, что
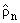 = rn
(n = 0,1,2,...) и из условия теоремы 4 и теоремы Марченко о единственности
получаем, что
= rn
(n = 0,1,2,...) и из условия теоремы 4 и теоремы Марченко о единственности
получаем, что
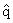 (x) = q(x) почти всюду.
(x) = q(x) почти всюду.
В
работах [5] и [6] результаты п. 2 установлены для q О
L2(0,p).
3. Приведем одно применение теоремы 3.
Рассмотрим уравнение (1) на интервале (0,[(p)/2]) и краевые условия на правом конце:
Пусть
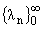 - последовательность собственных значений задачи
(1)-(3), где q - четная и q О Lp(0,p). Тогда j(p - x,ln) = (-1)nj(x,ln). Отсюда следует,
что j([(p)/2],l2n+1) = 0 и jў([(p)/2],l2n) = 0. Это означает, что
- последовательность собственных значений задачи
(1)-(3), где q - четная и q О Lp(0,p). Тогда j(p - x,ln) = (-1)nj(x,ln). Отсюда следует,
что j([(p)/2],l2n+1) = 0 и jў([(p)/2],l2n) = 0. Это означает, что
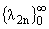 и
и
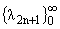 являются, соответственно, собственными значениями
краевых задач (1), (2), (21) и (1), (2), (22). Отсюда с помощью следствия 1 и
теоремы 3 можно доказать следующее утверждение.
являются, соответственно, собственными значениями
краевых задач (1), (2), (21) и (1), (2), (22). Отсюда с помощью следствия 1 и
теоремы 3 можно доказать следующее утверждение.
Теорема 5.
Пусть возрастающие
последовательности
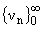 и
и
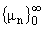 перемежаются:
перемежаются:
и удовлетворяют
асимптотическим формулам
|
Ц
|
nn
|
= n + |
c1
n
|
+ |
1
n
|
|
p
у
х
0
|
f1(t) cos ntdt, | |
|
Ц
|
mn
|
= n + |
1
2
|
+ |
c1
n
|
+ |
1
n
|
|
p
у
х
0
|
c1(t) cos 2n + 1tdt, | |
где
f1,c1 О
Lp(0,p), а c1 - некоторое число.
Тогда существуют q О Lp(0,p) и число h
такие, что
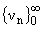 и
и
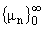 совпадают с собственными значениями задач (1), (2),
(3) с H = 0 и (1), (2), (9), соответственно.
совпадают с собственными значениями задач (1), (2),
(3) с H = 0 и (1), (2), (9), соответственно.
Следствие 3.
Чтобы возрастающая
последовательность
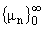 была последовательностью собственных значений
некоторой краевой задачи (1), (2), (9), необходимо и достаточно выполнение
асимптотического соотношения (10) при некотором c1.
была последовательностью собственных значений
некоторой краевой задачи (1), (2), (9), необходимо и достаточно выполнение
асимптотического соотношения (10) при некотором c1.
Ереванский государственный университет
Литература
1. Гельфанд И. М. , Левитан Б.
М. - Изв. АН АрмССР. Математика. 1951. T. 15. C. 309 - 360.
2. Марченко В. А. Операторы Штурма - Лиувилля и их приложения. Киев. Наукова Думка. 1977.
3. Левитан Б. М. Обратные задачи Штурма - Лиувилля. М. Наука. 1984.
4. Левитан Б. М., Гасымов М.
Г. - УМН. 1964. T. 19. Bып. 2(116). C. 3-63.
5. Isaakson E. L., Trubowitz -
Pure Appl. Math. 1983. V. 36. N 6. P. 763-783.
6. Isaakson E. L., McKean H.
P., Trubowitz - Pure Appl. Math. 1984. V. 37. N 1. P.
1-12.
7. Левитан Б. М., Саргсян
И. С. Введение в спектральную теорию. М. Наука. 1970.
8. Ambarzumian V. A. - Z. Physik. 1929. B. 53. S. 690-695.
![]() и
и![]() как частный случай обратной задачи по спектральной
функции решена в известной работе И. М. Гельфанда и Б. М. Левитана [1]. Она
подробно изложена в монографиях [2,3] и обзорной статье
[4].
как частный случай обратной задачи по спектральной
функции решена в известной работе И. М. Гельфанда и Б. М. Левитана [1]. Она
подробно изложена в монографиях [2,3] и обзорной статье
[4].![]() и
и![]() в классе q О
L2(0,p) даны в более явной форме. В этой
статье, развивая метод Гельфанда - Левитана, обобщаются результаты [5,6] для
более естественного класса q О L1(0,p).
в классе q О
L2(0,p) даны в более явной форме. В этой
статье, развивая метод Гельфанда - Левитана, обобщаются результаты [5,6] для
более естественного класса q О L1(0,p).![]() = {q,h,h} - четная. Если
= {q,h,h} - четная. Если
![]() - четная, то очевидно, что вместе с
j(x,ln) собственной
функцией задачи (1)-(3) будет также j(p-x,ln). Отсюда, применяя теорему Штурма о нулях j(x,ln), получаем, что
j(p-x,ln) = (-1)nj(x,ln). При x = 0 имеем
- четная, то очевидно, что вместе с
j(x,ln) собственной
функцией задачи (1)-(3) будет также j(p-x,ln). Отсюда, применяя теорему Штурма о нулях j(x,ln), получаем, что
j(p-x,ln) = (-1)nj(x,ln). При x = 0 имеем ![]() (l) однозначно определяются последовательностью
(l) однозначно определяются последовательностью
![]() . Из (17) следует
. Из (17) следует![]() - последовательность собственных значений задачи (1)
- (3) при некотором q0 О
Lp(0,p), h0 и H0, то
существуют четная функция q О Lp(0,p) и число h такие, что ln = ln(q,h,h).
- последовательность собственных значений задачи (1)
- (3) при некотором q0 О
Lp(0,p), h0 и H0, то
существуют четная функция q О Lp(0,p) и число h такие, что ln = ln(q,h,h).![]() ={q,h,h} - искомая тройка, то из (15) и
(17) следует, что
={q,h,h} - искомая тройка, то из (15) и
(17) следует, что
![]() = (-1)n
= (-1)n![]() (ln). Следовательно, rn = (-1)n
(ln). Следовательно, rn = (-1)n![]() j0(p,ln).
j0(p,ln).![]() О L1(0,p), q - четная функция, то из
О L1(0,p), q - четная функция, то из ![]() (x) почти всюду в [0,p].
(x) почти всюду в [0,p].![]() удовлeтворяет условию (6), то существует такое число
h (оно определяется формулой (18)), что из ln(r,h,h) = ln,
(n = 0,1,2,...) функция r О L1(0,p) определяется единственным образом. Эта функция оказывается
четной.
удовлeтворяет условию (6), то существует такое число
h (оно определяется формулой (18)), что из ln(r,h,h) = ln,
(n = 0,1,2,...) функция r О L1(0,p) определяется единственным образом. Эта функция оказывается
четной.![]() = rn
(n = 0,1,2,...) и из условия теоремы 4 и теоремы Марченко о единственности
получаем, что
= rn
(n = 0,1,2,...) и из условия теоремы 4 и теоремы Марченко о единственности
получаем, что
![]() (x) = q(x) почти всюду.
(x) = q(x) почти всюду. ![]() - последовательность собственных значений задачи
(1)-(3), где q - четная и q О Lp(0,p). Тогда j(p - x,ln) = (-1)nj(x,ln). Отсюда следует,
что j([(p)/2],l2n+1) = 0 и jў([(p)/2],l2n) = 0. Это означает, что
- последовательность собственных значений задачи
(1)-(3), где q - четная и q О Lp(0,p). Тогда j(p - x,ln) = (-1)nj(x,ln). Отсюда следует,
что j([(p)/2],l2n+1) = 0 и jў([(p)/2],l2n) = 0. Это означает, что
![]() и
и
![]() являются, соответственно, собственными значениями
краевых задач (1), (2), (21) и (1), (2), (22). Отсюда с помощью следствия 1 и
теоремы 3 можно доказать следующее утверждение.
являются, соответственно, собственными значениями
краевых задач (1), (2), (21) и (1), (2), (22). Отсюда с помощью следствия 1 и
теоремы 3 можно доказать следующее утверждение.![]() и
и
![]() перемежаются:
перемежаются: ![]() и
и
![]() совпадают с собственными значениями задач (1), (2),
(3) с H = 0 и (1), (2), (9), соответственно.
совпадают с собственными значениями задач (1), (2),
(3) с H = 0 и (1), (2), (9), соответственно.![]() была последовательностью собственных значений
некоторой краевой задачи (1), (2), (9), необходимо и достаточно выполнение
асимптотического соотношения (10) при некотором c1.
была последовательностью собственных значений
некоторой краевой задачи (1), (2), (9), необходимо и достаточно выполнение
асимптотического соотношения (10) при некотором c1.