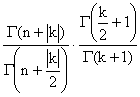МАТЕМАТИКА
УДК 517.53
С. В. Мадоян
Некоторые свойства функций из F-алгебр Зигмунда в шаре и
полидиске
(Представлено чл.-кор. HAH PA Г. Г. Гeвоpкяном 15/ХII
2004)
Пусть n - натуральное и
Cn = {z = (z1,...,zn) : zk О C, 1 Ј k Ј n}. Обозначим G = Bn = {z О
Cn : |z1|2 + ... + |zn|2 < 1}
или G = Un = {z О Cn : |zk| < 1, 1 Ј k Ј n} и, соответственно этим двум
случаям, G = Sn = {z О Cn; |z1|2 + ... + |zn|2 = 1} или
G = Tn = {z О C :
|zk| = 1, 1 Ј k Ј n}. На G существует естественная нормированная инвариантная
относительно вращений G мера s, совпадающая с обычной нормированной мерой Лебега
(площадью) на сфере Sn в случае G =
Sn и являющаяся прямым произведением мер Лебега на единичных
окружностях, составляющих тор Tn, в случае G
= Tn. Символом |z|
для z О C в случае G = Bn будем обознaчать
обычную евклидову норму вектора z, а в случае G = Un под |z| будем понимать поликруговую
норму |z| =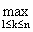 |zk|, z О C. В случае, когда n = 1, шар Bn и поликруг
Un совпадaют с единичным кругом в комплексной плоскости C, сфера
Sn и тор Tn совпадают с единичной окружностью, мера s - с нормированным элементом длины на
ней.
|zk|, z О C. В случае, когда n = 1, шар Bn и поликруг
Un совпадaют с единичным кругом в комплексной плоскости C, сфера
Sn и тор Tn совпадают с единичной окружностью, мера s - с нормированным элементом длины на
ней.
Голоморфную в G функцию f относят к
классу j(N), j - неубывающая
неотрицательная функция вещественного аргумента на положительной полуоси, если
|
sup
0 Ј r Ј 1
|
|
у
х
r
|
j(log+|f(rz)|)s(dz) < +Ґ, | |
где
log+a совпадает с loga, когда a > 1 и log+a = 0 для 0
Ј a < 1. При j(t) = t
получаем класс Неванлинны N в шаре и поликруге, при j(t) = ept, p > 0 - классы Харди Hp.
Пoлагая j(t) = t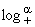 t, a > 0,
приходим к многомерным классам NlogaN,
введенным в случае поликруга Зигмундом в [1, гл. XVII] (под обозначением
Ha) и изучавшимся в обоих случаях в [2]
(a = 1) и в [3] (a і 1), где, в частности, показано, что NlogaN при a і 1 образуют F-алгебры относительно естественных
метрик.
t, a > 0,
приходим к многомерным классам NlogaN,
введенным в случае поликруга Зигмундом в [1, гл. XVII] (под обозначением
Ha) и изучавшимся в обоих случаях в [2]
(a = 1) и в [3] (a і 1), где, в частности, показано, что NlogaN при a і 1 образуют F-алгебры относительно естественных
метрик.
По определению, голоморфная функция f
в области G принадлежит классу j(M), если
|
у
х
G
|
log+ |
0 Ј r Ј
1
|
|f(rz)|s(dz) < +Ґ. | |
При j(t) = t класс j(M) = M в случае шара введен Кимом, Паком и Чоу (см. [4],
[5]); полагая в этом определении j(t) = t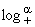 t, a > 0,
получаем многомерные классы MlogaM.
t, a > 0,
получаем многомерные классы MlogaM.
Известно, что
функция f принадлежит классу NlogaN, a > 1, тогда и только тогда, когда f О M и log+|f*| О LlogaL, где
f*(z) =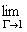 f(rz) - радиальные граничные пределы функции f на G (случай a = 1 рассмотрен в [2],
f(rz) - радиальные граничные пределы функции f на G (случай a = 1 рассмотрен в [2],
случай a > 1 в [3]). Последнее утверждение уточняет
следующая
Теорема 1. Функция f принадлежит NlogaN, a > 1, тогда и только тогда, когда f О Mloga-1M и log+|f*| О LlogaL.
С учетом
вложения M Й Mloga-1M, a > 1, и отмеченного
выше результата [3] понятно, что нетривиальнaя часть уточнения содержит
необходимость теоремы.
Хорошо известно, что
многие топологические свойства F-алгебр голоморфных функций (например,
представление линейных функционалов) устанавливаются через тейлоровские
коэффициенты функций. Верна следующая теоремa.
Теорема 2.
Если f О
Nloga-1N, a > 1, то для коэффициентов Тейлора ak
кратного
ряда Тейлора функции f,
| f(z) = |
е
k О Z+n
|
akzk, z
О G, | |
(1) |
cправедлива
оценка
| ak = Cn,kexp |
й
к
л |
0 |
ж
з
и |
|
|k|n
loga|k|
|
|
ц
ч
ш |
[1/(n+1)]
|
|
щ
ъ
ы |
при |k| ® Ґ, | |
(2) |
в которой
Cn,k =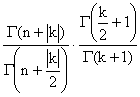 , если G = Bn, и Gn,k = 1, если G = Un, , если G = Bn, и Gn,k = 1, если G = Un, | |
| G |
ж
з
и |
|
k
2
|
+1 |
ц
ч
ш |
= G |
ж
з
и |
|
k1
2
|
+1 |
ц
ч
ш |
...G |
ж
з
и |
|
kn
2
|
+1 |
ц
ч
ш |
, |k| = k1 + ... + kn для k О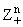 и и | |
| G(s), s >
0 - гамма-функция
Эйлера. | |
Замечание. В случае поликруга G = Un
оценка (2) может быть доказана в следующей, более точной форме:
| |al| Ј exp |
й
к
л |
0 |
ж
з
и |
|
[l]
loga[l]
|
|
ц
ч
ш |
[1/(n+1)]
|
|
щ
ъ
ы |
при |l| ® +Ґ, | |
(2ў) |
где [l]
обозначает произведение всех тех lk,
l = (l1,...,ln), которые отличны от нуля.
Гocyдapcтвeнный инженеpный yнивepcитет
Apмении
Литература
1. Зигмунд А. - Тригонометрические ряды. Т. 2. М. Мир. 1965.
2. Гаврилов В. И., Субботин А. В. - Матер. конф. "Вопр.
функц. анализa и матем. физики." Баку. Чашиоглу. 1999. C.
240-251.
3.
4. Kim H. O., Park Y. Y. - Tsukuba J. Math. 1992. V. 16. N 1. P. 11-18.
5. Choe B. R., Kim H. O. - Complex Variables. 1992. V.
20. P. 53-56.
![]() t, a > 0,
приходим к многомерным классам NlogaN,
введенным в случае поликруга Зигмундом в [1, гл. XVII] (под обозначением
Ha) и изучавшимся в обоих случаях в [2]
(a = 1) и в [3] (a і 1), где, в частности, показано, что NlogaN при a і 1 образуют F-алгебры относительно естественных
метрик.
t, a > 0,
приходим к многомерным классам NlogaN,
введенным в случае поликруга Зигмундом в [1, гл. XVII] (под обозначением
Ha) и изучавшимся в обоих случаях в [2]
(a = 1) и в [3] (a і 1), где, в частности, показано, что NlogaN при a і 1 образуют F-алгебры относительно естественных
метрик.![]() t, a > 0,
получаем многомерные классы MlogaM.
t, a > 0,
получаем многомерные классы MlogaM.![]() f(rz) - радиальные граничные пределы функции f на G (случай a = 1 рассмотрен в [2],
f(rz) - радиальные граничные пределы функции f на G (случай a = 1 рассмотрен в [2],