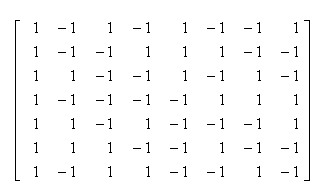УДК 515.164.322

   Классическая теорема Гурвица - Радона утверждает, что на нечетномерной единичной сфере Sⁿ евклидова пространства Rⁿ⁺¹ существует r(n) касательных ортонормальных векторных полей, где r(n) - число Гурвица - Радона. Напомним, что r(n) = 2^r + 8q - 1, где n + 1 = 2^p(2t + 1), p = 4q + r, 3 і r і 0.
   В известных автору доказательствах этой теоремы задача построения касательных полей сводится к алгебраической задаче о существовании некоторой последовательности ортогональных матриц [1,2] либо исследованию возможности наделения пространства Rⁿ⁺¹ структурой C_k - модуля [3].
   В данном сообщении предлагается другое доказательство, основанное на прямом построении вышеупомянутых полей.
   Как известно, сфера S⁷ параллелизуeмa и полную систему ортонормальных касательных полей v₁⁷,v₂⁷,...v₇⁷ можно строить например, формулами:

если  x = (x0,x1,x2,x3,x4,x5,x6) О S7,  то

v17(x) = (x1,-x0,x3,-x2,x5,-x4,-x7,x6),

v27(x) = (x2,-x3,-x0,x1,x6,x7,-x4,-x5),

v37(x) = (x3,x2,-x1,-x0,x7,-x6,x5,-x4),

v47(x) = (x4,-x5,-x6,-x7,-x0,x1,x2,x3),

v57(x) = (x5,x4,-x7,x6,-x1,-x0,-x3,x2),

v67(x) = (x6,x7,x4,-x5,-x2,x3,-x0,-x1),

v77(x) = (x7,-x6,x5,x4,-x3,-x2,x1,-x0).

   Заметим, что каждое поле v_i⁷ определяется некоторой перестановкой индексов координат x₀,x₁,...,x₇ и расстановкой знаков ± перед координатами.
   В работе для всякой нечетномерной сферы будет построена аналогичная полная система ортонормальных полей.
   Пусть n - нечетное число. Рассмотрим некоторую такую подстановку P чисел 0,1,...,n, что p² - тождественная подстановка и P(a) № a для всех a.
   Пусть S - некоторая такая функция на множестве чисел 0,1,...,n, что для всех a

(A)     S(a) = ±1,    S(a) + S(P(a)) = 0.

   Такую пару (P;S) будем называть подходящей парой.
   Исходя из подходящей пары (P;S) определим единичное векторное поле vⁿ : Sⁿ ® Sⁿ на сфере Sⁿ: если x = (x₀,x₁,...,x_n), то vⁿ(x) = (S(0)x_p(0),S(1)x_p(1),...,S(n)x_p(n)).
   Пусть теперь (P₁;S₁), (P₂;S₂), ...,(P_N;S_N) такая последовательность подходящих пар, что

(B)     Pk1 o Pk2 = Pk2 o Pk1  для любых  k1, k2   (o - произведение подстановок);

(C)     Sk1(a) · Sk2(a) + Sk1(Pk2(a)) · Sk2(Pk1(a)) = 0

для любых  k1, k2, k1 № k,  a = 0,1,...,n.

   Рассмотрим соответствующие этим парам векторные поля v₁ⁿ,v₂ⁿ,...,v_Nⁿ.
   Предложение 1. Для любой точки x О Sⁿ векторы x,v₁ⁿ(x),v₂ⁿ(x),...,v_Nⁿ(x) попарно взаимно ортогональны.
   Из предложения 1 следует, что для доказательства теоремы Гурвица - Радона достаточно для всякого нечетного n построить последовательность подходящих пар в количестве P(n), удовлетворяющих условиям (B) и (C).
   Далее определяем подстановки P_k и функции S_k. Сперва для всякого k і 1 будем определять их на множестве всех целых неотрицательных чисел Z₀.
   Представим число a О Z₀ в двоичной системе счисления:

a = е i  (a)i · 2i,   где  (a)i = 0   или   1.

   Для любых чисел a,b О Z₀ определим число a * b формулами

1 * 0 = 0 * 1 = 1,      0 * 0 = 1 * 1 = 0,

a * b= е i  ((a)i * (b)i) · 2i.

   Пусть k = 8m + l і 1, где 7 і l і 0. Определим отображение P_k: Z₀ ® Z₀ формулами:

если  m = 0,   то Pk(a) = l * a;

если  m > 0,   то Pk(a) = 24m-1(2l + 1) * a.

   Отметим, что значения P_k(a) в случае 7 і k і 1, 7 і a і 0 совпадают с нижним индексом a-той координаты вектора v_k⁷(x).
   Предложение 2. P_k - биективное отображение множества Z₀, P_k(a) № a для любого a и P_k² - тождественное отображение множества Z₀. Кроме того, P_k1 o P_k2 = P_k2 o P_k1 для любых k₁, k₂.
   Предложение 3. Для нечетного n ограничение отображения P_k на множество чисел 0,1,...,n является подстановкой этого множества тогда и только тогда, когда r(n) і k і 1.
   Теперь определим функции S_k. Составим матрицу S размерами 7×8

в которой элемент S_k(l), стоящий на пересечении k-той строки (k і l і 1) с l-тым столбцом (7 і l і 0) определяется как знак ±1, стоящий перед l-той координатой вектора v_k⁷(x).
   Наша цель - доопределить значения S_k(l) для всех k і 1 и l і 0.
   Для всякого a і 0 и m і 0 определим числа a^[m] и T_m(a) формулами

a[m] = (a)4m + 2(a)4m+1 + 4 · (a)4m+2;

Tm(a) =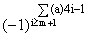

   Ясно, что 7 і a^[m] і 0, T_m(a) = ±1.
   Для произвольного k = 8m + l і 1, где m і 0, 7 і l і 0, и для любого a і 0 определим значение S_k(a) формулами

Sk(a) = Tm-1(a),   если   l = 0, m > 0;

Sk(a) = Tm(a) · Sl(a[m]),   если   l > 0.

   Отметим, что при m = 0, 7 і a і 0 эти формулы - тавтологические тождества.
   Теперь, когда функции S_k полностью определены, составим счетную последовательность пар (P₁,S₁), (P₂,S₂),... .
   Предложение 4. Для каждой пары (P_k,S_k) и для любого a О Z₀ выполняется равенство (А). Для каждых различных k₁,k₂ и для любого a О Z₀ выполняется равенство (C).
   Теперь сформулируем основной результат данной статьи, который непосредственно следует из предложений 1-4.
   Теорема. Пусть n - произвольное нечетное число, r(n) - число Гурвица - Радона. Последовательность отображений v₁ⁿ,v₂ⁿ,...,v_r(n)ⁿ, Sⁿ ® Sⁿ, где

vkn(x) = (Sk(0)xrk(0), Sk(1)xrk(1), ..., Sk(n)xrk(n)),    x = (x0,x1,...,xn) О Sn,

a P_i и S_i - определенные выше подстановки и функции, задает r(n) ортонормальных касательных векторных полей на единичной сфере Sⁿ.
   Поскольку построенные векторные поля v_kⁿ обладают свойством v_kⁿ(-x) = -v_kⁿ(x), то поля v₁ⁿ,v₂ⁿ,...,vⁿ_r(n) определяют ортогональные векторные поля на вещественном проективном пространстве R Pⁿ.

   Ереванский государственный университет

Литература

    1. Radon J. - Abh. Math. Sem. Hamburg. 1922. N1. P. 1-14.
    2. Eckmann B. - Comm. Math. Helv. 1942/3. V. 15. N4. P. 358-366.
    3. Хьюзмоллер Д. М. - Paccлоeниe npocтpaнcтвa. Мир. 1970. 442 c.

---