ФИЗИКА
УДК 531.19
Г. С. Бабаджанян1, С. А. Бабаджанян2
Конденсация Бозе - Эйнштейна в D-мерной системе идеального
газа
бозонов со спектром возбуждения ep = cps в присутствии внешнего поля с
произвольной формой удерживающего потенциала
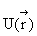
(Представлено академиком Д. М. Седракяном 22/IX 2004)
Введение. Эксперименты
по конденсации Бозе - Эйнштейна (БЭК) побудили к теоретическим исследованиям
термодинамики идеального Бозе-газа, находящегося во внешнем удерживающем поле,
потенциалами которого являются степенные функции. При этом в случае анизотропных
и изотропных полей в целях общности соответствующие степенные потенциалы
представлялись в виде
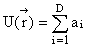 |xi|qi и
|xi|qi и
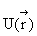 = arq. В тех
же целях потенциалы аксиально-симметричных полей представляем в виде
= arq. В тех
же целях потенциалы аксиально-симметричных полей представляем в виде
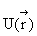 = a^r^q^ + a3|x3|q3. В выражениях для потенциалов
D = 1,2,3 - пространственная размерность системы бозонов, r = (
= a^r^q^ + a3|x3|q3. В выражениях для потенциалов
D = 1,2,3 - пространственная размерность системы бозонов, r = (
 )1/2,
r^ = (x12 + x22)1/2,
где x1,ј,xD О W и W -
объем D-мерной области пространства, занимаемой системой (см. [1, 2]).
)1/2,
r^ = (x12 + x22)1/2,
где x1,ј,xD О W и W -
объем D-мерной области пространства, занимаемой системой (см. [1, 2]).
Результаты исследований показывают, что
внешние поля могут способствовать возникновению БЭК, т.е. тому, чтоб температура
БЭК T0 > 0 [2, 3], и влиять на свойство непрерывности
термодинамических функций в точке T0, тем самым меняя характер
фазового перехода при БЭК [1, 2]. В то же время в отношении указанных аспектов
явления БЭК они не полны и не всегда имеют общий характер; не установлен также
весь спектр возможных характеров ее фазового перехода. Кроме того, с точки
зрения физики фазовых переходов представляется важным в структуре внешних
удерживающих полей провести четкую идентификацию универсального для всех
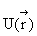 источника и характеристик его влияния на возможность БЭК и характер
ее фазового перехода [4].
источника и характеристик его влияния на возможность БЭК и характер
ее фазового перехода [4].
В настоящей работе в рамках
квазиклассического приближения асимптотическими методами исследуются возможность
БЭК и характер ее фазового перехода (ФП) в идеальном Бозе-газе, находящемся во
внешнем поле с произвольным потенциалом
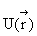 , только лишь удовлетворяющим
общим необходимым требованиям удержания бозонов в (1,2,3)D-мерной области
пространства W. При этом, не исключив возможности
наблюдения явления БЭК в системах бозонов с отличным от ep = p2/2m спектром возбуждения, ep(p) будем задавать в несколько более общем виде,
ep = cps (c,s > 0), например
экситонов [5].
, только лишь удовлетворяющим
общим необходимым требованиям удержания бозонов в (1,2,3)D-мерной области
пространства W. При этом, не исключив возможности
наблюдения явления БЭК в системах бозонов с отличным от ep = p2/2m спектром возбуждения, ep(p) будем задавать в несколько более общем виде,
ep = cps (c,s > 0), например
экситонов [5].
Возможность БЭК и ее
критические параметры. Пусть поле
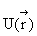 для простоты во всей области
W непрерывно. Кроме того, во всей области W поле
для простоты во всей области
W непрерывно. Кроме того, во всей области W поле
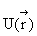 і 0 и на границе
области W имеем U(x1,ј,xD) = Ґ. И пусть в
некоторой точке (x1,ј,xD) О W (для простоты
x1,0 = 0,ј,xD,0 = 0) поле принимает
свое наименьшее значение (
і 0 и на границе
области W имеем U(x1,ј,xD) = Ґ. И пусть в
некоторой точке (x1,ј,xD) О W (для простоты
x1,0 = 0,ј,xD,0 = 0) поле принимает
свое наименьшее значение (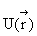 = 0) и эта точка является точкой минимума.
Вместе с тем в окрестности точки минимума асимптотическое поведение поля
аппроксимируется степенными калибровочными функциями, соответственно образующими
либо анизотропную, либо изотропную, либо аксиально-симметричную форму:
= 0) и эта точка является точкой минимума.
Вместе с тем в окрестности точки минимума асимптотическое поведение поля
аппроксимируется степенными калибровочными функциями, соответственно образующими
либо анизотропную, либо изотропную, либо аксиально-симметричную форму:
| U(x1,ј,xD) » |
D
е
i=1
|
ai|xi|qi,
U( |
®
r
|
) »
arq, U( |
®
r
|
) » a^r^q^ + a3|x3|q3. | |
(1) |
Отметим, что большинство реализуемых
полей удовлетворяет такому определению. Тогда для химического потенциала m и полной энергии E системы будем иметь:
N =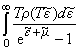 + Ne =
0(T), + Ne =
0(T), |
|
(2) |
E =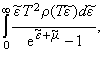
|
|
(3) |
где Ne
= 0(T) - число бозонов на уровне e = 0,
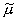 = -m/T,
= -m/T,
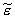 = e/T и e полная энергия частицы
= e/T и e полная энергия частицы
e =
cps +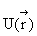 , , |
| |
(4) |
а r( T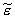 ) - плотность
одночастичных состояний
) - плотность
одночастичных состояний
Температура конденсации
T0 определяется из (2) при m = 0 и
Ne = 0 = 0
Поскольку конечность (бесконечность) значения
интеграла из (6) в конечном счете сводится к его сходимости (несходимости) на
нижнем пределе интегрирования
 ®0), а при
®0), а при
 ®0 область интегрирования
®0 область интегрирования
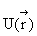 Ј
Ј
 T интеграла из (5)
стягивается в малую окрестность точки минимума
T интеграла из (5)
стягивается в малую окрестность точки минимума
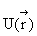 , то влияние внешнего
поля на возможность БЭК, т.е. при T0 > 0, полностью определяется
характером асимптотического поведения поля в окрестности точки его минимума.
Тогда, представив (6) в виде
, то влияние внешнего
поля на возможность БЭК, т.е. при T0 > 0, полностью определяется
характером асимптотического поведения поля в окрестности точки его минимума.
Тогда, представив (6) в виде
| N = |
Ґ
у
х
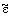 0 0
|
|
T0r(T0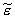 )d )d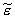
|
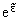 -1 -1
|
+ |
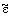 0 0
у
х
0
|
T0r(T0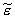 )d )d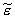
|
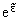 -1 -1
|
|
| |
(7) |
и взяв
 0 настолько малым, чтобы область
интегрирования в (5), т.е. при
0 настолько малым, чтобы область
интегрирования в (5), т.е. при
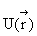 Ј
Ј
 T, охватывала из W только
лишь некоторую окрестность точки абсолютного минимума
T, охватывала из W только
лишь некоторую окрестность точки абсолютного минимума
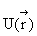 и чтобы в этой
окрестности имело место (1), во втором интеграле (13) для плотности числа
состояний будем иметь
и чтобы в этой
окрестности имело место (1), во втором интеграле (13) для плотности числа
состояний будем иметь
r(T0 ) »
AT0[D/s]+c f -1 ) »
AT0[D/s]+c f -1 |
[D/s]+c f -1
|
|
у
х
[(x1,ј,xD і 0),
(x1+ј+xD Ј 1)]
|
|
ж
и |
1- |
D
е
i=1
|
xi |
ц
ш |
[D/s]-1
|
|
D
Х
i=1
|
xi[1/(qi)]-1dx1јdxD, | |
(8) |
где xi = (ai/ T)|xiqi|, коэффициент A равен A = Ds-1(2p1/2h-1c-1/s)DG-1(1+D/2)
T)|xiqi|, коэффициент A равен A = Ds-1(2p1/2h-1c-1/s)DG-1(1+D/2)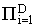 qi-1ai-1/qi, cf - полевой параметр, отражающий характер
асимптотического поведения поля в окрестности точки его минимума, равный
qi-1ai-1/qi, cf - полевой параметр, отражающий характер
асимптотического поведения поля в окрестности точки его минимума, равный
После подстановки (8) во второй
интеграл из (7) и с учетом того, что при
 << 1 имеет место оценка (
<< 1 имеет место оценка ( -1) »
-1) »
 и что ввиду D/s-1 > -1 интеграл из (8) конечен,
правая часть (7) будет конечной и вместе с этим БЭК будет возможной
(T0 > 0) при условии
и что ввиду D/s-1 > -1 интеграл из (8) конечен,
правая часть (7) будет конечной и вместе с этим БЭК будет возможной
(T0 > 0) при условии
где cs = D/s - параметр спектра возбуждения, а c интегральный параметр спектра-поля. Нетрудно показать, что
в случае изотропной и аксиально-симметричной форм асимптотического поведения
внешних полей в условии (10) cf = D/q и cf = 2/q^ + 1/q3 соответственно. При s = 2 условие (10)
совпадает с условием возможности БЭК, полученным в работе [3] для степенного
поля
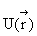 = arq. Кроме того при отсутствии внешнего поля, т.е.
при cf = 0 (q1,ј,qD, q, q^ = Ґ), (10) переходит в обычное
условие возможности БЭК, 0 < s < D (см. например [5]).
= arq. Кроме того при отсутствии внешнего поля, т.е.
при cf = 0 (q1,ј,qD, q, q^ = Ґ), (10) переходит в обычное
условие возможности БЭК, 0 < s < D (см. например [5]).
Характер фазового перехода при
БЭК. Таким образом, при c = cs + cf > 1
имеем T0 > 0, и тогда из m(T0 + 0) = 0 и m(T0 - 0) = 0 следует, что
m(T0 + 0) = = m(T0 - 0) и
E(T0 + 0) = E(T0 - 0), так что в точке
фазового перехода T = T0 термодинамические потенциалы m(T) и E(T) будут непрерывны. Откуда, поскольку W = const и при этом dS = dE/T, энтропия S(T) = E/T + тEdT/T2 также непрерывна и в идеальном газе
бозонов при любом ep = cps и
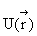 БЭК не может быть ФП1. Обратимся к исследованию поведения k-кратных
производных m и E по T, m(k)(T) и E(k)(T), в точке
T0 (k = 1,2,ј) посредством определения
асимптотических значений (ноль, конечность, бесконечность) скачков БЭК не может быть ФП1. Обратимся к исследованию поведения k-кратных
производных m и E по T, m(k)(T) и E(k)(T), в точке
T0 (k = 1,2,ј) посредством определения
асимптотических значений (ноль, конечность, бесконечность) скачков
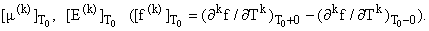 Для этого напишем общие выражения для скачков
начиная с k = 1, которые получаются с учетом того, что N = N(T, Для этого напишем общие выражения для скачков
начиная с k = 1, которые получаются с учетом того, что N = N(T,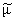 ), E = E(T, ), E = E(T,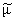 ) и
¶N/¶T = ¶2N/¶T2 =ј = ¶kN/¶Tk є 0 (полное число
бозонов N = ) и
¶N/¶T = ¶2N/¶T2 =ј = ¶kN/¶Tk є 0 (полное число
бозонов N = | const), а также того, что при T Ј
T0 имеем m = ¶m/¶T =ј =
¶km/¶Tk є 0:
|
1
T0
|
|
й
к
л |
¶m
¶T
|
щ
ъ
ы |
T0
|
= |
lim
T®T0+0
|
|
1
T
|
|
ж
з
и |
¶m
¶T
|
ц
ч
ш |
T
|
= |
lim
T®T0+0
|
|
ж
и |
|
Ґ
у
х
0
|
QTd |
ц
ш |
|
ж
и |
|
Ґ
у
х
0
|
Q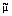 d d |
ц
ш |
-1
|
, | |
(11) |
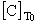 = -
= - |
lim
T®T0+0
|
|
1
T
|
|
¶m
¶T
|
|
Ґ
у
х
0
|
R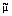 (T, (T,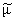 , , )d )d , , |
|
(12) |
|
й
к
л |
¶2E
¶T2
|
щ
ъ
ы |
T0
|
= |
lim
T®T0+0
|
|
м
н
о |
- |
2
T
|
|
¶m
¶T
|
|
Ґ
у
х
0
|
|
ж
з
и |
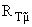 - - |
R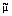
T
|
ц
ч
ш |
d |
+ |
1
T2
|
|
ж
з
и |
¶m
¶T
|
ц
ч
ш |
2
|
|
Ґ
у
х
0
|
R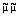 d d |
- |
1
T
|
|
¶2m
¶T2
|
|
Ґ
у
х
0
|
R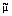 d d |
ь
э
ю |
, | |
(13) |
|
1
T0
|
|
й
к
л |
¶2E
¶T2
|
щ
ъ
ы |
T0
|
= |
lim
T®T0+0
|
|
ж
з
и |
Ґ
у
х
0
|
QTTd |
- |
2
T
|
|
¶m
¶T
|
|
Ґ
у
х
0
|
|
ж
з
и |
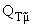 - - |
Q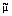
T
|
ц
ч
ш |
d |
+ |
1
T2
|
|
ж
з
и |
¶m
¶T
|
ц
ч
ш |
2
|
|
Ґ
у
х
0
|
Q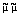 d d |
ц
ч
ш |
|
ж
и |
|
Ґ
у
х
0
|
Q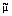 d d |
ц
ш |
-1
|
, | |
(14) |
где через Q = Q(T,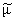 , , и
R = R(T, и
R = R(T,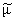 , , ) обозначены подынтегральные выражения из (2) и (3), а QT, Q ) обозначены подынтегральные выражения из (2) и (3), а QT, Q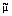 ,ј, RT, R ,ј, RT, R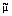 ,ј их частные
производные по T и ,ј их частные
производные по T и
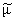 . .
При этом нетрудно заметить, что скачки высших
производных также будут представляться аналогичными (11)-(14) алгебраическими
выражениями относительно несобственных интегралов от производных R и Q по T и
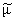 , до k-порядка включительно. Поскольку
асимптотические значения этих скачков (ноль, конечность и бесконечность) также
определяются сходимостью (расходимостью) интегралов из (11)-(14) на нижнем
пределе их интегрирования, в том же числе интегралов из предполагаемых выражений
для скачков высших производных, то влияние внешних полей на характер фазового
перехода при БЭК будет определяться поведением , до k-порядка включительно. Поскольку
асимптотические значения этих скачков (ноль, конечность и бесконечность) также
определяются сходимостью (расходимостью) интегралов из (11)-(14) на нижнем
пределе их интегрирования, в том же числе интегралов из предполагаемых выражений
для скачков высших производных, то влияние внешних полей на характер фазового
перехода при БЭК будет определяться поведением
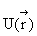 в окрестности точки
его минимума. При этом, учтя, что при e ® 0 имеется оценка (8) и при T ®
T0 имеем m(T) ® 0,
для асимптотических поведений подынтегральных выражений в окрестности точки
его минимума. При этом, учтя, что при e ® 0 имеется оценка (8) и при T ®
T0 имеем m(T) ® 0,
для асимптотических поведений подынтегральных выражений
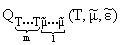 и
и
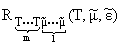 этих интегралов на нижнем пределе интегрирования
e ® 0 будем иметь: этих интегралов на нижнем пределе интегрирования
e ® 0 будем иметь:
|
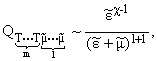 |
(15) |
|
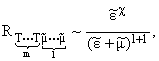 |
(16) |
где m + l = k и k = 1,2,ј порядок дифференцирования m(T) и
E(T) по T. Откуда получаем, что асимптотическое поведение этих интегралов на
нижнем пределе интегрирования аппроксимируется в виде:
|
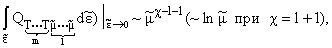 |
(17) |
|
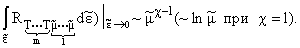 |
(18) |
Подставляя (17) и (18) (с соответствующими
значениями m и l) в выражение для скачков первых производных из (11) и (12),
получаем, что при
БЭК является ФП2 с конечным скачком
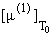 и и
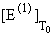 . А при . А при
m(1) и E(1) непрерывны в точке
T = T0, так что при условии (20) БЭК перестает быть ФП2. В то же время
подставляя (17) и (18) в (13) и (14), получаем, что при
m(2) и E(2) при T = T0
перестают быть непрерывными: при 3/2 Ј c Ј 2 скачки
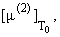 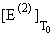 = Ґ и при c = 3/2 конечны. Так что при
условии (21) БЭК является ФП3. А при c < 3/2 m(2) и E(2) непрерывны в точке
T = T0. Поступая аналогичным образом, нетрудно показать, что для k
і 3 скачки = Ґ и при c = 3/2 конечны. Так что при
условии (21) БЭК является ФП3. А при c < 3/2 m(2) и E(2) непрерывны в точке
T = T0. Поступая аналогичным образом, нетрудно показать, что для k
і 3 скачки
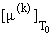 и и
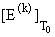 бесконечны при (k+1)/k < c < k/(k-1), бесконечны при (k+1)/k < c < k/(k-1), конечны при c = (k+1)/k и равны нулю при c <
(k+1)/k. Следовательно, при
БЭК согласно классификации
Эренфеста можно считать ФП(n), где n = k+1. При выводе критериев (21) и (22) учитывалось, что
для асимптотических значений скачков
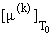 и
и
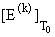 в числителях соответствующих выражений
определяющими являются члены, содержащие в числителях соответствующих выражений
определяющими являются члены, содержащие
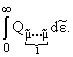
Отметим, что критерии (19) и (21) при s = 2 и
D = 3 переходят в соответствующие критерии, полученные в [1], при этом уточняя
нижнюю границу значения c, при котором БЭК является ФП3
(c = 1 ® c = 3/2). Вместе с этим в отличие от [1] соответственно (22)
имеем, что на области значений c О (1,3/2) БЭК может быть любым ФП(n)
(вплоть до n ® Ґ) с конечным либо бесконечным значением скачков
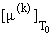 и и
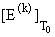 (см. выше). (см. выше).
Универсальная роль критического
параметра спектра-поля для фазовых переходов при БЭК. Таким образом, в
зависимости от D, s и q1,ј,qD
критический параметр c внутри области [0,Ґ) может принимать любые значения (возможные ограничения
могут возникнуть из-за реальных значений D, s). Критерии (10), (19), (21) и (22)
в этой области устанавливают бесконечное число универсальных значений ck = k/(k - 1) (где
k = 1,2,3,ј - кратность производных термодинамических
потенциалов по T) и cҐ =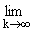 k/(k - 1) = 1, посредством
которых вся область возможных значений c разбивается на
области возможности и невозможности БЭК, т.е. 1 < c < Ґ и 0 < c Ј 1. А уже область возможности БЭК
любыми соседними парами ck и ck+1 разбивается на бесконечное число таких
универсальных интервалов значений Dck - Dc1 є {Ґ > c > 2}, Dc2 є {2 і c
і 3/2}, Dc3 є {3/2 > c і 4/3}, ј, Dck є {k/(k-1) > c і (k+1)/k}, ј, что при c О Dck БЭК может быть только лишь фазовым переходом
порядка n = k+1 с конечными скачками k/(k - 1) = 1, посредством
которых вся область возможных значений c разбивается на
области возможности и невозможности БЭК, т.е. 1 < c < Ґ и 0 < c Ј 1. А уже область возможности БЭК
любыми соседними парами ck и ck+1 разбивается на бесконечное число таких
универсальных интервалов значений Dck - Dc1 є {Ґ > c > 2}, Dc2 є {2 і c
і 3/2}, Dc3 є {3/2 > c і 4/3}, ј, Dck є {k/(k-1) > c і (k+1)/k}, ј, что при c О Dck БЭК может быть только лишь фазовым переходом
порядка n = k+1 с конечными скачками
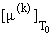 , ,
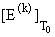 при c =
(k + 1)/k (нижняя граница интервала Dck) и с бесконечным скачком при остальных
значениях c О Dck (за исключением c О Dc1, где БЭК является ФП2 только лишь с конечными
скачками при c =
(k + 1)/k (нижняя граница интервала Dck) и с бесконечным скачком при остальных
значениях c О Dck (за исключением c О Dc1, где БЭК является ФП2 только лишь с конечными
скачками
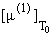 , ,
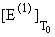 . Откуда заключаем, что критический
параметр c касательно вопросов фазовых переходов при
БЭК во всех отношениях является определяющим. Кроме того, критический параметр
c играет универсальную роль в том смысле, что
бесконечное число различных расширенных систем внешнее поле - система бозонов в
зависимости от пространственной размерности D, степенного показателя спектра
возбуждения ep = cps и характера
асимптотического поведения внешнего удерживающего поля . Откуда заключаем, что критический
параметр c касательно вопросов фазовых переходов при
БЭК во всех отношениях является определяющим. Кроме того, критический параметр
c играет универсальную роль в том смысле, что
бесконечное число различных расширенных систем внешнее поле - система бозонов в
зависимости от пространственной размерности D, степенного показателя спектра
возбуждения ep = cps и характера
асимптотического поведения внешнего удерживающего поля
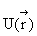 в окрестности
точки его минимума (q1,ј,qD) в
отношении фазовых переходов при БЭК можно разделить на различные классы так,
чтобы внутри каждого класса расширенные системы в критической области имели
идентичное поведение. в окрестности
точки его минимума (q1,ј,qD) в
отношении фазовых переходов при БЭК можно разделить на различные классы так,
чтобы внутри каждого класса расширенные системы в критической области имели
идентичное поведение.
Наконец, поскольку внешние поля с
произвольными удерживающими потенциалами можно разделить на классы идентичности
в отношении значений cf, то поля со
степенными потенциалами при тех же cf в
отношении вопросов фазовых переходов БЭК будут играть роль калибровочных
потенциалов.
В качестве примера рассмотрим систему бозонов
со спектром возбуждения ep = p2/2m.
В случае изотропности формы асимптотического поведения поля в окрестности точки
его минимума, т.е.
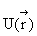 » arn,
параметр c = D/2+D/n и из (10) имеем T0 >
0, если
Причем согласно (19) БЭК является
ФП2 с конечным скачком » arn,
параметр c = D/2+D/n и из (10) имеем T0 >
0, если
Причем согласно (19) БЭК является
ФП2 с конечным скачком
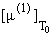 , ,
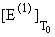 , если , если
И согласно (21) БЭК является ФП3,
если
|
2D
4-D
|
Ј n Ј |
2D
3-D
|
|
м
п
н
п
о
|
|
| |
(25) |
Откуда, в частности, заключаем, что
для D = 3 ни при каком n БЭК не может быть ФП(n > 3).
И наконец, соответственно (18), БЭК является ФП(k + 1) (k і 3), если
|
2(k+1)D
2k-(k-1)D
|
< n Ј |
2kD
2(k+1)-kD
|
|
м
п
н
п
о
|
|
|
| при
2(k-1)/(k+1) < n
Ј
2k/(k+2) | |
|
|
|
|
|
| |
| |
(26) |
1Корпорация Вираж Лоджик
(Virage Logic Corp.)
2Национальный
институт стандартов РА
Литература
1. Bagnato V., Pritchard D. E.,
Kleppner D. - Phys. Rev. A. 1987. V. 35. P.
4354.
2. Dolfavo F., Giorgini S.,
Pitaevskii L., Stringari S. - Review of Modern Physics.
1999. V. 71. P. 463.
3. Salasnich
L., - Math J. Phys. 2000. V. 41. P.
8016.
4. Kadanoff L. P.
- Critical Phenomena. Proc. Int. School Phys. "Enrico Fermi",
Course LJ, Acad. Press New York - London,
1971.
5. Huang K., Statistical Mechanics. John and Sons Inc., New York - London,
1963.
6. Johnson K., Kavaulakis
G. M. - Phys. Rev. Lett. 2001. V. 86. P. 858.
|
![]()
![]()
![]() |xi|qi и
|xi|qi и
![]() = arq. В тех
же целях потенциалы аксиально-симметричных полей представляем в виде
= arq. В тех
же целях потенциалы аксиально-симметричных полей представляем в виде
![]() = a^r^q^ + a3|x3|q3. В выражениях для потенциалов
D = 1,2,3 - пространственная размерность системы бозонов, r = (
= a^r^q^ + a3|x3|q3. В выражениях для потенциалов
D = 1,2,3 - пространственная размерность системы бозонов, r = (
![]() )1/2,
r^ = (x12 + x22)1/2,
где x1,ј,xD О W и W -
объем D-мерной области пространства, занимаемой системой (см. [1, 2]).
)1/2,
r^ = (x12 + x22)1/2,
где x1,ј,xD О W и W -
объем D-мерной области пространства, занимаемой системой (см. [1, 2]). ![]() источника и характеристик его влияния на возможность БЭК и характер
ее фазового перехода [4].
источника и характеристик его влияния на возможность БЭК и характер
ее фазового перехода [4]. ![]() , только лишь удовлетворяющим
общим необходимым требованиям удержания бозонов в (1,2,3)D-мерной области
пространства W. При этом, не исключив возможности
наблюдения явления БЭК в системах бозонов с отличным от ep = p2/2m спектром возбуждения, ep(p) будем задавать в несколько более общем виде,
ep = cps (c,s > 0), например
экситонов [5].
, только лишь удовлетворяющим
общим необходимым требованиям удержания бозонов в (1,2,3)D-мерной области
пространства W. При этом, не исключив возможности
наблюдения явления БЭК в системах бозонов с отличным от ep = p2/2m спектром возбуждения, ep(p) будем задавать в несколько более общем виде,
ep = cps (c,s > 0), например
экситонов [5]. ![]() для простоты во всей области
W непрерывно. Кроме того, во всей области W поле
для простоты во всей области
W непрерывно. Кроме того, во всей области W поле
![]() і 0 и на границе
области W имеем U(x1,ј,xD) = Ґ. И пусть в
некоторой точке (x1,ј,xD) О W (для простоты
x1,0 = 0,ј,xD,0 = 0) поле принимает
свое наименьшее значение (
і 0 и на границе
области W имеем U(x1,ј,xD) = Ґ. И пусть в
некоторой точке (x1,ј,xD) О W (для простоты
x1,0 = 0,ј,xD,0 = 0) поле принимает
свое наименьшее значение (![]() = 0) и эта точка является точкой минимума.
Вместе с тем в окрестности точки минимума асимптотическое поведение поля
аппроксимируется степенными калибровочными функциями, соответственно образующими
либо анизотропную, либо изотропную, либо аксиально-симметричную форму:
= 0) и эта точка является точкой минимума.
Вместе с тем в окрестности точки минимума асимптотическое поведение поля
аппроксимируется степенными калибровочными функциями, соответственно образующими
либо анизотропную, либо изотропную, либо аксиально-симметричную форму:
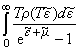 + Ne =
0(T),
+ Ne =
0(T),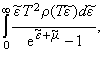
![]() = -m/T,
= -m/T,
![]() = e/T и e полная энергия частицы
= e/T и e полная энергия частицы ![]() ,
, ![]() ) - плотность
одночастичных состояний
) - плотность
одночастичных состояний ![]() )
=
)
=![]()
![]() -
U(
-
U(![]() ))D/s-1dx1јdxD.
))D/s-1dx1јdxD.![]() )d
)d![]()
![]() -1
-1![]() ®0), а при
®0), а при
![]() ®0 область интегрирования
®0 область интегрирования
![]() Ј
Ј
![]() T интеграла из (5)
стягивается в малую окрестность точки минимума
T интеграла из (5)
стягивается в малую окрестность точки минимума
![]() , то влияние внешнего
поля на возможность БЭК, т.е. при T0 > 0, полностью определяется
характером асимптотического поведения поля в окрестности точки его минимума.
Тогда, представив (6) в виде
, то влияние внешнего
поля на возможность БЭК, т.е. при T0 > 0, полностью определяется
характером асимптотического поведения поля в окрестности точки его минимума.
Тогда, представив (6) в виде
![]() 0
0 ![]() )d
)d![]()
![]() -1
-1![]() 0
0![]() )d
)d![]()
![]() -1
-1![]() 0 настолько малым, чтобы область
интегрирования в (5), т.е. при
0 настолько малым, чтобы область
интегрирования в (5), т.е. при
![]() Ј
Ј
![]() T, охватывала из W только
лишь некоторую окрестность точки абсолютного минимума
T, охватывала из W только
лишь некоторую окрестность точки абсолютного минимума
![]() и чтобы в этой
окрестности имело место (1), во втором интеграле (13) для плотности числа
состояний будем иметь
и чтобы в этой
окрестности имело место (1), во втором интеграле (13) для плотности числа
состояний будем иметь
![]() ) »
AT0[D/s]+c f -1
) »
AT0[D/s]+c f -1![]()
![]() T)|xiqi|, коэффициент A равен A = Ds-1(2p1/2h-1c-1/s)DG-1(1+D/2)
T)|xiqi|, коэффициент A равен A = Ds-1(2p1/2h-1c-1/s)DG-1(1+D/2)![]() qi-1ai-1/qi, cf - полевой параметр, отражающий характер
асимптотического поведения поля в окрестности точки его минимума, равный
qi-1ai-1/qi, cf - полевой параметр, отражающий характер
асимптотического поведения поля в окрестности точки его минимума, равный
![]() << 1 имеет место оценка (
<< 1 имеет место оценка (![]() -1) »
-1) »
![]() и что ввиду D/s-1 > -1 интеграл из (8) конечен,
правая часть (7) будет конечной и вместе с этим БЭК будет возможной
(T0 > 0) при условии
и что ввиду D/s-1 > -1 интеграл из (8) конечен,
правая часть (7) будет конечной и вместе с этим БЭК будет возможной
(T0 > 0) при условии
![]() = arq. Кроме того при отсутствии внешнего поля, т.е.
при cf = 0 (q1,ј,qD, q, q^ = Ґ), (10) переходит в обычное
условие возможности БЭК, 0 < s < D (см. например [5]).
= arq. Кроме того при отсутствии внешнего поля, т.е.
при cf = 0 (q1,ј,qD, q, q^ = Ґ), (10) переходит в обычное
условие возможности БЭК, 0 < s < D (см. например [5]). ![]() БЭК не может быть ФП1. Обратимся к исследованию поведения k-кратных
производных m и E по T, m(k)(T) и E(k)(T), в точке
T0 (k = 1,2,ј) посредством определения
асимптотических значений (ноль, конечность, бесконечность) скачков
БЭК не может быть ФП1. Обратимся к исследованию поведения k-кратных
производных m и E по T, m(k)(T) и E(k)(T), в точке
T0 (k = 1,2,ј) посредством определения
асимптотических значений (ноль, конечность, бесконечность) скачков
![]() Для этого напишем общие выражения для скачков
начиная с k = 1, которые получаются с учетом того, что N = N(T,
Для этого напишем общие выражения для скачков
начиная с k = 1, которые получаются с учетом того, что N = N(T,![]() ), E = E(T,
), E = E(T,![]() ) и
¶N/¶T = ¶2N/¶T2 =ј = ¶kN/¶Tk є 0 (полное число
бозонов N =
) и
¶N/¶T = ¶2N/¶T2 =ј = ¶kN/¶Tk є 0 (полное число
бозонов N =![]()
![]() d
d![]()
![]() = -
= -![]() (T,
(T,![]() ,
,![]() )d
)d![]() ,
,![]() -
-![]()
![]()
![]() d
d![]()
![]() d
d![]()
![]()
![]() -
-![]()
![]()
![]() d
d![]()
![]() d
d![]()
![]() ,
,![]() и
R = R(T,
и
R = R(T,![]() ,
,![]() ) обозначены подынтегральные выражения из (2) и (3), а QT, Q
) обозначены подынтегральные выражения из (2) и (3), а QT, Q![]() ,ј, RT, R
,ј, RT, R![]() ,ј их частные
производные по T и
,ј их частные
производные по T и
![]() .
. ![]() , до k-порядка включительно. Поскольку
асимптотические значения этих скачков (ноль, конечность и бесконечность) также
определяются сходимостью (расходимостью) интегралов из (11)-(14) на нижнем
пределе их интегрирования, в том же числе интегралов из предполагаемых выражений
для скачков высших производных, то влияние внешних полей на характер фазового
перехода при БЭК будет определяться поведением
, до k-порядка включительно. Поскольку
асимптотические значения этих скачков (ноль, конечность и бесконечность) также
определяются сходимостью (расходимостью) интегралов из (11)-(14) на нижнем
пределе их интегрирования, в том же числе интегралов из предполагаемых выражений
для скачков высших производных, то влияние внешних полей на характер фазового
перехода при БЭК будет определяться поведением
![]() в окрестности точки
его минимума. При этом, учтя, что при e ® 0 имеется оценка (8) и при T ®
T0 имеем m(T) ® 0,
для асимптотических поведений подынтегральных выражений
в окрестности точки
его минимума. При этом, учтя, что при e ® 0 имеется оценка (8) и при T ®
T0 имеем m(T) ® 0,
для асимптотических поведений подынтегральных выражений
![]() и
и
![]() этих интегралов на нижнем пределе интегрирования
e ® 0 будем иметь:
этих интегралов на нижнем пределе интегрирования
e ® 0 будем иметь: 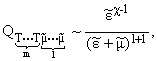
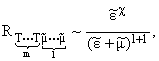
![]()
![]()
![]() и
и
![]() . А при
. А при ![]()
![]() = Ґ и при c = 3/2 конечны. Так что при
условии (21) БЭК является ФП3. А при c < 3/2 m(2) и E(2) непрерывны в точке
T = T0. Поступая аналогичным образом, нетрудно показать, что для k
і 3 скачки
= Ґ и при c = 3/2 конечны. Так что при
условии (21) БЭК является ФП3. А при c < 3/2 m(2) и E(2) непрерывны в точке
T = T0. Поступая аналогичным образом, нетрудно показать, что для k
і 3 скачки
![]() и
и
![]() бесконечны при (k+1)/k < c < k/(k-1),
бесконечны при (k+1)/k < c < k/(k-1), ![]() и
и
![]() в числителях соответствующих выражений
определяющими являются члены, содержащие
в числителях соответствующих выражений
определяющими являются члены, содержащие
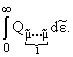
![]() и
и
![]() (см. выше).
(см. выше).
![]() k/(k - 1) = 1, посредством
которых вся область возможных значений c разбивается на
области возможности и невозможности БЭК, т.е. 1 < c < Ґ и 0 < c Ј 1. А уже область возможности БЭК
любыми соседними парами ck и ck+1 разбивается на бесконечное число таких
универсальных интервалов значений Dck - Dc1 є {Ґ > c > 2}, Dc2 є {2 і c
і 3/2}, Dc3 є {3/2 > c і 4/3}, ј, Dck є {k/(k-1) > c і (k+1)/k}, ј, что при c О Dck БЭК может быть только лишь фазовым переходом
порядка n = k+1 с конечными скачками
k/(k - 1) = 1, посредством
которых вся область возможных значений c разбивается на
области возможности и невозможности БЭК, т.е. 1 < c < Ґ и 0 < c Ј 1. А уже область возможности БЭК
любыми соседними парами ck и ck+1 разбивается на бесконечное число таких
универсальных интервалов значений Dck - Dc1 є {Ґ > c > 2}, Dc2 є {2 і c
і 3/2}, Dc3 є {3/2 > c і 4/3}, ј, Dck є {k/(k-1) > c і (k+1)/k}, ј, что при c О Dck БЭК может быть только лишь фазовым переходом
порядка n = k+1 с конечными скачками
![]() ,
,
![]() при c =
(k + 1)/k (нижняя граница интервала Dck) и с бесконечным скачком при остальных
значениях c О Dck (за исключением c О Dc1, где БЭК является ФП2 только лишь с конечными
скачками
при c =
(k + 1)/k (нижняя граница интервала Dck) и с бесконечным скачком при остальных
значениях c О Dck (за исключением c О Dc1, где БЭК является ФП2 только лишь с конечными
скачками
![]() ,
,
![]() . Откуда заключаем, что критический
параметр c касательно вопросов фазовых переходов при
БЭК во всех отношениях является определяющим. Кроме того, критический параметр
c играет универсальную роль в том смысле, что
бесконечное число различных расширенных систем внешнее поле - система бозонов в
зависимости от пространственной размерности D, степенного показателя спектра
возбуждения ep = cps и характера
асимптотического поведения внешнего удерживающего поля
. Откуда заключаем, что критический
параметр c касательно вопросов фазовых переходов при
БЭК во всех отношениях является определяющим. Кроме того, критический параметр
c играет универсальную роль в том смысле, что
бесконечное число различных расширенных систем внешнее поле - система бозонов в
зависимости от пространственной размерности D, степенного показателя спектра
возбуждения ep = cps и характера
асимптотического поведения внешнего удерживающего поля
![]() в окрестности
точки его минимума (q1,ј,qD) в
отношении фазовых переходов при БЭК можно разделить на различные классы так,
чтобы внутри каждого класса расширенные системы в критической области имели
идентичное поведение.
в окрестности
точки его минимума (q1,ј,qD) в
отношении фазовых переходов при БЭК можно разделить на различные классы так,
чтобы внутри каждого класса расширенные системы в критической области имели
идентичное поведение. ![]() » arn,
параметр c = D/2+D/n и из (10) имеем T0 >
0, если
» arn,
параметр c = D/2+D/n и из (10) имеем T0 >
0, если
![]() ,
,
![]() , если
, если