МЕХАНИКА
УДК 539.3
Г. С. Никогосян, С. О. Саркисян
Упругие тонкие оболочки по несимметричной теории упругости
со
стесненным вращением
(Представлено академиком Л.А. Агаловяном 31/I 2005)
В последние десятилетия наряду с классической
теорией упругости интенсивно развиваются математические модели микрополярных
упругих сред с учетом вращательного взаимодействия и моментных напряжений. С
использованием методологии континуума на основе микрополярной (несимметричной,
моментной) теории упругости рассматривается влияние микроструктуры материала тел
на напряженно-деформированное состояние и динамические характеристики; изучаются
эффекты концентрации напряжений вокруг отверстий и трещин, задачи механики
разрушения. Актуальна проблема построения теорий микрополярных упругих тонких
стержней, пластин и оболочек [1]. В [1] с использованием достижений
общеизвестной уточненной теории пластин и оболочек [2,3] по трехмерной
несимметричной теории упругости с независимыми полями перемещений и вращений [4]
на основе метода гипотез построена микрополярная теория пластин и оболочек. На
основе метода гипотез по трехмерной несимметричной теории упругости со
стесненным вращением [4-8] выведены уравнения тонкой цилиндрической оболочки
[9].
Одним из основных методов построения теории
упругих тонких стержней, пластин и оболочек является асимптотический метод
[10-13], весьма эффективный также при построении теории тонких стержней, пластин
и оболочек, когда граничные условия на лицевых поверхностях указанных тел
являются неклассическими (в смысле теории пластин и оболочек) [11,12]. В [14]
разработан асимптотический подход и построена асимптотическая теория
микрополярных упругих тонких пластин, в основе которой лежит трехмерная
несимметричная теория упругости с независимыми полями перемещений и вращений
(НТУ с НППВ). Построена прикладная-двумерная теория микрополярных упругих тонких
пластин на основе НТУ с НППВ. В [15] на основе НТУ с НППВ построены
асимптотическая теория микрополярных упругих тонких оболочек и
прикладная-двумерная теория микрополярных оболочек.
В данной статье развивается асимптотический
подход работ [14,15] и построена асимптотическая теория микрополярных упругих
тонких оболочек на основе несимметричной теории упругости со стесненным
вращением (НТУ с СВ). Построена прикладная-двумерная теория микрополярных
упругих тонких оболочек на основе НТУ с СВ.
1. Будем рассматривать
оболочку постоянной толщины 2h как трехмерное упругое тело. Дифференциальные
уравнения несимметричной теории упругости со стесненным вращением имеют вид
[4-6]:
уравнения равновесия
| Сjsji = 0,
Сjmji + eijk · sjk = 0; | |
(1.1) |
соотношения упругости
|
м
п
н
п
о |
|
1
2
|
(sij + sji) = 2m · gij + l · gkk · dij, | |
| mji = (g + e)kji + (g - e)kij + b ·
kkk · dij; | | |
| |
(1.2) |
геометрические соотношения
|
®
w
|
= |
1
2
|
· |
rot
|
®
u
|
, gji = |
1
2
|
· (Сjui + Сiuj),
kji = Сjwi
(i,j = 1,2,3), | |
(1.3) |
где sij, mij -
соответственно контравариантные компоненты силового и моментного тензоров
напряжений;
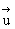 - вектор перемещения;
- вектор перемещения;
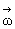 - вектор поворота; gji,
kji
- соответственно ковариантные компоненты тензора деформации и тензора
изгиба-кручения; l, m, b, g, e -
упругие константы материала оболочки.
- вектор поворота; gji,
kji
- соответственно ковариантные компоненты тензора деформации и тензора
изгиба-кручения; l, m, b, g, e -
упругие константы материала оболочки.
Далее отнесем оболочку к триортогональной
системе координат ai(i = 1,2,3), принятой в
теории оболочек [7]. К определяющим уравнениям НТУ с СВ (1.1)-(1.3) присоединим
соответствующие граничные условия. Для граничных условий на лицевых поверхностях
оболочки примем граничные условия первой граничной задачи НТУ с СВ, которые
можем записать:
| s3i = -±qi±, m3i = -±mi± при
a3 = ±h (i = 1,2,3)
| |
(1.4) |
Граничными условиями на боковой
поверхности оболочки (которая представляет собой замкнутый торец) могут быть
граничные условия первой, второй или смешанной граничной задачи НТУ с СВ; для
определенности примем граничные условия первой граничной задачи:
| sjinj = pi*
(i = 1,2,3), mjknj = mk*
(k = 1,2,3) при a1 = a10. | |
(1.5) |
Отметим, что НТУ с СВ имеет некоторые
особенности [5]: а) в этой теории Коссера можно считать инвариант моментного
тензора напряжений m11 + m22 + m33 равным
нулю: m11 + m22 + m33 = 0, что
в свою очередь означает, что упругая константа b входит
в физические соотношения (1.2) формально и не играет никакой роли; б) число как
силовых, так и геометрических граничных условий равно пяти, а не шести, как
формально было представлено формулами (1.4), (1.5)
Перейдем к построению внутреннего
итерационного процесса поставленной краевой задачи НТУ с СВ.
Введем новые независимые переменные, положив
[7]:
| ai = R · l-p · xi, a3 = R · l-l · z
(i = 1,2), | |
(1.6) |
где R - некоторый характерный
радиус кривизны срединной поверхности, p,l - целые числа, удовлетворяющие
неравенствам l > p і 0, а l
- большой постоянный параметр, определяемый формулой h = R · l-l.
В трехмерных уравнениях (1.1)-(1.3) по
формулам работы [15] перейдем к безразмерным величинам
|
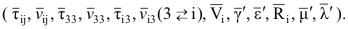 |
Будем считать, что упругие
константы материала оболочки
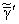 и
и
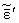 имеют представления
имеют представления
|
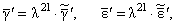 |
(1.7) |
где величины
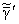 ,
,
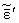 считаются величинами
порядка l0.
считаются величинами
порядка l0.
Тогда из полученной системы уравнений на
уровне асимптотической точности 0(lp-l) часть величин можем получить интегрированием по
переменной z:
|
м
п
п
п
п
п
п
н
п
п
п
п
п
п
о
|
|
|
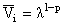 |
ж
и
|
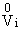 (x1,x2) + l2p-l-cz · (x1,x2) + l2p-l-cz · |
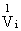 (x1,x2) (x1,x2) |
ц
ш
|
,
|
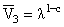 · · |
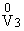 (x1,x2), (x1,x2),
| |
|
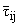 = ll = ll |
ж
и
|
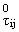 (x1,x2) + l2p-l-cz · (x1,x2) + l2p-l-cz · |
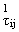 (x1,x2) (x1,x2) |
ц
ш
|
, | |
|
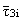 = lp = lp |
ж
и
|
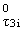 (x1,x2) + z · (x1,x2) + z · |
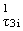 (x1,x2) + l2p-l-cz2 · (x1,x2) + l2p-l-cz2 ·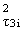 (x1,x2) (x1,x2) |
ц
ш
|
, | |
wi = lp+l-c ·
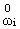 (x1,x2),
w3 = ll (x1,x2),
w3 = ll |
ж
и
|
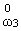 (x1,x2) + l2p-l-cz · (x1,x2) + l2p-l-cz · |
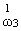 (x1,x2) (x1,x2) |
ц
ш
|
, | |
|
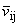 = l2p-l-c ·
= l2p-l-c ·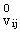 (x1,x2), (x1,x2), |
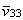 = l2p-l-c · = l2p-l-c · |
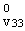 (x1,x2),
(i = 1,2, j = 1,2), (x1,x2),
(i = 1,2, j = 1,2),
| | |
| |
(1.8) |
где c = 0 при 2p Ј l и c = 2p - l при 2p і l;
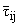 - несимметричный тензор силовых напряжений
[7],
- несимметричный тензор силовых напряжений
[7],
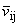 -
аналогичный тензор для моментных напряжений [15].
-
аналогичный тензор для моментных напряжений [15].
Здесь основными функциями, зависящими от
x1 и x2,
являются
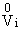 (x1,x2) и (x1,x2) и
|
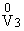 (x1,x2);
остальные величины будут определяться через указанные функции по соответствующим
формулам. Остальная часть расчетных величин поставленной трехмерной задачи
выражается через вышеотмеченные величины и через величины (x1,x2);
остальные величины будут определяться через указанные функции по соответствующим
формулам. Остальная часть расчетных величин поставленной трехмерной задачи
выражается через вышеотмеченные величины и через величины
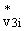 , для определения которых
приходим к дифференциальным уравнениям (относительно координаты z) с соответствующими граничными условиями при z ± 1. , для определения которых
приходим к дифференциальным уравнениям (относительно координаты z) с соответствующими граничными условиями при z ± 1.
Далее переходим к осредненным по толщине
оболочки силовым и моментным характеристикам [14,15] и одновременно к понятиям
перемещений и поворотов точек срединной поверхности оболочки. На основе
построенной асимптотики для поставленной краевой задачи (1.1)-(1.5) на уровне
асимптотической точности 0(lp-l) приходим к следующей разрешающей системе двумерных
уравнений:
уравнения равновесия
|
м
п
п
п
п
п
п
п
п
п
п
п
п
п
п
н
п
п
п
п
п
п
п
п
п
п
п
п
п
о
|
|
1
Ai
|
· |
¶Tii
¶ai
|
+ |
1
AiAj
|
· |
¶Aj
¶ai
|
· (Tii - Tjj) + |
1
Aj
|
· |
¶Sji
¶aj
|
+ | |
| + |
1
AiAj
|
· |
¶Ai
¶aj
|
·(Sij + Sji) - (qi+ + qi-) = 0, | |
|
1
A1
|
· |
¶(G11 - L12)
¶a1
|
+ |
1
A1A2
|
· |
¶A2
¶a1
|
· ((G11 - L12) - (G22 + L21)) - | |
| - |
1
A2
|
· |
¶(H21 + L22)
¶a2
|
- |
1
A1A2
|
· |
¶A1
¶a2
|
· ((H12 - L11) + (H21 + L22)) - | |
| -N13 + [h(q1+ - q1-) + (m2+ + m2-)] = 0, | |
|
1
A2
|
· |
¶(G22 + L21)
¶a2
|
+ |
1
A1A2
|
· |
¶A1
¶a2
|
· ((G22 + L21) - (G11 - L12)) - | |
| - |
1
A1
|
· |
¶(H12 - L11)
¶a1
|
- |
1
A1A2
|
· |
¶A2
¶a1
|
· ((H21 + L22) + (H12 - L11)) - | |
| -N23 + [h(q2+ - q2-) - (m1+ + m1-)] = 0, | |
|
T11
R1
|
+ |
T22
R2
|
+ |
1
A1A2
|
· |
й
к
л
|
¶
¶a1
|
(A2N13) + |
¶
¶a2
|
(A1N23) |
щ
ъ
ы
|
+(q3+ + q3-) = 0; | | |
| |
(1.9) |
соотношения упругости
|
м
п
п
п
н
п
п
п
о
|
| Tii = 2h · |
4m(m + l)
2m + l
|
· |
ж
з
и
|
Gii + |
l
2(m + l)
|
· Gjj |
ц
ч
ш
|
, | |
| Sij = 2mh · |
ж
з
и
|
Gij + Gji |
ц
ч
ш
|
, | |
| Gii = - |
2
3
|
h3 · |
4m(m + l)
2m + l
|
· |
ж
з
и
|
Kii + |
l
2(m + l)
|
· Kjj |
ц
ч
ш
|
, | |
| Hij = |
2
3
|
mh3 · |
ж
з
и
|
Kij + Kji |
ц
ч
ш
|
, | |
| Lij = 2h · |
ж
и
|
(g + e) · cij - (g - e) · cji |
ц
ш
|
, | |
| |
| |
(1.10) |
геометрические соотношения
|
м
п
п
п
п
п
п
п
н
п
п
п
п
п
п
п
о
|
| Gii = |
1
Ai
|
· |
¶ui
¶ai
|
+ |
1
AiAj
|
· |
¶Ai
¶aj
|
· uj - |
w
Ri
|
,
Kii = |
1
Ai
|
· |
¶bi
¶ai
|
+ |
1
AiAj
|
· |
¶Ai
¶aj
|
· bj, | |
| Gij = |
1
Ai
|
· |
¶uj
¶ai
|
- |
1
AiAj
|
· |
¶Ai
¶aj
|
· ui,
Kij = |
1
Ai
|
· |
¶bj
¶ai
|
- |
1
AiAj
|
· |
¶Ai
¶aj
|
· bi, | |
| cii = |
1
Ai
|
· |
¶Wi
¶ai
|
+ |
1
AiAj
|
· |
¶Ai
¶aj
|
· Wj- |
W3
Ri
|
, cij = |
1
Ai
|
· |
¶Wj
¶ai
|
- |
1
AiAj
|
· |
¶Ai
¶aj
|
· Wi, | |
| bi = |
1
Ai
|
· |
¶w
¶ai
|
+ |
ui
Ri
|
,
Wi = (-1)i · bj, | |
| W3 = - |
1
2
|
· |
ж
з
и
|
|
1
A1
|
· |
¶u2
¶a1
|
- |
1
A1A2
|
· |
¶A1
¶a2
|
· u1- |
1
A2
|
· |
¶u1
¶a2
|
+ |
1
A1A2
|
· |
¶A2
¶a1
|
· u2 |
ц
ч
ш
|
. | | |
| |
(1.11) |
Здесь Tii,
S12, S21 - усилия; N13, N23 -
перерезывающие силы; Gii, H12, H21 - моменты
силового происхождения; Lii, L12, L21 - моменты
моментного происхождения; Gii, G12, G21 -
компоненты тензора деформации в точках срединной поверхности оболочки;
Kii, K12, K21 - компоненты тензора изгибных
деформаций и кручения, связанные с моментами силового происхождения; cii, c12,
c21 - компоненты тензора изгибных деформаций
и кручения, связанные с моментами моментного происхождения; ui, w -
перемещения точек срединной поверхности оболочки; Wi, W3 -
компоненты вектора вращения точек срединной поверхности оболочки. После решения
основной разрешающей системы уравнений (1.9)-(1.11) остальные искомые величины
будут определяться по соответствующим формулам. (1.9)-(1.11) представляют собой
уравнения разрешающей системы прикладной-двумерной теории микрополярных упругих
тонких оболочек, когда в ее основу положена трехмерная НТУ с СВ.
2. Обратимся к изучению
краевых упругих явлений; отправными также будут уравнения трехмерной теории НТУ
с СВ (1.1)-(1.3).
Будем считать, что край оболочки, вблизи
которого надо исследовать напряженное состояние, задается уравнением a1 = a10, и
введем замену независимых переменных по формулам [7]:
| a1 - a10 = Rl-l · x1, a2 = Rl-p · x2, a3 = Rl-l · z, | |
(2.1) |
где величины R,l, l,p имеют тот же смысл, что и в (1.6).
В трехмерных уравнениях (1.1)-(1.3) по
формулам работы [15] перейдем к безразмерным величинам и выполним
соответствующие замены искомых величин.
После этого уравнения НТУ с СВ можем
представить в виде двух групп уравнений и при отбрасывании величин порядка lp-l получим две
отдельные группы независимых однородных уравнений, представляющих собой системы
уравнений так называемой смешанной, силовой-моментной (антиплоской и плоской)
погранслойной задачи несимметричной теории упругости. Будем исходить из
предположения, что напряженное состояние трехмерного тела оболочки по НТУ с СВ
составляется из внутреннего напряженного состояния и погранслоев:
(НДС)полн = (НДС)вн + l
r ·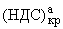 + l
q · + l
q ·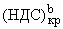 , , | |
(2.2) |
где числа r,q назовем показателями интенсивности плоского и антиплоского
погранслоев, которые пока произвольны. Считается, что погранслои локализуются
вблизи бокового края оболочки.
Для того, чтобы осуществить сращивание
внутренней задачи и погранслоев по НТУ с СВ , следует подставить (2.2) в
граничные условия (1.5). При этом показатели r и q
будем выбирать так, чтобы итерационный процесс для выполнения граничных условий
(1.5) был удобным.
Единственно приемлемые значения r и q в случае нагруженного края оболочки на уровне
асимптотической точности 0(lp-l) определяются так:
С учетом (2.3), в результате подстановки
(2.2) в условия (1.5) и ограничиваясь асимптотической точностью 0(lp-l), получим, что
граничные условия трехмерной теории НТУ с СВ (1.5) расщепляются между внутренней
задачей (прикладной-двумерной теорией оболочек) и погранслойными задачами.
Для прикладной-двумерной теории микрополярных
оболочек (определяющая система уравнений (1.9)-(1.11)) получим граничные условия
следующего вида:
|
м
п
п
п
п
н
п
п
п
п
о
|
| T11 |
к
к
к
|
a1=a10
|
= |
h
у
х
-h
|
p*1da3,
S12 |
к
к
к
|
a1=a10
|
= |
h
у
х
-h
|
p*2da3, | |
|
ж
з
и
|
-N13 + |
1
A2
|
· |
¶
¶a2
|
|
ж
и
|
H12 - L11 |
ц
ш
|
ц
ч
ш
|
|
к
к
к
|
a1=a10
|
= |
h
у
х
-h
|
|
ж
з
и
|
p*3 + |
1
A2
|
· |
¶
¶a2
|
|
ж
и
|
a3 · p*2 - m*1 |
ц
ш
|
ц
ч
ш
|
da3, | |
|
ж
и
|
L12 - G11 |
ц
ш
|
|
к
к
к
|
a1=a10
|
= |
h
у
х
-h
|
|
ж
и
|
m*2 + a3 · p*1 |
ц
ш
|
da3. | | |
| |
(2.4) |
Уравнения (1.9)-(1.11) и граничные условия
(2.4) составляют граничную задачу прикладной-двумерной теории микрополярных
упругих тонких оболочек, когда в ее основу положена трехмерная НТУ с СВ.
Отдельные граничные условия получены также
для погранслойных уравнений.
Гюмрийский государственный
педагогический институт им. М. Налбандяна
Литература
1. Амбарцумян С.А. Микрополярная теория оболочек и пластин. Ереван. Изд-во НАН Армении.
1999. 214 с.
2. Амбарцумян С.А.
Теория анизотропных пластин. М. Наука. 1967. 266 с.
3. Амбарцумян С.А. Общая теория анизотропных оболочек. М. Наука. 1974. 446
с.
4. Новацкий В. Теория упругости. М. Мир. 1975. 862 с.
5. Койтер В. Т. - Механика. Период. сб. перев. иностр. статей. 1965. N3. С. 89-112.
6. Миндлин Р. Д., Тирстен Г. Ф.
- Механика. Период. сб. перев. иностр. статей. 1964. N4. С.
80-114.
7. Савин Г.Н.
Основы плоской моментной теории упругости. Киев. Изд-во
Киевск. ун-та. 1965. 162 с.
8. Морозов. Н.Ф. Избранные двумерные задачи теории
упругости. Л. Изд-во ЛГУ. 1978. 182 с.
9. Бабич Д. В. - ПМ. Т. II. В. 12. 1966. С.
41-48.
10. Гольденвейзер А.Л.
Теория упругих тонких оболочек. М. Наука. 1976. 510
с.
11. Агаловян Л.А. Асимптотическая теория анизотропных пластин и оболочек. М. Наука. 1997.
414 с.
12. Агаловян Л.А.
- ПМ. 2002. Т. 38. N7. C.
3-24.
13. Саркисян С.О.
Общая двумерная теория магнитоупругости тонких оболочек.
Ереван. Изд-во АН Армении. 1992. 260 с.
14. Саркисян С.О. В: Сб. науч. трудов, посвященный
80-летию академика НАН РА С.А. Амбарцумяна. Ереван. Изд-во НАН РА. 2002. С.
285-296.
15. Никогосян Г. С.,
Саркисян С. О. - Изв. НАН Армении. Механика. 2005. Т. 58.
N1.
|
![]() - вектор перемещения;
- вектор перемещения;
![]() - вектор поворота; gji,
kji
- соответственно ковариантные компоненты тензора деформации и тензора
изгиба-кручения; l, m, b, g, e -
упругие константы материала оболочки.
- вектор поворота; gji,
kji
- соответственно ковариантные компоненты тензора деформации и тензора
изгиба-кручения; l, m, b, g, e -
упругие константы материала оболочки. ![]()
![]() и
и
![]() имеют представления
имеют представления
![]()
![]() ,
,
![]() считаются величинами
порядка l0.
считаются величинами
порядка l0. ![]()
![]() (x1,x2) + l2p-l-cz ·
(x1,x2) + l2p-l-cz ·![]() (x1,x2)
(x1,x2)![]() ·
·![]() (x1,x2),
(x1,x2),
![]() = ll
= ll![]() (x1,x2) + l2p-l-cz ·
(x1,x2) + l2p-l-cz ·![]() (x1,x2)
(x1,x2)![]() = lp
= lp![]() (x1,x2) + z ·
(x1,x2) + z ·![]() (x1,x2) + l2p-l-cz2 ·
(x1,x2) + l2p-l-cz2 ·![]() (x1,x2)
(x1,x2)![]() (x1,x2),
w3 = ll
(x1,x2),
w3 = ll![]() (x1,x2) + l2p-l-cz ·
(x1,x2) + l2p-l-cz ·![]() (x1,x2)
(x1,x2)![]() = l2p-l-c ·
= l2p-l-c ·![]() (x1,x2),
(x1,x2),![]() = l2p-l-c ·
= l2p-l-c ·![]() (x1,x2),
(i = 1,2, j = 1,2),
(x1,x2),
(i = 1,2, j = 1,2),
![]() - несимметричный тензор силовых напряжений
[7],
- несимметричный тензор силовых напряжений
[7],
![]() -
аналогичный тензор для моментных напряжений [15].
-
аналогичный тензор для моментных напряжений [15]. ![]() (x1,x2) и
(x1,x2) и
![]() (x1,x2);
остальные величины будут определяться через указанные функции по соответствующим
формулам. Остальная часть расчетных величин поставленной трехмерной задачи
выражается через вышеотмеченные величины и через величины
(x1,x2);
остальные величины будут определяться через указанные функции по соответствующим
формулам. Остальная часть расчетных величин поставленной трехмерной задачи
выражается через вышеотмеченные величины и через величины
![]() , для определения которых
приходим к дифференциальным уравнениям (относительно координаты z) с соответствующими граничными условиями при z ± 1.
, для определения которых
приходим к дифференциальным уравнениям (относительно координаты z) с соответствующими граничными условиями при z ± 1. ![]() + l
q ·
+ l
q ·![]() ,
,