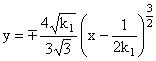МЕХАНИКА
УДК 539.1
Член-корреспондент НАН РА А. Г. Багдоев, Г. А. Мартиросян
Решение нелинейной оптической задачи для
квазимонохроматической
волны вблизи каустики в осесимметричном случае
(Представлено 25/II 2004)
Рассматривается осесимметричная задача для
квазимонохроматической волны вблизи каустики. В линейном случае лучи имеют
огибающую, или каустику, на которой в момент t имеются падающая и отраженная
волны (рис. 1,2), пересекающие каустику в точке A, радиус-вектор которой
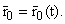 Как показывает линейное решение для
произвольной линейной гиперболической системы уравнений с переменными
коэффициентами [1,2] и для волнового уравнения с переменной скоростью волн
[3,4], вблизи каустики задача в оснoвном порядке определяется координатами
Как показывает линейное решение для
произвольной линейной гиперболической системы уравнений с переменными
коэффициентами [1,2] и для волнового уравнения с переменной скоростью волн
[3,4], вблизи каустики задача в оснoвном порядке определяется координатами
|
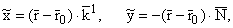
|
(1) |
где
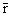 - радиус-вектор точки (xi),
- радиус-вектор точки (xi),
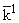 = (ai1),
= (ai1),
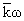 - волновой вектор в точке A,
w - частота волны,
- волновой вектор в точке A,
w - частота волны,
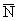 - единичный вектор нормали к каустике в точке A, направленный в сторону ее
выпуклости,
- единичный вектор нормали к каустике в точке A, направленный в сторону ее
выпуклости,
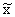 - эйконал, или время пробега волны от точки A до точки
(xi).
- эйконал, или время пробега волны от точки A до точки
(xi).
Вначале рассмотрим линейный дифференциальный
оператор
D0(iPt, -iPxj,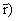 f =
0, f =
0, |
|
(2) |
где согласно (1) в основных порядках
малости
|
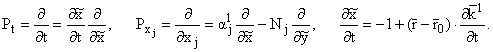 |
(3) |
Разлагая (2), (3) по степеням малых
операторов, оставляя только старшие производные от F,
т. е. не учитывая действия операторов на переменные коэффициенты, с операторами
можно проводить действия, как с числами, и получить, полагая F = y(y1)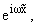
|
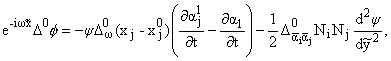
|
(4) |
где согласно уравнению лучей [1]
|
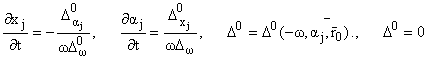 |
(5) |
есть дисперсионное соотношение,
индекс при D0 обозначает дифференцирование.
Применим теперь полученные соотношения к нелинейной оптической среде, где в
осесимметричной задаче имеет место уравнение для электрического поля [1], [5]
|
_
E
|
= |
1
2
|
|
_
E
|
1
|
+ kc, |
_
E
|
1
|
= E1 · |
_
e
|
, DE1 = |
1
c2
|
|
¶2
¶t2
|
{ e0 + (e2 + ie1)|E1|2}E1, E1 =
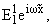 | |
(6) |
где
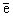 - единичный вектор поляризации волны, D = [(¶2)/(¶r2)]+[1/r][(¶)/(¶r)]+[(¶2)/(¶x2)], D - оператор
Лапласа, x - осевая, r - радиальная координаты. Линейное поглощение считается
малым и не учтено в (6).
- единичный вектор поляризации волны, D = [(¶2)/(¶r2)]+[1/r][(¶)/(¶r)]+[(¶2)/(¶x2)], D - оператор
Лапласа, x - осевая, r - радиальная координаты. Линейное поглощение считается
малым и не учтено в (6).
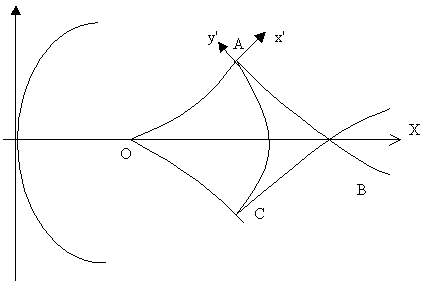
Рис. 1. Случай начальной волны в форме параболоида.
Обозначая через r0 значения r на
зеркале (рис. 1,2), введя функцию U, E1 =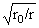 · U, можно из (6) для немалых r,
соответствующих окрестности каустики вдали от оси x, получить в основных
порядках уравнение
· U, можно из (6) для немалых r,
соответствующих окрестности каустики вдали от оси x, получить в основных
порядках уравнение
|
¶2U
¶r2
|
+ |
¶2 U
¶x2
|
- |
1
c2
|
|
¶2
¶t2
|
(e0U) = |
1
c2
|
|
¶2
¶t2
|
(e2 + ie1) |
r0
r
|
|U|2, | |
(7) |
где отброшено малое
недифференцируемое слагаемое от U.
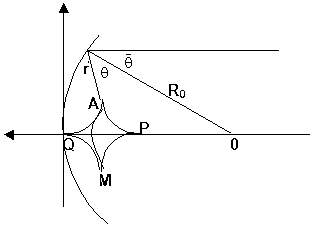
Рис. 2. Случай сферического зеркала. РА, РМ -
каустика, АМ - падающая волна, AQ,
MQ - отраженные от каустики волны.
Обозначая левую часть (7) через D0U, x1 = x, x2 = r, можно с
учетом (5) получить дисперсионное соотношение
|
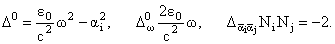
|
(8) |
Записывая u = y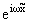 , учитывая
(4), можно уравнение (7) записать в виде
, учитывая
(4), можно уравнение (7) записать в виде
|
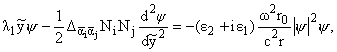
|
(9) |
| где l1 = wDw |
ж
з
и |
Nj - |
aiNi
akDak
|
Daj |
ц
ч
ш |
|
ж
з
и |
|
¶a1j
¶t
|
- |
¶aj
¶t
|
ц
ч
ш |
.
| |
(10) |
Для оптической среды в силу (8)
имеет место соотношение изотропии w = w(k), k2 = a2i, и можно получить [6]
|
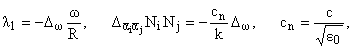
|
(11) |
где [1/R] есть разность кривизны
луча и каустики. Правую часть (9) можно записать в виде
| Dw |
ж
з
и |
|
¶W
¶a2
|
ц
ч
ш |
0
|
|
r0
r
|
|y|2y. | |
(12) |
Здесь согласно определению (8), (9), (12) (
[(¶W)/(¶a2)])0 = -[(e2 + ie1)/(2e0)]w есть коэффициент
при a2 = [(r0)/r]|y|2 в нелинейной частоте
W, W = w + ([(¶W)/(¶a2)])0a2.
Вводя безразмерные переменные y*,
y*, получим
|
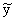 = c-[1/3]y*,
y = my* = c-[1/3]y*,
y = my*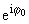 , j0 = , j0 = |
p
2
|
(kў + 1) - |
p
4
|
, c = |
2k2
R
|
, k2 = |
w2
c2n
|
, | |
(13) |
где c =
[(l1)/( [1/2]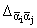 NiNj)] = [(2k2)/R],
k = [(w)/(cn)],
NiNj)] = [(2k2)/R],
k = [(w)/(cn)],
m =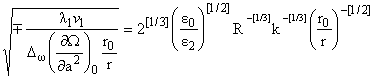 , n1 = c-[1/3], , n1 = c-[1/3],
|
|
(14) |
где последние соотношения для c, m в (14) соответствуют оптической
среде, знаки под корнем квадратным соответствуют ([(¶W)/(¶a2)] )0 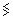 0.
0.
В случае оптической среды в силу (9), (12)
([(¶W)/(¶a2)] )0 < 0. Подставляя (13),(14) в
(9), (10), можно получить для оптической среды уравнение
|
d2y*
dy*2
|
- y*y* + |y*|y* |
ж
з
и |
1 + |
ie1
e2
|
ц
ч
ш |
= 0. | |
(15) |
Линейное решение записывается через
функцию Эйри [1-6]
y0 =
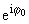 Cv(y*),
C = 2a1[1/12]A1w-kў-[5/6], a1 = Cv(y*),
C = 2a1[1/12]A1w-kў-[5/6], a1 = |
c
w2
|
. | |
(16) |
С учетом (13), записывая (16) вдали
от каустики для больших -y* > 0, можно
получить решение геометрической оптики
yгеом =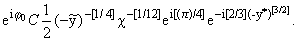 |
|
(17) |
Для определения C или A через
начальную амплитуду волны запишем линейное решение вдали от каустики для
однородной среды. Уравнения лучей имеют вид [7]
|
| x - x0(q) = cn(t - t0 - t)cosq, | |
| r - r0(q) = cn(t - t0 - t)sinq, | | |
| |
(18) |
где t = 0
- фронт волны, t0(q) - момент прихода волны
на каустику, x = x0(q), r = r0(q) - уравнение каустики, кривизна которой равна
[1/(cntў0(q))] = -[1/R]. Вблизи каустики для
малых qў = q - q1, где q1 -
значение q для фиксированного луча, получено [7]
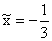 tў0(q)qў3 + t, tў0(q)qў3 + t,
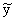 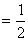 cntў0(q)qў2. cntў0(q)qў2. | |
(19) |
Решение геометрической оптики
записывается в виде
yгеом =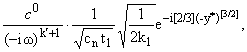 t1 = t0ў(q)qў,
t1 = t0ў(q)qў, | |
(20) |
где [(c0)/((-iw)kў+1)] - значение начальной амплитуды волны,
2k1 - начальная кривизна меридианального сечения волны или зеркала. В
силу (19), (20)
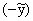 -[1/4] = 21/4 -[1/4] = 21/4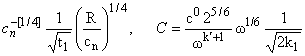 R-[1/3]cn-[1/6]. R-[1/3]cn-[1/6]. |
|
(21) |
Учитывая (14), получим
|
C
m
|
= |
c0
wkў+1
|
· 21/2w1/2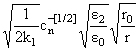 |
. | |
(22) |
Таким образом характерный множитель
в линейном решении (13), (22) не зависит от [1/R] и имеет четкое значение. В
(22) r = r(t) есть значение r на каустике в точке A.
Для определения решения уравнения Пенлеве,
получаемого из (15) при e1 = 0, нужно
поставить граничные условия, взятые из линейного решения (16) в некоторых
точках, например, y* = ±5, y*(±5) = [C/(m)]v(±5). В силу сложности граничной
задачи задавались начальные условия
| y*(5) = |
C
m
|
v(5), |
dy*
dy*
|
к
к
к |
y* = 5
|
= |
C
m
|
vў(5) | |
(23) |
и проводился расчет уравнения (15)
при e1 = 0
|
d2y*
dy*2
|
- y*y* + y*3 = 0 | |
(24) |
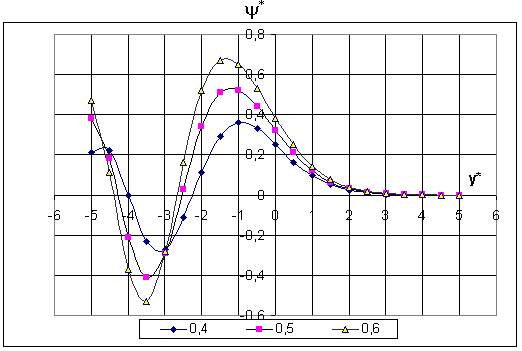
для значений [C/(m)] = 0.4; 0.5; 0.6 (решение приведено на
рис. 3), причем условие y*(-5) = [C/(m)]v(-5) удовлетворено достаточно точно, полученное решение
годится для начальной сходящейся волны в форме параболоида с уравнением
x1 = k1r12 (рис. 1), причем
2k1 есть кривизна меридианального сечения в начальной точке
r1 = 0. Расчет для начального условия (23), взятого в точке
y* = -5, не дал удовлетворительного выполнения
граничных условий в точке y* = 5, поэтому в работе рассмотрено условие
(23), взятое в точке y* = 5. Линейное решение дает такую же картину
кривой, как и на рис. 3, но с несколько меньшими по модулю ординатами.
Рис. 3. Нелинейное решение для квазимонохроматической
волны вблизи каустики.
В случае сферического зеркала радиуса
R0 (рис. 2) при наличии параллельного оси x пучка лучей,
падающих на зеркало, для отраженных от зеркала лучей имеем
x = x0 -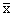 , x0 = R0cos , x0 = R0cos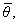 r = r0 - r = r0 -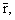 r0 = R0sin r0 = R0sin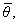 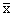 = rўcos = rўcos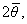 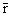 = rўsin = rўsin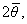 |
|
(25) |
где x0, r0
есть координаты точек пересечения лучей со сферическим зеркалом, rў = cn( t -[(R0cos )])/(cn)]). Соотношения (25) можно записать в
виде
)])/(cn)]). Соотношения (25) можно записать в
виде
Уравнения огибающей
этих лучей, или каустики, имеют вид:
x sin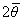 = r cos = r cos + R0sin + R0sin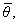 x cos x cos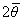 +
r sin +
r sin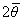 |
= |
R0
2
|
cos |
. | |
(26) |
Характерные точки для полученной
каустики
|
 = 0, x = = 0, x = |
R0
2
|
, r = 0, |
= |
p
4
|
, r = |
R0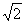
4
|
, x = |
R0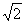
2
|
,  |
= |
p
2
|
, x = 0, r = R0. | |
(27) |
Каустика изображена на рис. 2. В
отличие от случая сходящейся начальной волны в форме параболоида (рис. 1),
при котором каустики [8] выражаются уравнением
|
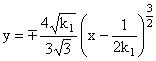
|
(28) |
и расположены после фокальной
точки, в случае сферического зеркала каустика (26) расположена до фокуса y = 0,
x = R0. Уравнение каустики для сферического зеркала впервые получено
академиком П.М. Геруни [8]. Для случая параболоида до каустики (28) имеются
фокальные точки на оси x [9]. Однако решение вблизи каустики (28) вдали от оси x
будет по-прежнему даваться (24), (22).
Институт механики НАН РА
Литература
1. Багдоев А.Г. Распространение волн в сплошных средах. Ереван. 1981. 307
с.
2. Ludwig D. - Сommun. pure Appl. Math. 1966. V. 19. N6. P.
215.
3. Кравцов Ю.А. - Изв. высших учебных заведений. Радиофизика. 1964. В.
4.
4. Газарян Ю.Л. В сб.: Динамическая теория распространения сейсмических волн. ЛГУ. 1961.
Т. 5. С. 73-114.
5. Мартиросян
Г.А. - Информационные технологии и управление. 2002. N4. С.
86-93.
6. Багдоев А.Г., Саакян
С.Г. - Акустический журнал. 2000. Т. 46. N3. С.
299-305.
7. Багдоев А.Г.
- Изв. АН АрмССР. Техн. науки. 1967. Т. 20. N3.
С. 26-29.
8. Геруни П.М.
Автореф. канд. дис. 1961.
М.
9. Фридлендер Ф. Звуковые импульсы. М. ИЛ. 1962. 232 с.
![]() - радиус-вектор точки (xi),
- радиус-вектор точки (xi),
![]() = (ai1),
= (ai1),
![]() - волновой вектор в точке A,
w - частота волны,
- волновой вектор в точке A,
w - частота волны,
![]() - единичный вектор нормали к каустике в точке A, направленный в сторону ее
выпуклости,
- единичный вектор нормали к каустике в точке A, направленный в сторону ее
выпуклости,
![]() - эйконал, или время пробега волны от точки A до точки
(xi).
- эйконал, или время пробега волны от точки A до точки
(xi). ![]() f =
0,
f =
0,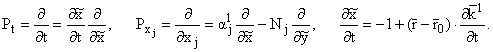
![]()
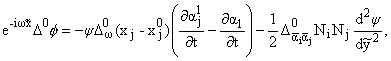
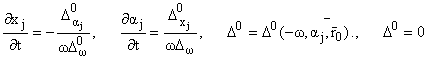
![]()
![]() - единичный вектор поляризации волны, D = [(¶2)/(¶r2)]+[1/r][(¶)/(¶r)]+[(¶2)/(¶x2)], D - оператор
Лапласа, x - осевая, r - радиальная координаты. Линейное поглощение считается
малым и не учтено в (6).
- единичный вектор поляризации волны, D = [(¶2)/(¶r2)]+[1/r][(¶)/(¶r)]+[(¶2)/(¶x2)], D - оператор
Лапласа, x - осевая, r - радиальная координаты. Линейное поглощение считается
малым и не учтено в (6). ![]() · U, можно из (6) для немалых r,
соответствующих окрестности каустики вдали от оси x, получить в основных
порядках уравнение
· U, можно из (6) для немалых r,
соответствующих окрестности каустики вдали от оси x, получить в основных
порядках уравнение ![]()
![]() , учитывая
(4), можно уравнение (7) записать в виде
, учитывая
(4), можно уравнение (7) записать в виде 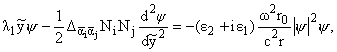
![]()
![]() = c-[1/3]y*,
y = my*
= c-[1/3]y*,
y = my*![]() , j0 =
, j0 =![]() NiNj)] = [(2k2)/R],
k = [(w)/(cn)],
NiNj)] = [(2k2)/R],
k = [(w)/(cn)], 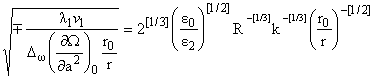 , n1 = c-[1/3],
, n1 = c-[1/3],
0.
![]() Cv(y*),
C = 2a1[1/12]A1w-kў-[5/6], a1 =
Cv(y*),
C = 2a1[1/12]A1w-kў-[5/6], a1 =![]()
![]() tў0(q)qў3 + t,
tў0(q)qў3 + t,
![]()
![]() cntў0(q)qў2.
cntў0(q)qў2.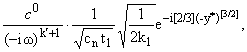 t1 = t0ў(q)qў,
t1 = t0ў(q)qў,![]() -[1/4] = 21/4
-[1/4] = 21/4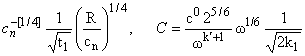 R-[1/3]cn-[1/6].
R-[1/3]cn-[1/6].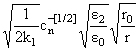
![]() , x0 = R0cos
, x0 = R0cos![]() r = r0 -
r = r0 -![]() r0 = R0sin
r0 = R0sin![]()
![]() = rўcos
= rўcos![]()
![]() = rўsin
= rўsin![]()
![]() )])/(cn)]). Соотношения (25) можно записать в
виде
)])/(cn)]). Соотношения (25) можно записать в
виде ![]()
![]() = r cos
= r cos![]() + R0sin
+ R0sin![]() x cos
x cos![]() +
r sin
+
r sin![]()
![]()
![]() = 0, x =
= 0, x =![]()
![]()
![]()
![]()