УДК 519.1

   В работе рассматриваются неориентированные графы без кратных ребер и петель. Не определяемые в работе понятия и обозначения можно найти в [1-3].
   Множество вершин графа G обозначается через V(G), множество ребер - E(G), максимальная из степеней вершин G - D(G), хроматический класс - cў(G). Для вершины v О V(G) определим множество J(v) Н V(G) следующим образом: J(v) = { u О V(G)|(u,v) О E(G)}.
   Функция f:E(G)® N называется правильной реберной раскраской графа G, если для любых двух смежных ребер e₁ О E(G) и e₂ О E(G) f(e₁) № f(e₂).
   Правильную реберную раскраску f графа G назовем равновесной t-раскраской, если для каждого i, 1 Ј i Ј t, существует хотя бы одно ребро e_i О E(G), для которого f(e_i) = i, и для любых двух вершин v₁ О V(G), v₂ О V(G)

   Для t і 1 через ( m)_t обозначим множество всех графов, для которых существует равновесная t-раскраска. Обозначим: ( m) є 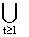( m)_t. Для графа G О ( m) обозначим через w(G) и W(G), соответственно, наименьшее и наибольшее значение t , при котором G О ( m)_t.
   Ясно, что для G О ( m) w(G) і D(G), W(G) Ј |E(G)|. Отсюда и из теоремы Турана [1] следует
   Утверждение 1. Если G О ( m) и G не имеет треугольников, то W(G) Ј Ј ë[(|V(G)|²)/4] û.
   Лемма. Если G регулярный граф и cў(G) = D(G), то G О ( m) и w(G) = D(G).
   Доказательство. Рассмотрим правильную реберную раскраску f графа G в цвета 1,2,ј,D(G). Так как G регулярный граф, то f является равновесной D(G) - раскраской. Отсюда вытекает, что G О (m) и w(G) Ј D(G).
   Лемма доказана.
   Следствие 1. При   n і 2  C_2n О ( m),  w(C_2n) = W(C_2n) = 2.
   Следствие 2. При  n і 1   K_2n О ( m),  w(K_2n) = 2n - 1.
   Следствие 3. При  n і 1   Q_n О ( m),  w(Q_n) = n
   Среди регулярных графов G с cў(G) = D(G) + 1 существуют графы, удовлетворяющие условию G О (m), и существуют графы, удовлетворяющие условию G П ( m).
   Утверждение 2. При  n і 2   C_2n+1 П ( m).
   Утверждение 3. Если  G  есть  граф  Петерсена [1],  то   G О ( m).
   Доказательство. Пусть V(G) = {x₁,x₂,x₃,x₄,x₅,y₁,y₂,y₃,y₄,y₅}, E(G) = {(x₁,x₂), (x₂,x₃), (x₃,x₄), (x₄,x₅), (x₅,x₁), (y₁,y₃), (y₃,y₅), (y₅,y₂), (y₂,y₄), (y₄,y₁), (x₁,y₁), (x₂,y₂), (x₃,y₃), (x₄,y₄), (x₅,y₅)}. Определим раскраску f ребер графа G следующим образом:
f((x₁,x₂)) = 7, f((x₂,x₃)) = 2, f((x₃,x₄)) = 3, f((x₄,x₅)) = 6, f((x₅,x₁)) = 1,
f((y₁,y₃)) = 3, f((y₃,y₅)) = 2, f((y₅,y₂)) = 5, f((y₂,y₄)) = 4, f((y₄,y₁)) = 5,
f((x₁,y₁)) = 2, f((x₂,y₂)) = 1, f((x₃,y₃)) = 5, f((x₄,y₄)) = 1, f((x₅,y₅)) = 3.
   Нетрудно убедиться, что f является равновесной 7-раскраской ребер графа G.
   Утверждение 3 доказано.
   Теорема 1. При  n і 1
          1. K_n,n О ( m);

          2. w(K_n,n) = n;
          3. W(K_n,n) =

   Доказательство. Так как K_n,n при любом n О N является регулярным графом, удовлетворяющим
равенству cў(K_n,n) = D(K_n,n) = n, то из леммы вытекают утверждения 1 и 2 доказываемой теоремы.
   Утверждение 3 доказываемой теоремы при n Ј 2 очевидно. Докажем, что оно верно при n і 3.
Заметим, что каждому магическому [2] квадрату порядка n можно сопоставить равновесную n²-
раскраску ребер графа K_n,n. Так как для любого n і 3 существует [2] магический квадрат порядка
n, то при n і 3 W(K_n,n) і n² = |E(K_n,n)|.
   Теорема 1 доказана.
   Следствие 4. Для  графов  K_n,n  при  n і 3  оценка  утверждения 1 достижима.
   Теорема 2. При  m і 2   W(K_4m) і W(K_2m) + 4m².
   Доказательство. Пусть V(K_4m) = {x₁,x₂,ј,x_4m}.
   Пусть G₁ есть подграф графа K_4m, порожденный вершинами x₁,x₂,ј,x_2m. Ясно, что G₁
изоморфен графу K_2m и, следовательно, ввиду следствия 2, существует равновесная W(K_2m)-
раскраска f₁ ребер графа G₁.
   Пусть G₂ есть подграф графа K_4m, порожденный вершинами x_2m+1,x_2m+2,ј,x_4m.
   Определим подграф G₃ графа K_4m следующим образом:

V(G3) є V(K4m);    E(G3) є E(K4m)\(E(G1)ИE(G2)).

   Легко видеть, что G₃ изоморфен полному двудольному графу K_2m,2m и, следовательно, ввиду
теоремы 1, G₃ О ( m). Пусть f₂ есть равновесная 4m²-раскраска ребер графа G₃.
   Определим раскраску F ребер графа K_4m.
   Для i = 1,2,ј,4m и j = 1,2,ј,4m при i № j положим:

F((xi,xj)) = м п н п о f1((xi,xj)), если 1 Ј i Ј 2m, 1 Ј j Ј 2m; f1((xi-2m,xj-2m)), если 2m + 1 Ј i Ј 4m, 2m + 1 Ј j Ј 4m; f2((xi,xj)) + W(K2m), если 1 Ј i Ј 2m, 2m + 1 Ј j Ј 4m.

   Легко видеть, что F является равновесной (4m² + W(K_2m))-раскраской ребер графа K_4m.
   Теорема 2 доказана.
   Следствие 5. При m і 2 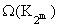 і [(2^2m - 7)/3].

   Доказательство. По теореме 2

W(K2m) і W(K2m-1) + 22(m-1) W(K2m-1) і W(K2m-2) + 22(m-2) ................................................. W(K8) і W(K4) + 22·2.

Складывая эти неравенства, получим:
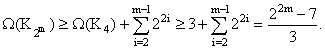
   Следствие 5 доказано.
   Следствие 6. При  m і 2   W(K_4m) і 4m² + 2m - 1.
   Утверждение 4. Для p і 2 существует граф G О ( m), для которого W(G) і |V(G)| + p.
   Доказательство. По данному p і 2 выберем m, удовлетворяющее неравенству 4m² - 2m - 1 і p.
Положим G є K_4m. По следствию 6 W(G) і 4m² + 2m - 1 = 4m² - 2m - 1 + |V(G)| і |V(G)| + p.
   Утверждение 4 доказано.
   Утверждение 5. Для  p і 3  существует  граф   G О ( m),  для  которого W(G) - w(G) і p.
   Доказательство. По данному p і 3 выберем m, удовлетворяющее неравенству 4m² - 2m і p.
Положим G є K_4m. Из следствий 2 и 6 получим: W(G) і 4m² + 2m - 1 = 4m² - 2m + 4m - 1 і p + w(G).
   Утверждение 5 доказано.
   Настоящее исследование поддержано целевой программой 04-10- 31 РА.

     Институт проблем информатики и автоматизации НАН РА

Литература

     1. Harary F.  Graph Theory. Addison-Wesley. Reading. MA. 1969.
     2. Постников М.М.  Магические квадраты. М. Наука. 1964.
     3. Визинг В.Г.  Хроматический класс мультиграфа. Кибернетика. 1965. N3. С. 29-39.

---