МАТЕМАТИКА
УДК 517.538.5
А. З. Мартиросян
Лакунарные аналоги теоремы Рунге и многократно
T-универсальные функции,
представимые лакунарными степенными
рядами, в пространстве голоморфных функций
(Представлено академиком Н. У. Аракеляном 22/I 2005)
1. Для компактного
множества K из конечной комплексной плоскости C обозначим через A(K) Банахово
пространство из всех непрерывных на K и голоморфных на его внутренности
комплексно значных функций с нормой ||f|| = sup{|f(z) | : z О K}. Обозначим через M
семейство всех компактных множеств K М C со связным
дополнением C \ K. Для множества E М C будем обозначать
¶E ее границу. Пусть N, Z будут, как обычно, множества
из всех натуральных и целых чисел, соответственно; пусть также
N0 = N З {0}. Для последовательности
Q =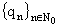 из
N0 положим n(t) - количество ее членов из отрезка и определим
плотность, верхнюю плотность и минимальную плотность для Q, соответственно,
следующим образом:
из
N0 положим n(t) - количество ее членов из отрезка и определим
плотность, верхнюю плотность и минимальную плотность для Q, соответственно,
следующим образом:
| D(Q) = |
lim
t®Ґ
|
|
n(t)
t
|
, |
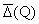 = = |
lim
t®Ґ
|
|
sup
|
|
n(t)
t
|
, Dmin(Q) = |
t®1-0
|
t®Ґ
|
|
n(t) - n(tt)
t(1 - t)
|
. | |
Пусть функция f голоморфна в односвязной
области G М C. Последовательность операций
{Lj}jОZ определим следующим
образом: для z О G и j О
N0 положим L0f(z) = f(z), L1f(z) = (zf(z))ў, Ljf(z) = L1(Lj-1f(z)) при j = 2, 3, ј; для z
О G и j = -1, -2, ј положим
где
интеграл берется по любой спрямляемой дуге из G, соединяющей, соответственно, 0
или z0 c z.
Пусть O М C -
открытое множество, H(O) - совокупность всех голоморфных на O функций.
Рассмотрим последовательность {Kn}nОN компактных подмножеств, исчерпывающих O, т.е. Kn М Kn+1 и ИnОNKn = O. Для функции h О H(O) и любого n О N положим
| dn(h) = |
max
zОKn
|
|h(z)|, d(h) = |
Ґ
е
n=1
|
|
dn(h)
2n(1 + dn(h))
|
. | |
Если
h1,h2 О H(O), то определим
расстояние между ними как r(h1,h2) = d(h1 - h2). Множество H(O), снабженное такой метрикой,
есть пространство Фреше; для последовательности {hk}kОN М H(O) имеем
тогда
и только тогда, когда {hk}kОN
сходится к h локально-равномерно в O. Итак, r -
естественная метрика, индуцирующая локально-равномерную сходимость в H(O).
Для заданных открытого множества O М C, 0 О O, и подпоследовательности
Q М N0 обозначим через HQ(O)
подпространство из всех функций j О H(O), представимых в некоторой окрестности нуля лакунарным
степенным рядом.
| j(z) = |
Ґ
е
n=0
|
jzzn, jn = 0 при
n П
Q. | |
Определение
1. Пусть O М C - произвольное
открытое множество. Функция j О H(O) называется T-универсальной на O ("универсальной
относительно трансляций"), если она имеет следующее свойство: для всех K О M, для всех f О A(K) и для всех
V О ¶O существуют последовательности {an}nОN и {bn}nОN такие, что anz+bn О O
для
всех z О K и всех n О N,
последовательность {anz + bn}nОN сходится к z
и
последовательность {j(anz + bn)}nОN сходится к f(z) равномерно на K.
Определение
2. Пусть O М C, 0 О O - произвольное открытое множество, Q М N0 - произвольная подпоследовательность. Функция
j О H(O) называется
многократно T-универсальной относительно последовательности операций
{Lj}jОZ, если при любом
фиксированном j О Z функция Ljj(z) О HQ(O) и
T-универсальна.
Множество всех универсальных по определению 2
функций обозначим через UQ(O). Это множество исследовалось в [1, 2],
а именно: при тех или иных предположениях относительно O и Q было доказано, что
UQ(O) № Ж. В данной
работе множество UQ(O) изучается количественно: оказывается, что
UQ(O) плотно в HQ(O) при весьма общих предположениях на O
и Q. При этом существенно используются лакунарные аналоги теоремы К. Рунге об
аппроксимации многочленами.
Отметим, что похожие вопросы конструирования
многократно универсальных функций без контроля лакун их степенных рядов
исследовались В. Лухом (см. [3, 4]). Отметим также, что подробную информацию о
развитии теории универсальных функций и полную библиографию вплоть до 1999 г.
можно найти в обзоре К. Гроссе-Эрдмана [5]. Более поздние примыкающие
исследования представлены, например, в [6-12].
2. Для заданной
подпоследовательности Q М N0 обозначим через
PQ множество всех лакунарных многочленов, содержащих только степени
{zn, n О Q}.
Теорема 1. Пусть Q(0 О Q) -
подпоследовательность из
N0 с плотностью D(Q) = 1 и O № C - открытое множество с односвязными компонентами, 0 О O. Тогда PQ плотно в HQ(0).
Теорема 2. Пусть Q(0 О Q) -
подпоследовательность из
N0 с верхней плотностью
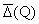 = 1, O № C - открытое множество
с односвязными компонентами, причем 0 О O и содержащая
0 компонента является звездою относительно точки 0. Тогда PQ
плотно в HQ(O).
= 1, O № C - открытое множество
с односвязными компонентами, причем 0 О O и содержащая
0 компонента является звездою относительно точки 0. Тогда PQ
плотно в HQ(O).
Доказательство теорем 1,
2. Пусть {K}1Ґ
исчерпывающая O последовательность компактных подмножеств, т.е. Kn
М Kn+1 и
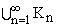 = O. В предположениях теорем 1, 2 подмножества Kn можно
выбрать так, чтобы 0 О K и Kn имело связное
дополнение C \ Kn (n О N). Более того, в
случае теоремы 2 можно считать, что для каждого Kn содержащая 0 ее
компонента является звездою относительно точки 0.
= O. В предположениях теорем 1, 2 подмножества Kn можно
выбрать так, чтобы 0 О K и Kn имело связное
дополнение C \ Kn (n О N). Более того, в
случае теоремы 2 можно считать, что для каждого Kn содержащая 0 ее
компонента является звездою относительно точки 0.
Достаточно доказать, что любая функция из
HQ(Kn) приближается равномерно на Kn
многочленами из PQ. Однако это утверждение в случае теоремы 1 следует
из леммы работы [7], а в случае теоремы 2 - из леммы работы [8]. Теоремы 1, 2
доказаны.
Теоремы 1, 2 являются лакунарными аналогами
аппроксимационной теоремы К. Рунге. Частный случай теоремы 1, когда
O-односвязная область, совпадает с одним результатом Кореваара и Диксона (см.
[13]).
3. Теорема 3. Пусть Q - подпоследовательность из N0
с плотностью D(Q) = 1 и O № C - открытое множество
с односвязными компонентами, 0 О O. Тогда множество
UQ(O) плотно в HQ(O).
Доказательство. 1. Согласно теореме 3 из [2] имеем UQ(O) №
Ж. Пусть j - произвольная
функция из UQ(O).
a) Отметим сперва, что множество
UQ(O) содержит также функцию gj, где g №
0 - произвольная постоянная.
b) Убедимся теперь, что UQ(O)
содержит также функцию jp := j + p, где p - произвольный многочлен из PQ. В самом
деле, пусть заданы произвольные j О Z, граничная точка
V О ¶O, компактное множество K О M и
функция f О A(K). Выберем Ljj для j на O так, чтобы
Ljjp(z) = Ljj(z) + Ljp(z) при z О O
(при j О N0 выполнение этого условия
очевидно).
Предположим сперва, что V № Ґ. Так
как j О UQ(O), то
существуют последовательности {an}1Ґ и {bn}1Ґ с an ® 0, bn ® z, при n ® Ґ такие, что anz + bn О O для всех z О K и n О N, а последовательность {Ljj(anz + bn)}1Ґ сходится к f(z) - Ljp(V) равномерно на K.
Отсюда вытекает, что последовательность {Ljjp(anz + bn)}1Ґ сходится к f(z) равномерно на K, т.е. jp О UQ(O).
Предположим теперь, что V = Ґ. Тогда можем выбрать
последовательность {Vm} с Vm О ¶OЗC и Vm ® Ґ при m ® Ґ.
Для каждого m О N существуют последовательности
{an(m)}nОN и
{bn(m)}nОN с
an(m) ® 0,
an(m) ® Vm при n ® Ґ такие, что
an(m)z + bn(m) О O для всех z О K и n О N, а последовательность {Ljj(an(m)z + bn(m))}1Ґ сходится к f(z) - Ljp(Vm)
равномерно на K. Для каждого m О N найдется
nm > m (nm О N) такое, что для
am :=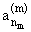 ,
bm :=
,
bm :=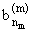 одновременно будут выполняться следующие условия:
одновременно будут выполняться следующие условия:
|
| |am| < |
1
m
|
, |bm - Vm| < |
1
m
|
, | |
|
max
K
|
|LjP(amz + bm) - Lj(Vm)| < |
1
m
|
, | |
|
max
K
|
|Ljj(amz + bm) - f(z) + Ljj(Vm)| < |
1
m
|
. | | |
| |
Очевидно, что am ® 0, bm ® V = Ґ при m ® Ґ и последовательность
{Ljjp(amz + bm)}1Ґ сходится к f(z) равномерно на K. Поэтому jp О UQ(O).
2. Чтобы доказать теорему 3, нужно
показать, что для каждой функции F О HQ(O) и
любого e > 0 существует T-универсальная функция
j О UQ(O), для
которой r(j,F) < e. Если взять произвольную функцию j0 О UQ(O), то
очевидно, что
 = 0. Поэтому можно выбрать постоянную g > 0 так, чтобы d(gj0) < [(e)/2].
Согласно теореме 1 существует последовательность {Pk} многочленов из
PQ, которая сходится к F локально-равномерно на O. Значит, найдется
многочлен p О PQ с r(p,F) < e/2. По шагу 1 функция
j(z) := gj0(z) + p(z) содержится в UQ(O) и
удовлетворяет оценке
= 0. Поэтому можно выбрать постоянную g > 0 так, чтобы d(gj0) < [(e)/2].
Согласно теореме 1 существует последовательность {Pk} многочленов из
PQ, которая сходится к F локально-равномерно на O. Значит, найдется
многочлен p О PQ с r(p,F) < e/2. По шагу 1 функция
j(z) := gj0(z) + p(z) содержится в UQ(O) и
удовлетворяет оценке
| r(j,F) = r(gj0 + r,F) Ј d(gj0) + r(r,F) < e. | |
Теорема
3 доказана.
Теорема 4. Пусть Q - подпоследовательность из N0
с верхней плотностью
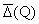 = 1, O № C - открытое множество с односвязными компонентами, причем
0 О O и содержащая 0 компонента является звездою
относительно точки 0. Тогда множество UQ(O) плотно в HQ(O).
= 1, O № C - открытое множество с односвязными компонентами, причем
0 О O и содержащая 0 компонента является звездою
относительно точки 0. Тогда множество UQ(O) плотно в HQ(O).
Для случая круга DR = {z : |z| < R}, где 0 < R < Ґ, имеем следующий результат.
Теорема 5. Пусть Q - подпоследовательность из N0
с минимальной
плотностью Dmin(Q) > 0. Тогда множество
UQ(DR) плотно в HQ(DR).
Теоремы 4, 5 доказываются точно так же, как
теорема 3. Различие в докозательстве теоремы 4 состоит в том, что вместо теоремы
1 нужно использовать теорему 2, а вместо теоремы 3 из [2] - соответствующий
аналогичный результат. Что касается теоремы 5, то для ее доказательства вместо
теоремы 3 из [2] надо применить теорему 2 из [7] (плотность PQ в
HQ(DR) очевидна, поскольку в DR частичные суммы
любого степенного ряда с центром в нуле сходятся к сумме этого ряда локально
равномерно в DR).
Ереванский государственный университет
Литература
1. Мартиросян В.А., Мартиросян А.
З. - Изв. НАН Армении. 2004. Математика. Т. 39.
N3.
2. Мартиросян В.А.,
Мартиросян А. З. - ДНАН Армении. 2005. Т. 105. N1.
С. 17-20.
3. Luh W.
- Complex Variables. 1996. V. 31. P.
87-96.
4. Luh W. - J. Approxim. Theory. 1997. V. 89. P.
135-155.
5. Grosse-Erdmann K.G.
- Bull. Amer. Math. Soc. 1999. V. 36. P.
345-381.
6. Luh W., Martirosian
V. A., Muller J. - Indagationes Mathem. (N.S.) 1998. V. 9.
P. 529-536.
7. Luh W.,
Martirosian V.A., Muller J. - Acta Sci. Math. (Szeged).
1998. V. 64. P. 67-79.
8. Luh W.,
Martirosian V.A., Muller J. - Journal of Approxim. Theory.
2002. V. 114. P. 201-213.
9. Gharibyan T., Luh W., Muller J. - Analysis. 2003. V.
23. P. 199-214.
10. Gharibyan
T., Luh W. - Annales Univ. Sci. Budapest. Sect.Comp. 2003.
V. 22. P. 113-126.
11. Гарибян
Т., Лу В. - Изв. НАН Армении. Математика. 2003. Т. 38. N4.
С. 51-64.
12. Шилингс Б.
- Изв. НАН Армении. Математика. 2003. Т. 38. N4. С.
85-94.
13. Dixon M., Korevaar J.
- Proc. Kon. Neder. Akad. Wetensch. 1977. V. A80. N3. P.
176-194.
![]() = 1, O № C - открытое множество
с односвязными компонентами, причем 0 О O и содержащая
0 компонента является звездою относительно точки 0. Тогда PQ
плотно в HQ(O).
= 1, O № C - открытое множество
с односвязными компонентами, причем 0 О O и содержащая
0 компонента является звездою относительно точки 0. Тогда PQ
плотно в HQ(O). ![]() = O. В предположениях теорем 1, 2 подмножества Kn можно
выбрать так, чтобы 0 О K и Kn имело связное
дополнение C \ Kn (n О N). Более того, в
случае теоремы 2 можно считать, что для каждого Kn содержащая 0 ее
компонента является звездою относительно точки 0.
= O. В предположениях теорем 1, 2 подмножества Kn можно
выбрать так, чтобы 0 О K и Kn имело связное
дополнение C \ Kn (n О N). Более того, в
случае теоремы 2 можно считать, что для каждого Kn содержащая 0 ее
компонента является звездою относительно точки 0. ![]() ,
bm :=
,
bm :=![]() одновременно будут выполняться следующие условия:
одновременно будут выполняться следующие условия: ![]() = 0. Поэтому можно выбрать постоянную g > 0 так, чтобы d(gj0) < [(e)/2].
Согласно теореме 1 существует последовательность {Pk} многочленов из
PQ, которая сходится к F локально-равномерно на O. Значит, найдется
многочлен p О PQ с r(p,F) < e/2. По шагу 1 функция
j(z) := gj0(z) + p(z) содержится в UQ(O) и
удовлетворяет оценке
= 0. Поэтому можно выбрать постоянную g > 0 так, чтобы d(gj0) < [(e)/2].
Согласно теореме 1 существует последовательность {Pk} многочленов из
PQ, которая сходится к F локально-равномерно на O. Значит, найдется
многочлен p О PQ с r(p,F) < e/2. По шагу 1 функция
j(z) := gj0(z) + p(z) содержится в UQ(O) и
удовлетворяет оценке ![]() = 1, O № C - открытое множество с односвязными компонентами, причем
0 О O и содержащая 0 компонента является звездою
относительно точки 0. Тогда множество UQ(O) плотно в HQ(O).
= 1, O № C - открытое множество с односвязными компонентами, причем
0 О O и содержащая 0 компонента является звездою
относительно точки 0. Тогда множество UQ(O) плотно в HQ(O).