Армен А. Вагаршакян
О представлении функций пространства
ReH1
(Представлено
академиком А.А. Талаляном 8/XII 2004)
Пусть | ReH1 -
пространство, состоящее из граничных значений действительных частей функций
пространства Харди H1, определённого в верхней полуплоскости.
| ReH1 является банаховым пространством с нормой
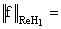 |
+Ґ
у
х
-Ґ
|
|f(x)|dx + |
+Ґ
у
х
-Ґ
|
|Hf(x)|dx, | |
где
через Hf(x) обозначено преобразование Гильберта функции f(x), т.е.
| Hf(x) = v.p. |
+Ґ
у
х
-Ґ
|
|
f(t)
x - t
|
dt. | |
Известно, что | ReH1 -
собственное подпространство L1(R). Данная статья посвящена задаче
представления функций | ReH1. Для формулировки основных результатов
приведём следующие определения.
Назовём функцию j,
принадлежащую пространству LҐ(R), атомом,
если существует интервал I такой, что
1.
| supp j М
I;
2.
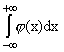 = 0; = 0; 3. ||j||Ґ Ј [1/(|I|)],
где через |I| обозначена длина интервала I.
Функция j,
удовлетворяющая следующему дополнительному условию
4.
|j(x)| = [1/(|I|)]
п.в., x О I,
будет называться специальным атомом.
Следующая теорема доказана Ч. Фефферманом
(см. [1]).
Теорема (Ч. Фефферман). Пространство | ReH1
совпадает с множеством функций,
допускающих представление
с дополнительным условием на
коэффициенты
где jk(x) - атомы, а ряд (1) сходится в пространстве
| ReH1.
При этом
где
inf берётся по всем разложениям вида (1), (2) функции f(x), а c и C (0 < c
< C < Ґ) - абсолютные постоянные.
Отметим, что первоначальное доказательство
этой теоремы достаточно сложно. Заметим, что, опираясь на неё, Ч. Фефферман
установил следующее равенство: ( | ReH1)* = BMO. Однако
существует независимое доказательство равенства ( | ReH1)* = BMO (см. [2], с. 241).
Используя этот факт, нам удаётся не только упростить доказательство теоремы о
представлении, но и наложить дополнительные ограничения на атомы. Основной
результат данной статьи сформулирован в следующей теореме.
Теорема 1. Пространство
| ReH1 совпадает с множеством функций,
допускающих представление
с дополнительным условием на коэффициенты
где
jk(x) - специальные атомы.
Естественно возникает вопрос: насколько можно
сузить множество атомов, участвующих в представлении пространства | ReH1? Было бы желательно, чтобы атомы,
участвующие в представлении, рождались сдвигами и сжатиями одной "материнской"
функции, подобно всплескам. Однако, как показывает следующая теорема, это
невозможно.
Теорема 2. Пусть
| lk >
l0 > 0,
xk О R,
k = 1,2,ј | |
некоторые
числовые последовательности. Тогда для любой функции j
О | ReH1 существует
f О | ReH1, которую
невозможно представить в виде ряда
| f(x) = |
+Ґ
е
k=1
|
ck · lkj(lk(x - xk)), | |
где коэффициенты абсолютно сходятся, т. е.
Ереванский государственный
университет
Литература
1. Fefferman Ch. - Bull. Amer. Math. Soc. 1971. V.77. P
104-112.
2. Garnett J.
Bounded Analytic Functions. Academic Press. 1981.
| 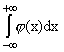 = 0;
= 0;