МАТЕМАТИКА
УДК 517.53
А. М. Джрбашян
О функциях w-ограниченного вида в
полуплоскости
(Представлено академиком В.С. Закаряном 30/IX
2004)
Введение. Общеизвестно,
что в задачах, относящихся к классам функций, регулярных в полуплоскости
конечной комплексной плоскости, естественны ограничения на рост функций,
инвариантные относительно паралельного сдвига, а также аппарат преобразований
Фурье - Лапласа. Такие ограничения на рост рассматривают конечные граничные
точки равносильно, а Ґ - иначе. С другой стороны, в
работе [1] показано, что инвариантное относительно сдвига условие естественно
дополнять локальным условием в окрестности Ґ. Именно
таким образом введены исследуемые в данной статье классы регулярных в
полуплоскости функций.
В статье даны представления общей теории
функций w-ограниченного вида в верхней полуплоскости.
Получены канонические представления некоторых банаховых пространств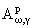 голоморфных функций. При p = 2 (т.е. в гильбертовом случае) установлены: теорема
об ортогональной проекции из
голоморфных функций. При p = 2 (т.е. в гильбертовом случае) установлены: теорема
об ортогональной проекции из
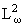 в
в
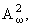 теорема типа Пэли - Винера
и теорема о естественнй изометрии
теорема типа Пэли - Винера
и теорема о естественнй изометрии
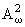 с пространством Харди H2, являющейся
интегральным оператором вместе со своим обратным. Затем даны канонические
представления d-субгармонических классов типа
Неванлинны - Джрбашяна. Рассматриваемые функции могут иметь любой рост вблизи
конечных точек вещественной оси.
с пространством Харди H2, являющейся
интегральным оператором вместе со своим обратным. Затем даны канонические
представления d-субгармонических классов типа
Неванлинны - Джрбашяна. Рассматриваемые функции могут иметь любой рост вблизи
конечных точек вещественной оси.
1. Пространства
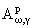 . Определим
. Определим
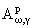 (0 < p < +Ґ, -Ґ <
g Ј 2) как множество тех
функций f(z) голоморфных в верхней полуплоскости G+ = {z : Im z > 0},
которые при достаточно малых r > 0 удовлетворяют
неванлинновскому условию
(0 < p < +Ґ, -Ґ <
g Ј 2) как множество тех
функций f(z) голоморфных в верхней полуплоскости G+ = {z : Im z > 0},
которые при достаточно малых r > 0 удовлетворяют
неванлинновскому условию
|
lim inf
R®+Ґ
|
|
1
R
|
|
у
х |
p-b
b
|
log+|f(ReiJ)| |
ж
з
и |
sin |
p(J - b)
p - 2b
|
ц
ч
ш |
1-p/k
|
dJ =
0, | |
(1.1) |
где b =
arcsin[(r)/R] = [(p)/2] - k и, одновременно,
| ||f||pp,w,g є |
у
х |
у
х |
G+
|
|f(z)|p |
dmw(z)
(1 + |z|)g
|
< +Ґ, | |
(1.2) |
где dmw(x + iy) = dxdw(2y) и w(t) О Wa (a і -1), т.е. w(t) в [0,+Ґ) таково, что
(i) w(t)
& (не убывает) в (0,+Ґ), w(0)=w(+0) и существует последовательность dkЇ0 такая, что w(dk)Ї (строго убывает),
(ii) w(t)  t1+a при
D0 Ј t <
+Ґ (D0 і 0)
t1+a при
D0 Ј t <
+Ґ (D0 і 0)
(f(t)
 g(t) означает, что m1f(t)
Ј g(t) Ј m2f(t) при
некоторых постоянных m1,2 > 0). Определим лебегово пространство
g(t) означает, что m1f(t)
Ј g(t) Ј m2f(t) при
некоторых постоянных m1,2 > 0). Определим лебегово пространство
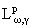 одним лишь условием (1.2) и отметим, что при w(t) О Wa (a і -1) ограничение (ii) имеет место
при любом D О (0,D0].
одним лишь условием (1.2) и отметим, что при w(t) О Wa (a і -1) ограничение (ii) имеет место
при любом D О (0,D0].
Замечание 1.1. Очевидно
 = (i + z)g/p
= (i + z)g/p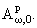 Далее, при w(t) = t1+a (a > -1), g = 0 и p і 1 пространство
Далее, при w(t) = t1+a (a > -1), g = 0 и p і 1 пространство
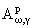 совпадает с хорошо известным
совпадает с хорошо известным
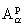 в полуплоскости (см. [2], [3], [4], а также [5]). В этом случае из (1.2) следует
(1.1), и эта импликация верна в более общем случае - когда w(t) непрерывно дифференцируемо в (0,+Ґ) и таково, что wў(t) і Mta (a > -1) для почти всех t > 0 и некоторой постоянной M > 0.
в полуплоскости (см. [2], [3], [4], а также [5]). В этом случае из (1.2) следует
(1.1), и эта импликация верна в более общем случае - когда w(t) непрерывно дифференцируемо в (0,+Ґ) и таково, что wў(t) і Mta (a > -1) для почти всех t > 0 и некоторой постоянной M > 0.
Замечание 1.2. В общем
случае (1.2) не обеспечивает выполнение условия (1.1). К необходимости наложения
условия (1.2) мы вернемся в конце раздела 3.
Напомним некоторые свойства [1] голоморфных
пространств Харди
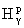 є
Hp є
Hp |
ж
з
и |
|
dx
(1 + |x|)g
|
|
ц
ч
ш |
= (z + i)g/p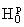 | |
(1.3) |
(0 < p < +Ґ, -Ґ <
g Ј 2), где
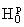 є Hp пространство
Харди, введенное в верхней полуплоскости G+ = {z : Im z > 0}
ограничением
є Hp пространство
Харди, введенное в верхней полуплоскости G+ = {z : Im z > 0}
ограничением
|
sup
y > 0
|
|
у
х |
+Ґ
-Ґ
|
|f(x + iy)|pdx < +Ґ. | |
(1.4) |
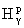 совпадает со множеством тех функций f(z), голоморфных
в G+, для которых |f(z)|p имеет гармоническую мажоранту в G+
(т.е. f(z) лежит в конформном образе пространства Харди Hp из |z| < 1) и f(x) О Lp([dx/((1+|x|)g )]) є
совпадает со множеством тех функций f(z), голоморфных
в G+, для которых |f(z)|p имеет гармоническую мажоранту в G+
(т.е. f(z) лежит в конформном образе пространства Харди Hp из |z| < 1) и f(x) О Lp([dx/((1+|x|)g )]) є
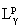 на
вещественной оси.
на
вещественной оси.
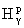 (1 Ј p < +Ґ, -Ґ < g
Ј 2) является Банаховым пространством с нормой
(1 Ј p < +Ґ, -Ґ < g
Ј 2) является Банаховым пространством с нормой
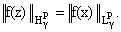 При этом
При этом
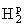 совпадает с
конформным образом Hp из |z| < 1, а при g = 0 - с
совпадает с
конформным образом Hp из |z| < 1, а при g = 0 - с
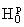 , определяемым условием (1.4). Кроме того, из
результатов [1] следует, что
, определяемым условием (1.4). Кроме того, из
результатов [1] следует, что
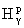 (0 < p < +Ґ, -Ґ < g Ј
2) совпадает со множеством тех голоморфных в G+ функций, которые
удовлетворяют (1.1) при любом r > 0 и таковы, что
(0 < p < +Ґ, -Ґ < g Ј
2) совпадает со множеством тех голоморфных в G+ функций, которые
удовлетворяют (1.1) при любом r > 0 и таковы, что
|
lim inf
y®+0
|
|
у
х |
+Ґ
-Ґ
|
|f(x + iy)|p |
dx
(1 + |x|)g
|
< +Ґ. | |
(1.5) |
В [1] ясно, что полуплоскость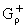 = {z : Im z > r} может быть исчерпана круговыми сегментами, а следовательно
при (1.2) условие (1.1) эквивалентно тому, что
= {z : Im z > r} может быть исчерпана круговыми сегментами, а следовательно
при (1.2) условие (1.1) эквивалентно тому, что
|
lim inf
R®+Ґ
|
|
1
R
|
|
у
х |
p-b
b
|
|f(ReiJ)|p |
ж
з
и |
sin |
p(J - b)
p - 2b
|
|
ц
ч
ш |
1-p/k
|
dJ < +Ґ | |
(1.1ў) |
при
любом r > 0, а также каждому из следующих двух
условий:
|
lim inf
R®+Ґ
|
|
1
R
|
|
у
х |
p
0
|
log|f(ReiJ + ir)|sinJdJ = 0, |
lim inf
R®+Ґ
|
|
1
R
|
|
у
х |
p
0
|
|f(ReiJ + ir)|psinJdJ < +Ґ. | |
Кроме
того, если f(z) О
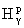 (-Ґ
< g Ј 2, 0 < p <
+Ґ), то при любом 0 < M < +Ґ
(-Ґ
< g Ј 2, 0 < p <
+Ґ), то при любом 0 < M < +Ґ
|
sup
0 < y < M
|
у
х |
+Ґ
-Ґ
|
|f(x + iy)|p |
dx
(1 + |x|)g
|
< +Ґ. | |
(1.6) |
Проверяя выполнение (1.6), легко
показать, что при любом p > 1
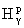 М М
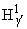 при при |
м
п
п
н
п
п
о
|
|
| |
(1.7) |
Отметим, что если f(z) О
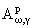 (p > 0, w О Wa, a і -1, -Ґ < g
< 1), то f(z + ir) принадлежит
(p > 0, w О Wa, a і -1, -Ґ < g
< 1), то f(z + ir) принадлежит
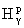 при любом r > 0. Кроме
того, верно следующее
при любом r > 0. Кроме
того, верно следующее
Предложение 1.1. При любых p > 0
и g О (-Ґ,2]
сумма ИwОWa
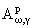 совпадает со множеством
всех функций, принадлежащих
совпадает со множеством
всех функций, принадлежащих
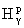 в
любой полуплоскости
в
любой полуплоскости
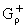 (r > 0).
(r > 0).
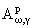 (1 Ј p < +Ґ, -Ґ <
g < 1, w О Wa, a і -1) является Банаховым
пространством с нормой (1.2).
(1 Ј p < +Ґ, -Ґ <
g < 1, w О Wa, a і -1) является Банаховым
пространством с нормой (1.2).
2. Представление по
полосе. Полагая, что w(t) О Wa (a і -1), будем пользоваться следующим
континуальным аналогом ядра типа Коши М.М.Джрбашяна:
| Cw(z) = |
у
х |
+Ґ
0
|
eitz |
dt
Iw(t)
|
, Iw(t) = |
у
х |
+Ґ
0
|
e-txdw(x). | |
(2.1) |
Функция Cw(z) голоморфна в G+, поскольку условия (i),
(ii) обеспечивают равномерную сходимость интеграла (2.1) внутри G+.
Отметим, что ядро (2.1) впервые было использовано А.О.Карапетяном [6], где оно
было построено в многомерном случае трубчатых областей (см. также [7-9]). В
случае простой шкалы w(t) = t1+a имеем Iw(t) = G(2 + a)t-(1+a) и Cw(z) = (-iz)-(2+a)
(-2 < a < +Ґ).
Для установления канонических представлений
пространств
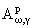 найден новый подход к применению преобразований Фурье
- Лапласа, отличающийся от известного подхода [10]. Существенны также включения
(1.7) и следующее утверждение о представимости интегралом Коши в
найден новый подход к применению преобразований Фурье
- Лапласа, отличающийся от известного подхода [10]. Существенны также включения
(1.7) и следующее утверждение о представимости интегралом Коши в
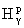 :
если f(z)
О
:
если f(z)
О
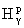 (p
і 1, g < 1), то
(p
і 1, g < 1), то
| f(z) = |
1
2pi
|
|
у
х |
+Ґ
-Ґ
|
|
f(t)
t - z
|
dt и |
1
2pi
|
|
у
х |
+Ґ
-Ґ
|
f(t)
t -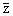 |
dt = 0 z О
G+. | |
Теорема 2.1. Пусть f(z) О
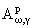 (G+)
при
некоторых 1 Ј p < +Ґ, -Ґ < g
< 1 и w(x) удовлетворяющем (i) и таком, что w(t) = w(D)
< +Ґ (D < t < +Ґ) при некотором D > 0. Тогда
(G+)
при
некоторых 1 Ј p < +Ґ, -Ґ < g
< 1 и w(x) удовлетворяющем (i) и таком, что w(t) = w(D)
< +Ґ (D < t < +Ґ) при некотором D > 0. Тогда
| f(z) = |
1
2p
|
|
у
х |
у
х |
G+
|
f(w)Cw(z -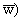 |
dmw(w), z О G+, | |
(2.2) |
| f(z) = |
1
p
|
|
у
х |
у
х |
G+
|
{Re f(w)}Cw(z -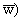 |
dmw(w), z О G+, | |
(2.3) |
где оба интеграла абсолютно и
равномерно сходятся внутри G+.
3. Представления по всей
полуплоскости. Устремление D ® +Ґ в (2.2) и (2.3), приводящее к
цели, основано на следующей лемме.
Лемма 3.1. Пусть w(x) О Wa при некотором a і -1.
Тогда для любого не целочисленного значения b О ([a] - 1,a) и любого r > 0 существует положительная постоянная M є Mr,b такая, что
|Cw(z)| Ј M|z|-(2+b), z О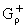 . . | |
Теорема 3.1. Пусть f(z) О
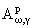 при некоторых 1 Ј p < +Ґ и -Ґ < g
< 1 - (1 + a)(p - 1). Тогда опять же справедливы представления (2.2)
и (2.2), где оба интеграла абсолютно и равномерно сходятся внутри G+.
при некоторых 1 Ј p < +Ґ и -Ґ < g
< 1 - (1 + a)(p - 1). Тогда опять же справедливы представления (2.2)
и (2.2), где оба интеграла абсолютно и равномерно сходятся внутри G+.
Замечание 3.1. В случае,
когда 1 Ј p Ј 2 и мера dw абсолютно непрерывна, представление (2.2) было установлено
в [6-9] для общих, весовых классов со смешанной нормой в радиальных трубчатых
областях из Cn.
Справедливо следующее утверждение о проекции
из
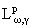 в
в
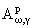 .
.
Теорема 3.2. Пусть f(z) О
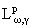 (1 Ј p < +Ґ, -Ґ < g
< 1) и пусть w(x) таково, как в теоремах 2.1 или
3.1. Тогда интегралы в формулах (2.2) и (2.3) представляют голоморфные в
G+ функции, для которых верно (1.1).
(1 Ј p < +Ґ, -Ґ < g
< 1) и пусть w(x) таково, как в теоремах 2.1 или
3.1. Тогда интегралы в формулах (2.2) и (2.3) представляют голоморфные в
G+ функции, для которых верно (1.1).
Замечание 3.2. Ввиду
последней теоремы представления (2.2) и (2.3) могут быть использованы вместе с
оценкой ядра [11] для установления теорем о проекции из
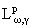 в
в
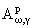 и описания сопряженного
пространства
и описания сопряженного
пространства
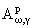 - так, как это сделано в [12,13] - в круге.
- так, как это сделано в [12,13] - в круге.
4. Ортогональная прекция и
изометрия. Верна следующая
Теорема 4.1. Оператор ортогональной проекции пространства
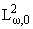 на свое подпространство
на свое подпространство
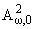 (w О Wa, a і -1, w(0) = 0) записывается в виде
(w О Wa, a і -1, w(0) = 0) записывается в виде
| Pw
f(z) = |
1
2p
|
|
у
х |
у
х |
G+
|
f(w)Cw(z -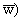 |
dmw(w), f О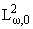 . . | |
Следующее утверждение является аналогом
теоремы Пэли - Винера.
Теорема 4.2. Пространство
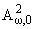 (w О Wa, a і -1,
w(0) = 0) совпадает со множеством всех функций,
представимых в виде
(w О Wa, a і -1,
w(0) = 0) совпадает со множеством всех функций,
представимых в виде
| f(z) = |
1
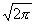 |
|
у
х |
+Ґ
0
|
eitz |
F(t)
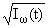 |
dt, z О G+, F(t) О
L2(0,+Ґ). | |
(4.1) |
Если такое
представление верно, то
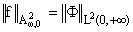 и
и
|
| F(t) = |
1
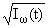 |
|
у
х
|
+Ґ
0
|
e-tv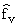 (t)dw(2v), (t)dw(2v), |
|
| где
|
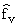 (t) = (t) = |
l.i.m.
R®+Ґ
|
|
1
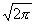 |
|
у
х
|
R
-R
|
e-ituf(u + iv)du. | | |
| |
(4.2) |
Замечание 4.1. В
частном случае абсолютно непрерывной меры dw теорема
4.2 следует из более общих утверждений [6], [14] в весовых пространствах со
смешанной нормой в трубчатых областях из Cn.
Замечание 4.2. В
дополнение к теореме 4.2 верно следующее утверждение: пусть
S1 - множество тех w(x), которые непрерывны
и при некотором D О (0,+Ґ) строго возрастают в [0,D], w(0) = 0 и w(x) = w(D) при x > D. Далее, пусть S2 - (более широкое) множество тех
w(x), w(0) = 0, которые
принадлежат Wa
при
каком-либо a і -1. Тогда
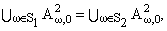 и обе
эти суммы совпадают со множеством всех функций вида
и обе
эти суммы совпадают со множеством всех функций вида
| f(z) = |
у
х |
+Ґ
0
|
eitzY(t)dt, z О G+, где e-etY(t) О
L2(0,+Ґ) при любом e
> 0. | |
Следующая теорема в частности дает больше
информации о функции F, участвующей в представлении
(4.1). Предварительно введем в рассмотрение оператор
| Lw f(z)
є |
у
х |
+Ґ
0
|
f(z + is)dw(s) | |
и
отметим, что: если w(x) О Wa (-1 Ј a < +Ґ) и w(0) = 0, то квадрат Вольтерра
функции w(x), т.е. функция
|
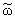 (x) = (x) = |
у
х |
x
0
|
w(x - t)dw(t), 0 < x < +Ґ, |
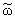 (0) = 0, (0) = 0, | |
(4.3) |
принадлежит W1+2a. Кроме того,
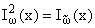 (0 < x < +Ґ).
(0 < x < +Ґ).
Теорема 4.3. Пусть функция w(t) (w(0) = 0) принадлежит Wa (-1 Ј a < +Ґ) и пусть
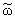 -
ее квадрат
Вольтерра (4.3). Тогда
-
ее квадрат
Вольтерра (4.3). Тогда
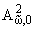 совпадает со множеством функций,
представимых в виде
совпадает со множеством функций,
представимых в виде
| f(z) = |
1
2p
|
|
у
х |
+Ґ
-Ґ
|
j(t)Cw(z - t)dt, z О G+, j О L2(-Ґ,+Ґ). | |
(4.4.) |
Если f О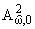 ,
то единственной
функцией из пространства Харди H2 є
,
то единственной
функцией из пространства Харди H2 є
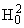 ,
которой можно заменить j(t)
в (4.4), является Lwf. Кроме того,
,
которой можно заменить j(t)
в (4.4), является Lwf. Кроме того,
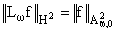 и j - Lwf ^ H2 для любой функции j
О L2(-Ґ,+Ґ),
с которой верно (4.4).
Оператор Lw является изометрией
и j - Lwf ^ H2 для любой функции j
О L2(-Ґ,+Ґ),
с которой верно (4.4).
Оператор Lw является изометрией
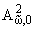 ® H2, а интеграл (4.4) определяет (Lw)-1 в
H2.
® H2, а интеграл (4.4) определяет (Lw)-1 в
H2.
Замечание 4.3. При
условиях теоремы 4.3 в представлении (4.1) пространства
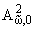 функция F является преобразованием Фурье функции Lw f по вещественной оси.
функция F является преобразованием Фурье функции Lw f по вещественной оси.
5. Весовые классы гармонических
функций. Справедлива следующая
Теорема 5.1. Пусть функция U(z)
гармонична в полуплоскости G+ и такова,
что для достаточно малых r > 0 и некотором g О (-Ґ,2]
|
lim inf
R®+Ґ
|
|
1
R
|
|
у
х |
p-b
b
|
|U(ReiJ)| |
ж
з
и |
sin |
p(J - b)
p - 2b
|
ц
ч
ш |
1-p/k
|
dJ =
0, | |
(5.1) |
|
у
х |
у
х |
G+
|
|U(z)| |
dmw(z)
(1 + |z|)g
|
< +Ґ, | |
(5.2) |
где b =
arcsin[(r)/R] = [(p)/2] - k и dmw(x + iy) = dxdw(2y). Далее, пусть выполнено одно из следующих условий:
1°. w(t) удовлетворяет условию (i)
(см. раздел 1) и w(t) = w(D) (D
< t < +Ґ) при некотором D > 0, или же
2°. w(t) О Wa при некоторых a і -1 и
g < 1.
Тогда
| U(z) = |
1
p
|
|
у
х |
у
х |
G+
|
U(w)Re {Cw(z -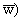 } } |
dmw(w), z О G+, | |
(5.3) |
где интеграл абсолютно и
равномерно сходится внутри G+.
Замечание 5.1. Для
классов гармонических в G+ функций, определенных условиями (5.1) и
(5.2) с заменой |U| на |U|p (1 Ј p < +Ґ), представление (5.3)
доказано также в случае, когда интеграл берется по полосе (т.е. w(t) = w(D),
D < t < +Ґ)
6. Классы типа Неванлинны -
Джрбашяна в полуплоскости. Всюду ниже будем полагать, что U(z) является
d-субгармоничнеской в G+ функцией и n - ее ассоциированная мера, т.е. U(z) = U1(z) - U2(z), где U1,2(z) субгармонические в
G+ функции с риссовскими ассоциированными мерами n1,2, и n = n1 + n2. Кроме
того, будем полагать, что мера n минимально разложена в
Жордановом смысле, т.е. n = n+ - n-, где (supp n+) З (supp n-) = Ж и n± - положительная и отрицательная вариации меры n. Будем говорить, что две d-субгармонические в какой-либо области G функции равны, т.е.
U(z) = V(z), где V(z) = V1(z) - V2(z)
(и V1,2(z) субгармоничны в G), если
U1(z) + V2(z) = U2(z) + V1(z) всюду в G.
Для d-субгармонической в G+ функции U(z)
будем рассматривать характеристику Цудзи следующего вида:
| L(y,U) є |
1
2p
|
|
у
х |
+Ґ
-Ґ
|
U+(x + iy)dx + |
у
х |
+Ґ
y
|
n+(t)dt, 0 <
y < +Ґ, | |
где
n+(t) =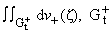 = {z : Im z > t}. Полагая характеристику L(y, -U) определенной аналогично -
посредством U- и n-, отметим, что в общем
случае L(y, U) либо L(y, -U), либо же обе эти величины могут быть бесконечны. Тем не
менее, существуют некоторые условия (см. [15], гл. 5), при которых
величины L(y, ±U) (0 < y <
+Ґ) конечны и связаны особой формой формулы Б.Я.
Левина:
= {z : Im z > t}. Полагая характеристику L(y, -U) определенной аналогично -
посредством U- и n-, отметим, что в общем
случае L(y, U) либо L(y, -U), либо же обе эти величины могут быть бесконечны. Тем не
менее, существуют некоторые условия (см. [15], гл. 5), при которых
величины L(y, ±U) (0 < y <
+Ґ) конечны и связаны особой формой формулы Б.Я.
Левина:
| L(y,U) = L(y, -U), 0
< y < +Ґ, | |
(6.1) |
что является естественным аналогом
хорошо известного соотношения равновесия для характеристик Неванлинны по
концентрическим кругам.
Определение 6.1.
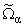 (a > -1) - множество функций w(x), w(0) = 0, которые непрерывны и строго возрастают в [0, +Ґ), непрерывно дифференцируемы в (0, +Ґ) и таковы, что wў(x)
(a > -1) - множество функций w(x), w(0) = 0, которые непрерывны и строго возрастают в [0, +Ґ), непрерывно дифференцируемы в (0, +Ґ) и таковы, что wў(x)
 xa (D < x < +Ґ) при любом D > 0.
xa (D < x < +Ґ) при любом D > 0.
Легко видеть, что если w(x) О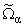 , то при любом
r і 0 функция w(x + r) принадлежит классу Wa, использованному
ранее.
, то при любом
r і 0 функция w(x + r) принадлежит классу Wa, использованному
ранее.
Нижеследующее определение аналога
неванлинновского весового класса в полуплоскости (см. п. 216 в [16], а также
[15]) естественно ввиду того, что в общем случае формула (6.1) не верна.
Определение 6.2. Nw (w(x) О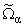 , a > -1) - множество d-субгармонических в G+ функций, для
которых
, a > -1) - множество d-субгармонических в G+ функций, для
которых
|
у
х |
+Ґ
0
|
[L(y,U) + L(y, -U)]dw(2y) < +Ґ. | |
(6.2) |
Формулировку теоремы о
каноническом представлении d-субгармонических функций
из классов
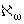 предварим
следующим утверждением.
предварим
следующим утверждением.
Теорема 6.1. Пусть w(x) О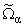 (-1 Ј a <
+Ґ). Тогда функция
(-1 Ј a <
+Ґ). Тогда функция
| bw(z,z) = exp |
м
н
о |
- |
у
х |
2Im z
0
|
Cw(z - z + it)w(t)dt |
ь
э
ю |
, Im z > Im z, | |
голоморфно
продолжается на все G+, где имеет единственный, простой нуль в точке
z = z. Если последовательность {zk} М G+ удовлетворяет условию
|
е
k
|
|
у
х |
2Imzk
0
|
w(t)dt < +Ґ, | |
то
внутри G+ сходится произведение типа Бляшке Bw(z,{zk}) є Хkbw(z,zk).
Теорема 6.2. Пусть U(z) О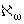 при некотором w(x) О
при некотором w(x) О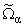 (a > -1). Тогда
(a > -1). Тогда
|
у
х |
у
х |
G+
|
|U(z)|dmw(z) < +Ґ, |
у
х |
у
х |
G+
|
|
ж
и |
у
х |
2Im z
0
|
w(t)dt |
ц
ш |
dn±(z) < +Ґ, | |
(6.3) |
и при любом r > 0
|
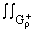 (1+Im z)dn±(z) < +Ґ. (1+Im z)dn±(z) < +Ґ. | |
Кроме
того, потенциалы типа Грина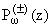 є ттG+log|bw(z,z)|dn±(z) по положительной и отрицательной вариациям асоциированной
меры функции U(z) сходятся, и в G+ имеет место представление
є ттG+log|bw(z,z)|dn±(z) по положительной и отрицательной вариациям асоциированной
меры функции U(z) сходятся, и в G+ имеет место представление
| U(z) = |
у
х |
у
х |
G+
|
log|bw(z,z)|dn(z) + |
1
p
|
|
у
х |
у
х |
G+
|
U(w)Re |
м
н
о |
Cw(z -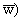 |
ь
э
ю |
dmw(w). | |
(6.4) |
В заключение приведем еще одну теорему, которая несколько
отличается от теоремы 6.1, а также некоторые замечания. Аналогично
разделу 2, можно рассматривать весовые классы d-субгармонических функций с гармоническими составляющими,
записываемыми в виде интегралов по полосе. А именно, верна следующая
Теорема 6.3. Пусть U(z) О
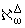 ,
где D > 0 - какое-либо фиксированное число и w(x), w(+0) = 0 - строго возрастающая
на (0,D) функция, такая что w(x) = w(x + D)
(0 < x < +Ґ). Тогда все утверждения теоремы 6.2
остаются в силе.
,
где D > 0 - какое-либо фиксированное число и w(x), w(+0) = 0 - строго возрастающая
на (0,D) функция, такая что w(x) = w(x + D)
(0 < x < +Ґ). Тогда все утверждения теоремы 6.2
остаются в силе.
Замечание 6.1. Пусть субгармоническая в G+
функция U(z) такова, что
|
у
х |
у
х |
G+
|
|U(z)|dmw(z) < +Ґ, где | |
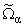 (-1 < a < +Ґ), или
(-1 < a < +Ґ), или
2°. w(x) строго
возрастающая в (0,D) (D >
0) функция такая, что w(+0) = 0 и w(x) = w(x + D) (0 < x < +Ґ) и, в добавок, U(z)
удовлетворяет (5.1).
Тогда U(z) принадлежит классу Nw (при выполнении 1°), или же
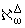 (при выполнении
2°). Тем самым, функция U(z) представима в
виде (6.4).
(при выполнении
2°). Тем самым, функция U(z) представима в
виде (6.4).
Замечание 6.2. В частном
случае, когда U(z) принадлежит
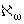 или же
или же
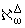 (w(x) таково, как в теоремах 6.2 или 6.3) и U(z) = log|f(z)| и f(z) мероморфная в
G+ функция, представление (6.4) переходит в
факторизацию вида
(w(x) таково, как в теоремах 6.2 или 6.3) и U(z) = log|f(z)| и f(z) мероморфная в
G+ функция, представление (6.4) переходит в
факторизацию вида
| f(z) = |
Bw(z,{an})
Bw(z,{bm})
|
exp |
м
н
о |
|
1
p
|
|
у
х |
у
х |
G+
|
log|f(w)|Cw(z -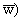 |
dmw(w) + iC |
ь
э
ю |
, z О
G+, | |
где C -
вещественное число, а {an}, {bm} М G+ - нули и полюсы f(z), которые удовлетворяют
(6.3).
В заключение отметим, что данная статья
дополняет результаты недавно вышедшей работы [17].
Институт математики НАН РА
Литература
1. Jerbashian A. M. - J. of Contemp. Math. Analysis. 1993. V. 28. N4. P.
42-61.
2. Coifman R. R., Rochberg
R. - Astérisque. 1980. V. 77. P.
12-67.
3. Ricci F., Taibleson M.
- Annali Scuola Normale Superiore - Pisa. Classe di Scienze.
Ser. IV. 1983. V. X. N1. P. 1-54.
4. Djrbashian M. M., Djrbashian A. E. - Dokl. Akad.
Nauk USSR. 1985. V. 285. N3. P. 547-550.
5. Djrbashian M. M., Karapetyan A. H. - Ann. Pol.
Math. 1991. V. 55. P. 87-94.
6. Карапетян А. О. Авторефер. канд. дис. Ереван.
1988.
7. Карапетян А. О.
- Изв. АН АрмССР. Математика. 1990. Т. 25. N4.
С. 315-332.
8. Карапетян А.
О. - Изв. АН АрмССР. Математика. 1991. Т. 26.
N1.
9. Карапетян А. О.
- Изв. АН АрмССР. Математика. 1992. Т. 27.
N1.
10. Гиндикин С. М.
- Успехи мат. наук. 1964. Т. 19. N4. С.
3-92.
11. Jerbashian A. M.
- Archives of Inequalities and Applications. 2003. V. 1.
P. 399-412.
12. Jerbashian
A. M. - Preprint 2002-01. Institute of Mathematics. National
Ac. of Sci. of Armenia. Yerevan. 2002.
13. Jerbashian A. M. - Complex Variables. 2005. V.
50. N3. P. 155-183.
14. Карапетян
А. О. - Изв. АН АрмССР. Математика. 1988. Т. 23. N1.
С. 91-96.
15. Jerbashian A.
M. - Springer Verlag. USA. 2005. 196
p.
16. Nevanlinna R. - Springer. Berlin. 1937.
17. Jerbashian A. M. In: Operator Theory: Advances and
applications. Birkhauser Verlay. Basel. 2005. V. 158. P. 141-158.
![]() t1+a при
D0 Ј t <
+Ґ (D0 і 0)
t1+a при
D0 Ј t <
+Ґ (D0 і 0)![]() g(t) означает, что m1f(t)
Ј g(t) Ј m2f(t) при
некоторых постоянных m1,2 > 0). Определим лебегово пространство
g(t) означает, что m1f(t)
Ј g(t) Ј m2f(t) при
некоторых постоянных m1,2 > 0). Определим лебегово пространство
![]() одним лишь условием (1.2) и отметим, что при w(t) О Wa (a і -1) ограничение (ii) имеет место
при любом D О (0,D0].
одним лишь условием (1.2) и отметим, что при w(t) О Wa (a і -1) ограничение (ii) имеет место
при любом D О (0,D0].![]() = (i + z)g/p
= (i + z)g/p![]() Далее, при w(t) = t1+a (a > -1), g = 0 и p і 1 пространство
Далее, при w(t) = t1+a (a > -1), g = 0 и p і 1 пространство
![]() совпадает с хорошо известным
совпадает с хорошо известным
![]() в полуплоскости (см. [2], [3], [4], а также [5]). В этом случае из (1.2) следует
(1.1), и эта импликация верна в более общем случае - когда w(t) непрерывно дифференцируемо в (0,+Ґ) и таково, что wў(t) і Mta (a > -1) для почти всех t > 0 и некоторой постоянной M > 0.
в полуплоскости (см. [2], [3], [4], а также [5]). В этом случае из (1.2) следует
(1.1), и эта импликация верна в более общем случае - когда w(t) непрерывно дифференцируемо в (0,+Ґ) и таково, что wў(t) і Mta (a > -1) для почти всех t > 0 и некоторой постоянной M > 0.
![]() є Hp пространство
Харди, введенное в верхней полуплоскости G+ = {z : Im z > 0}
ограничением
є Hp пространство
Харди, введенное в верхней полуплоскости G+ = {z : Im z > 0}
ограничением ![]() совпадает со множеством тех функций f(z), голоморфных
в G+, для которых |f(z)|p имеет гармоническую мажоранту в G+
(т.е. f(z) лежит в конформном образе пространства Харди Hp из |z| < 1) и f(x) О Lp([dx/((1+|x|)g )]) є
совпадает со множеством тех функций f(z), голоморфных
в G+, для которых |f(z)|p имеет гармоническую мажоранту в G+
(т.е. f(z) лежит в конформном образе пространства Харди Hp из |z| < 1) и f(x) О Lp([dx/((1+|x|)g )]) є
![]() на
вещественной оси.
на
вещественной оси.
![]() (1 Ј p < +Ґ, -Ґ < g
Ј 2) является Банаховым пространством с нормой
(1 Ј p < +Ґ, -Ґ < g
Ј 2) является Банаховым пространством с нормой
![]() При этом
При этом
![]() совпадает с
конформным образом Hp из |z| < 1, а при g = 0 - с
совпадает с
конформным образом Hp из |z| < 1, а при g = 0 - с
![]() , определяемым условием (1.4). Кроме того, из
результатов [1] следует, что
, определяемым условием (1.4). Кроме того, из
результатов [1] следует, что
![]() (0 < p < +Ґ, -Ґ < g Ј
2) совпадает со множеством тех голоморфных в G+ функций, которые
удовлетворяют (1.1) при любом r > 0 и таковы, что
(0 < p < +Ґ, -Ґ < g Ј
2) совпадает со множеством тех голоморфных в G+ функций, которые
удовлетворяют (1.1) при любом r > 0 и таковы, что
![]() = {z : Im z > r} может быть исчерпана круговыми сегментами, а следовательно
при (1.2) условие (1.1) эквивалентно тому, что
= {z : Im z > r} может быть исчерпана круговыми сегментами, а следовательно
при (1.2) условие (1.1) эквивалентно тому, что ![]() (p > 0, w О Wa, a і -1, -Ґ < g
< 1), то f(z + ir) принадлежит
(p > 0, w О Wa, a і -1, -Ґ < g
< 1), то f(z + ir) принадлежит
![]() при любом r > 0. Кроме
того, верно следующее
при любом r > 0. Кроме
того, верно следующее ![]() совпадает со множеством
всех функций, принадлежащих
совпадает со множеством
всех функций, принадлежащих
![]() в
любой полуплоскости
в
любой полуплоскости
![]() (r > 0).
(r > 0).
![]() (1 Ј p < +Ґ, -Ґ <
g < 1, w О Wa, a і -1) является Банаховым
пространством с нормой (1.2).
(1 Ј p < +Ґ, -Ґ <
g < 1, w О Wa, a і -1) является Банаховым
пространством с нормой (1.2).![]() найден новый подход к применению преобразований Фурье
- Лапласа, отличающийся от известного подхода [10]. Существенны также включения
(1.7) и следующее утверждение о представимости интегралом Коши в
найден новый подход к применению преобразований Фурье
- Лапласа, отличающийся от известного подхода [10]. Существенны также включения
(1.7) и следующее утверждение о представимости интегралом Коши в
![]() :
если f(z)
О
:
если f(z)
О
![]() (p
і 1, g < 1), то
(p
і 1, g < 1), то ![]()
![]() (G+)
при
некоторых 1 Ј p < +Ґ, -Ґ < g
< 1 и w(x) удовлетворяющем (i) и таком, что w(t) = w(D)
< +Ґ (D < t < +Ґ) при некотором D > 0. Тогда
(G+)
при
некоторых 1 Ј p < +Ґ, -Ґ < g
< 1 и w(x) удовлетворяющем (i) и таком, что w(t) = w(D)
< +Ґ (D < t < +Ґ) при некотором D > 0. Тогда ![]()
![]()
![]() .
.![]() при некоторых 1 Ј p < +Ґ и -Ґ < g
< 1 - (1 + a)(p - 1). Тогда опять же справедливы представления (2.2)
и (2.2), где оба интеграла абсолютно и равномерно сходятся внутри G+.
при некоторых 1 Ј p < +Ґ и -Ґ < g
< 1 - (1 + a)(p - 1). Тогда опять же справедливы представления (2.2)
и (2.2), где оба интеграла абсолютно и равномерно сходятся внутри G+.![]() в
в
![]() .
.![]() (1 Ј p < +Ґ, -Ґ < g
< 1) и пусть w(x) таково, как в теоремах 2.1 или
3.1. Тогда интегралы в формулах (2.2) и (2.3) представляют голоморфные в
G+ функции, для которых верно (1.1).
(1 Ј p < +Ґ, -Ґ < g
< 1) и пусть w(x) таково, как в теоремах 2.1 или
3.1. Тогда интегралы в формулах (2.2) и (2.3) представляют голоморфные в
G+ функции, для которых верно (1.1).![]() в
в
![]() и описания сопряженного
пространства
и описания сопряженного
пространства
![]() - так, как это сделано в [12,13] - в круге.
- так, как это сделано в [12,13] - в круге.![]() на свое подпространство
на свое подпространство
![]() (w О Wa, a і -1, w(0) = 0) записывается в виде
(w О Wa, a і -1, w(0) = 0) записывается в виде ![]()
![]() .
.![]() (w О Wa, a і -1,
w(0) = 0) совпадает со множеством всех функций,
представимых в виде
(w О Wa, a і -1,
w(0) = 0) совпадает со множеством всех функций,
представимых в виде ![]()
![]()
![]() и
и ![]()
![]() (t)dw(2v),
(t)dw(2v),![]() (t) =
(t) =![]()
![]() и обе
эти суммы совпадают со множеством всех функций вида
и обе
эти суммы совпадают со множеством всех функций вида ![]() (x) =
(x) =![]() (0) = 0,
(0) = 0,![]() (0 < x < +Ґ).
(0 < x < +Ґ). ![]() -
ее квадрат
Вольтерра (4.3). Тогда
-
ее квадрат
Вольтерра (4.3). Тогда
![]() совпадает со множеством функций,
представимых в виде
совпадает со множеством функций,
представимых в виде ![]() ,
то единственной
функцией из пространства Харди H2 є
,
то единственной
функцией из пространства Харди H2 є
![]() ,
которой можно заменить j(t)
в (4.4), является Lwf. Кроме того,
,
которой можно заменить j(t)
в (4.4), является Lwf. Кроме того,
![]() и j - Lwf ^ H2 для любой функции j
О L2(-Ґ,+Ґ),
с которой верно (4.4).
Оператор Lw является изометрией
и j - Lwf ^ H2 для любой функции j
О L2(-Ґ,+Ґ),
с которой верно (4.4).
Оператор Lw является изометрией
![]() ® H2, а интеграл (4.4) определяет (Lw)-1 в
H2.
® H2, а интеграл (4.4) определяет (Lw)-1 в
H2. ![]() функция F является преобразованием Фурье функции Lw f по вещественной оси.
функция F является преобразованием Фурье функции Lw f по вещественной оси. ![]() }
}![]() = {z : Im z > t}. Полагая характеристику L(y, -U) определенной аналогично -
посредством U- и n-, отметим, что в общем
случае L(y, U) либо L(y, -U), либо же обе эти величины могут быть бесконечны. Тем не
менее, существуют некоторые условия (см. [15], гл. 5), при которых
величины L(y, ±U) (0 < y <
+Ґ) конечны и связаны особой формой формулы Б.Я.
Левина:
= {z : Im z > t}. Полагая характеристику L(y, -U) определенной аналогично -
посредством U- и n-, отметим, что в общем
случае L(y, U) либо L(y, -U), либо же обе эти величины могут быть бесконечны. Тем не
менее, существуют некоторые условия (см. [15], гл. 5), при которых
величины L(y, ±U) (0 < y <
+Ґ) конечны и связаны особой формой формулы Б.Я.
Левина: ![]() (a > -1) - множество функций w(x), w(0) = 0, которые непрерывны и строго возрастают в [0, +Ґ), непрерывно дифференцируемы в (0, +Ґ) и таковы, что wў(x)
(a > -1) - множество функций w(x), w(0) = 0, которые непрерывны и строго возрастают в [0, +Ґ), непрерывно дифференцируемы в (0, +Ґ) и таковы, что wў(x)
![]() xa (D < x < +Ґ) при любом D > 0.
xa (D < x < +Ґ) при любом D > 0. ![]() , то при любом
r і 0 функция w(x + r) принадлежит классу Wa, использованному
ранее.
, то при любом
r і 0 функция w(x + r) принадлежит классу Wa, использованному
ранее. ![]() , a > -1) - множество d-субгармонических в G+ функций, для
которых
, a > -1) - множество d-субгармонических в G+ функций, для
которых ![]() предварим
следующим утверждением.
предварим
следующим утверждением. ![]() (-1 Ј a <
+Ґ). Тогда функция
(-1 Ј a <
+Ґ). Тогда функция ![]() при некотором w(x) О
при некотором w(x) О![]() (a > -1). Тогда
(a > -1). Тогда ![]() (1+Im z)dn±(z) < +Ґ.
(1+Im z)dn±(z) < +Ґ.![]() є ттG+log|bw(z,z)|dn±(z) по положительной и отрицательной вариациям асоциированной
меры функции U(z) сходятся, и в G+ имеет место представление
є ттG+log|bw(z,z)|dn±(z) по положительной и отрицательной вариациям асоциированной
меры функции U(z) сходятся, и в G+ имеет место представление
![]()
![]() ,
где D > 0 - какое-либо фиксированное число и w(x), w(+0) = 0 - строго возрастающая
на (0,D) функция, такая что w(x) = w(x + D)
(0 < x < +Ґ). Тогда все утверждения теоремы 6.2
остаются в силе.
,
где D > 0 - какое-либо фиксированное число и w(x), w(+0) = 0 - строго возрастающая
на (0,D) функция, такая что w(x) = w(x + D)
(0 < x < +Ґ). Тогда все утверждения теоремы 6.2
остаются в силе. ![]() (при выполнении
2°). Тем самым, функция U(z) представима в
виде (6.4).
(при выполнении
2°). Тем самым, функция U(z) представима в
виде (6.4). ![]() или же
или же
![]() (w(x) таково, как в теоремах 6.2 или 6.3) и U(z) = log|f(z)| и f(z) мероморфная в
G+ функция, представление (6.4) переходит в
факторизацию вида
(w(x) таково, как в теоремах 6.2 или 6.3) и U(z) = log|f(z)| и f(z) мероморфная в
G+ функция, представление (6.4) переходит в
факторизацию вида ![]()