|
(1.1) |
где относительно функции f(e) принимается, что f(0) = 0, f(e)
имеет два экстремума - максимум при eB+ >
0 и минимум при eB-
< 0, после которых сопротивляемость материала резко падает. В области e О [en-; en+] связь между s и
e практически линейная:
|
(1.2) |
где E - модуль Юнга, en+ = -en- пределы
пропорциональности при растяжении и сжатии. Для тел из хрупких материалов или
материалов с небольшой площадкой пластичности при непрерывном нагружении можно
предполагать, что функция f(e) обеспечивает
взаимно-однозначную связь между напряжениями и деформациями на отрезке [eB-; eB+]. Отметим, что в разложении функции f(e) в степенной ряд четные члены разложения обеспечивают
разносопротивляемость материала к растяжению и сжатию (B № 0 в (1.3)) и достижение максимума и минимума в различных
(eB+, sB+) и (eB-, sB-) точках. Здесь u(x), w(x) - продольное и нормальное
перемещения точек оси балки для напряжения s согласно
(1.3)-(1.7) получается где штрихом обозначено производное
по x, s - площадь, I = bh3/12 - момент инерции поперечного сечения
(b×h) балки, J = bh5/80. где
sn - предел пропорциональности материала,
причем sn+ = -sn- = sn, Mon - допускаемое для линейной
задачи значение изгибающего момента M0. В этом случае материал одинаково
сопротивляется растяжению и сжатию и функция (3.1) принимает экстремальные
значения при Здесь, согласно (2.3), принимая
M0 = aMon = 2aIsn/h, уравнение для
определения f1 = hwўў
представляется в виде где коэффициент a показывает увеличение несущей способности балки вследствие
учета нелинейности и допущения работы балки для напряжений s О [sn;sB]. В этом случае материал по-разному
сопротивляется растяжению и сжатию, а влиянием нелинейности более высокого
(кубического) порядка пренебрегается. Функция (4.1) имеет единственный экстремум
(максимум) в точке
При (4.7) из условия eB+ = f2 - [1/2]f1 = 2[(sB+)/E] получается предельное значение a в зоне растяжений которое показывает увеличение
несущей способности по сравнению с линейной задачей в зоне растяжения. Таким образом, при sB-/sB+ О [1;2] активным
является ограничение на деформации сжатия, а при sB-/sB+ = 2 ограничения на деформации растяжения и
сжатия дают одинаковые значения для несущей способности
Ниже, по формуле (4.13) для некоторых
значений sB-/sB+ и соответствующих a
приводятся значения z/h: где eB+, eB- - предельные значения деформаций растяжения и сжатия
определяются формулами (1.4). Подстановкой (5.1) в первое уравнение системы
(1.12) для определения параметров нагрузки для растяжения и сжатия a+, a- получаются формулы В заключение отметим, что в рассмотренной
нелинейной постановке решение даже для простейшей задачи изгиба балки связано с
определенными трудностями. Подход к решению задач изгиба упругих балок из
материалов, по-разному сопротивляющихся растяжению и сжатию, можно найти в [1],
где рассматриваются два варианта аппроксимации графика зависимости деформация -
напряжение - билинейный закон упругости и с двумя степенными законами. Институт механики НАН РА
1. Тимошенко С. Р. Курс сопротивления материалов. М.- Л. Гостехиздат. 1931. 571
с.
и из условий
s = Ee - Be2 - Ce3 (1.3)
max
s = sB+ = EeB+ - ![]() -
-![]() ,
,
получается
min
s = sB- = EeB- -
![]() -
-![]()
eB+ =
B
3C
ж
и
Ц
1+d
- 1
ц
ш , eB- =-
B
3C
ж
и
Ц
1+d
+ 1
ц
ш , d =
3CE
B2, (1.4)
Если для материала заданы E, sB+, sB-, то из (1.5) можно определить коэффициенты B и C
sB+ =
EB
9C
й
к
л
2
Ц
1+d
ж
з
и
1+
1
dц
ч
ш
-
2
d- 3
щ
ъ
ы
,
sB- = -
EB
9C
й
к
л
2
Ц
1+d
ж
з
и
1+
1
dц
ч
ш
+
2
d+ 3
щ
ъ
ы
.
(1.5)
где g =
B =
4E2
3(sB- + sB+)
g3
(g2 - 1)2, C =
16E3
27(sB- + sB+)2
g6
(g2 - 1)3, (1.6) ![]() > 1 корень
кубического уравнения
> 1 корень
кубического уравнения
g3 - 1,5ag2 + 0,5a = 0
ж
з
и a =
sB- + sB+
sB- - sB+ц
ч
ш .
e = uў - zwўў. (1.7)
откуда для продольного усилия T и
изгибающего момента M получаются формулы
s =
Euў - B(uў)2 - C(uў)3 - z[E - 2Buў - 3C(uў)2]wўў -
- z2(B + 3Cuў)(wўў)2 + z3(wўў)3,
(1.8)
T = Esuў - Bs(uў)2 - Cs(uў)3 - BI(wўў)2 - 3CIuў(wўў)2,
M = -EIwўў + (2B + 3Cuў)Iuўwўў + CJ(wўў)3, (1.9)
Tў = 0, M = M0.
(1.10)
Из (1.9)-(1.11) для определения перемещений
u,w получается система уравнений
u = 0, w = 0, M = M0 при
x = 0,
T = 0, w = 0, M = M0 при x = l.
(1.11)
где введены обозначения
Cf13 -
20
3(E - 2Bf2 - 3Cf22)f1 =
80M0
bh2,
Cf23 + Bf22 - Ef2 +
C
4f12f2 +
B
12f12 = 0, (1.12)
откуда в силу (1.11)
f1 = hwўў,
f2 = uў, (1.13)
Ниже рассматриваются некоторые частные случаи
закона упругости (1.3).
w =
x(x - l)
2hf1,
u = xf2. (1.14)
2. Пусть B = C = 0 (линейная задача). В этом
случае s = Ee из системы
(1.12) получается
f1 = hwўў = -
M0h
EI,
f2 = 0, (2.1)
откуда
u = 0, e = -zwўў,
s = -zEwўў, (2.2)
s = -z
M0
I,
max
(z) s = -
min
(z) s =
M0h
2I= sn,
Mon =
2Isn
h,
s = Ee - Ce3, (3.1)
откуда
eB = ±
![]() и max s = - min s =
и max s = - min s =![]() = sB,
= sB,(3.2)
Отметим, что формулы (3.2) получаются из
(1.4), (1.5) при B = 0.
C =
4
27
E3
sB2. (3.3)
Система уравнений (1.12) представляется в
виде
или с учетом
(1.13) и (3.3)
Cf13 -
20
3Ef1 =
80M0
bh2,
f2 = 0,
f2 = uў = 0,
f13 - 45
sB2
E2f1 - 540
sB2
E3bh2M0 = 0. (3.4)
f13 - 45
sB2
E2f1 - 90a
sB2sn
E3= 0, (3.5)
Подстановкой предельного значения
f1 из (3.6) в уравнение (3.5) для коэффициента a получается
eB = -
h
2wўў = -
1
2f1
=
![]()
, f1 = -3
sB
E. (3.6)
и увеличение несущей способности
балки очевидно.
4. Пусть B № 0,
C = 0 тогда
a = 1,2
sB
sn (sB > sn), (3.7)
s = Ee - Be2. (4.1)
откуда
eB+ =
E
2B и
max
s =
E2
4B= sB+, (4.2)
Из третьего соотношения (4.3) при s = -sB- для eB- получается
B =
E2
4sB+, eB+ = 2
sB+
E s
= E
ж
з
и 1 -
E
4sB+e
ц
ч
ш e. (4.3)
В рассматриваемом случае из системы уравнений
(1.12) для f1 = hwўў,
f2 = uў получается
eB- = -2
sB-
Eж
з
и
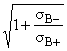
- 1
ц
ч
ш
. (4.4)
Подстановкой в (4.5) значения B из (4.3) и
M0 = 2aIsn/h получается система
f1 - 2
B
Ef2f1 = -
h
EIM0,
f22 -
E
Bf2 +
1
12f12 = 0. (4.5)
решение которой суть
f1 -
E
42sB+f2f1 + 2a1
sB+
E= 0
ж
з
и
a1=
sn
sB+a
ц
ч
ш
,
f22 -
4sB+1
Ef2 +
1
12f12 = 0, (4.6)
f1 = -
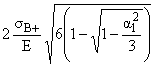 , f2
=
, f2
=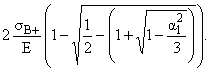
(4.7)
a+ = 1,5
sB+
sn (sB+ > sn), (4.8)
откуда для a получается
eB- = f2 +
1
2f1 = -2
sB+
Eж
з
и
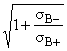
- 1
ц
ч
ш
, (4.9)
Как показывают расчеты,
a- =
3sB+
4sn
ж
з
и
sB-
sB+- 1
ц
ч
ш +
ж
ъ
Ц
3
4
й
к
л
1 -
1
4
ж
з
и
sB-
sB+- 1
ц
ч
ш
2
щ
ъ
ы
. (4.10)
0,866
sB+
snЈ a- Ј
sB+
sn
при
1 Ј
sB-
sB+Ј
1,185,
sB+
snЈ a- Ј
1,5
sB+
sn
при
1,185 Ј
sB-
sB+Ј
2,
1,5
sB+
snЈ a- Ј
Ц3
sB+
sn
при
2 Ј
sB-
sB+Ј
3. (4.11)
При sB-/sB+ > 2
активным является ограничение на деформации растяжения и a = 1,5sB+/sn.
a+ = a- = 1,5
sB+
sn.
Представляет интерес нахождение
нейтральной оси балки (s =
0 Ю e = 0).
Для деформации e =
f2 - [z/h]f1 по формулам (4.7)
получается
и из условия e = 0
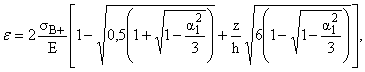
(4.12)
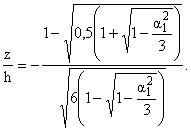
(4.13)
5. Рассмотрим теперь более общий случай
закона упругости (1.3)
sB-/sB+ = 1
(a =
0,866sB+/sn),
z/h = -0,038,
sB-/sB+ = 1,18
(a =
sB+/sn),
z/h = -0,045,
sB-/sB+ = 2
(a =
1,5sB+/sn),
z/h = -0,077,
sB-/sB+ = 3
(a = ![]() sB+/sn),
sB+/sn),
z/h = -0,12. (4.14)
Согласно (1.7), (1.13)
s = Ee - Be2 - Ce3.
откуда
при z = ±0,5h
f2 = e -
z
hf1,
f2+ = eB+ +
1
2f1,
f2- = eB- -
1
2f1, (5.1)
где f1+, f1
соответственно определяются из уравнений
a+ =
9C
20sn
ж
з
и f1+ +
10B
9Cg
ц
ч
ш
![]() , a- =
, a- =9C
20sn
ж
з
и f1- +
10B
9Cg
ц
ч
ш
![]() ,
,(5.2)
Здесь min(a+, a-) определяет параметр несущей способности балки.
![]() +
+![]() g
g![]() -
-![]() = 0,
= 0,
![]() +
+![]() g
g![]() -
-![]() =
0.
=
0.(5.3)
Из уравнений (5.1)-(5.3), при (1.4), (1.6),
для определения a+, a- получаются уравнения
где
![]() - (5,4 - K±)
- (5,4 - K±)![]() + (9,72 - 3K±)a1± -
+ (9,72 - 3K±)a1± -ж
з
и 5,832 -
9K±
4ц
ч
ш = 0, (5.4)
Для балки из боропластика с характеристиками
s-/sB+ = 2, E/sB+ = 150, E = 20,6 · 1010 Па получается
a1+ =
sn
sB+a+, a1- =
sn
sB-a-,
K+ =
8B3g3
45sB+C2, K- =
8B3g3
45sB-C2.
min
(a+,a-) = a+ = 1,35
sB+
sB-.
2. Амбарцумян С. А.
Разномодульная теория упругости. М. Наука. 1982.
317 с.
3. Амбарцумян С. А.
Сопротивление материалов, разносопротивляющихся растяжению и
сжатию. Ереван. Изд. РАУ. 2004. 187 с.