ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
УДК 517.58, 519.65
Академик А. Б. Нерсесян
Ускорение сходимости рядов Фурье-Бесселя
для
кусочно-гладких функций
(Представлено 27/XII 2004)
1. Общеизвестна роль
рядов Фурье-Бесселя как в теоретических, так и в прикладных исследованиях.
Известен также ряд критериев разложений функций в такие ряды (см., например,
[1,2]). Найден аналог известного в теории рядов Фурье s-фактора Ланцоша, несколько компенсирующего величину этого
явления (см.[3]). Однако в наиболее применимом случае,-а именно, когда
разлагаемая функция кусочно-гладкая и ряд сходится медленно,-нет эффективных
алгоритмов для ускорения сходимости. Здесь отметим работу [4], в которой
показано, что для гладкой на отрезке и быстро убываюшей на его концах функции
сходимость ряда Фурье-Бесселя ускоряется.
Между тем для классического ряда Фурье
имеется обширная литература, посвященная применениям многочленов Бернулли для
эффективного ускорения сходимости на основе идеи, предложенной А.Крыловым еще в
1933 г. [5] и практически развитого после 1990 г. в работах К.Экгофа, Д.Готтлиба
и др. (см. [6,7] и [8] с библиографией). Такой подход будем называть
КЭГ-методом.
С другой стороны, в работе [8] был разработан
нелинейный метод ускорения сходимости рядов Фурье, основанный на применении
аппроксимантов Паде, что привело к еще более точным и устойчивым алгоритмам,
позволяющим, к тому же, эффективно выявлять колебания произвольной частоты (в
том числе затухающие или нарастающие), являющиеся "скрытыми" компонентами
разлагаемой на конечном отрезке функции.
Ниже эти подходы распространяются на
разложения Фурье-Бесселя(см. [1])
|
|
|
| f(x) @ |
Ґ
е
n=1
|
fn Jn(jn x), n і -1/2, 0 Ј x Ј 1,
| |
(1) | |
где
{jn}-положительные корни уравнения Jn(z) = 0, пронумерованные в порядке возрастания, и
| fn = |
2
Jn+1(jn)2
|
|
у
х |
1
0
|
Jn(jn
t) t f(t) dt, n = 1,2,... | |
(2) | |
Ряд (1) сходится в весовом пространстве
L2([0,1],x) (т.е. при т01x|f(x)|2 dx < Ґ).
2. Предположим, что
x0 = 0 < x1 < .. < xl = 1, q і 1, f(x) О
C2q[xk-1,xk],
k = 2,...,l, f(x) О C2q[e,x1] при любом e, 0 <
e < x1 и введем в рассмотрение оператор
| Ln · = |
ж
з
и
|
- |
1
x
|
|
d
dx
|
x |
d
dx
|
+ |
n2
x2
|
ц
ч
ш
|
· , x > 0.
| |
(3) | |
Имеем (см.[2], глава 7) Ln ( Jn(j x)) = j2 Jn(j x), j > 0. В окрестности точки x О (0,1), x П {xk},
многократным интегрированием по частям получим (Ln0-единичный оператор)
|
|
|
|
у
х |
Jn(j x) x f(x) dx = j-2q |
у
х |
Lnq(f(x)) x Jn(j x) dx +
| |
|
|
|
| + x |
ж
и |
Jn(j x) |
q-1
е
r=0
|
j-2r-2 (Lnrf(x))ў-
Jn ў(j x) |
q-1
е
r=0
|
j-2r-1 (Lnrf(x)) |
ц
ш |
. | |
(4) | |
Предположим теперь, что (n x d / dx (Lnrf(x)) - Lnrf(x)) ®
0, x ® 0 при r = 0,1,...,(q - 1) и
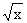 Lnqf(x)) О
L2(0,x1) . Отсюда и из (4), учитывая поведение
Jn(x) при x ® 0
(см.[1,2]), придем к асимптотическому разложению вида fn = Ynq + Rn q по
степеням jn-1 с точностью до
Rnq = o(n-2q), n ® Ґ, где
Lnqf(x)) О
L2(0,x1) . Отсюда и из (4), учитывая поведение
Jn(x) при x ® 0
(см.[1,2]), придем к асимптотическому разложению вида fn = Ynq + Rn q по
степеням jn-1 с точностью до
Rnq = o(n-2q), n ® Ґ, где
| Ynq = |
2
Jn+1(jn)2
|
|
l
е
k=1
|
xk |
ж
и |
Jn(jnxk) |
q
е
r=1
|
jn-2r A1rk - Jnў(jnxk) |
q
е
r=1
|
jn-2r+1 A0rk
|
ц
ш |
, | |
| Rn q = |
2
jn2q Jn+1(jn)2
|
|
l-1
е
k=0
|
|
у
х |
xk+1
xk
|
Lnq(f(t)) t Jn(jnt) dt, n = 1,2,... | |
(5) | |
и
обозначено A0rl = Lnrf(1), A1rl = (Lnrf(1))ў, A0rk = Lnrf(xk - 0) - Lnrf(xk + 0), A1rk = (Lnrf(xk - 0))ў-Lnrf(xk + 0))ў, k = 1,..., l - 1, r = 1,...,q; ( (·)ў = d/dx(·) ).
3. Приведем свод
известных формул (см. главу 18 в [1] и формулы (55) и (58)-(61)из глав 7.2 и
7.15 в [2]), лежащих в основе дальнейшего исследования:
|
±nJn(x) + x Jn ў (x) = ±x
Jn-±1(x); | |
(6) | |
|
|
|
| Fn(x,X,z) = |
Ґ
е
n
= 1
|
|
Jn(x jn) Jn(X jn)
( jn2 - z2 ) J1 + n(jn)2
|
= | |
|
|
|
| = |
p Jn(x z) ( ( Jn(X z) Yn(z) ) -
Jn(z) Yn(X z) )
4 Jn(z)
|
, z П {±jn}, | |
(7) | |
где 0 Ј x Ј X Ј
1. Отсюда при z ® 0 (см.[2], глава 7)
|
|
|
| Fn(x,X,0) = |
Ґ
е
n
= 1
|
|
Jn(x jn) Jn(X jn)
jn2 J1 + n(jn)2
|
= |
p xn ( -1
+ X2 n )
csc(p n)
4 Xn G(1 - n) G(1 +
n)
|
. | |
(8) | |
Заметим, что если
перейти к пределу n ® 0 и
выражение справа примет вид logX /2.
Функция Fn(x,X,z) будет определена при любом z О C, если при целом положительном m и z = ±jm принять
|
|
|
| Fn(x,X,jm) = |
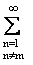
|
Jn(x jn) Jn(X jn)
( jn2 - jm2 ) J1
+ n(jn)2
|
= | |
|
|
|
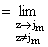 |
ж
з
и
|
Fn(x,X,z) -
|
Jn(x jm) Jn(X jm)
( j m2 - z2 ) J1 + n(jm)2
|
ц
ч
ш
|
, 0 Ј x Ј X Ј 1. | |
(9) | |
Предел в (9) справа существует и без труда
может быть представлен в явном виде (например, применением системы Mathematica, см. [10]).
Как известно (см., например, [1], главы 12 и
15), jn = p(n + n/2 - 1/4) + O(n-1) , n ® Ґ, и при x > 0 функция
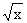 Jm(x) ограничена при
любом m і -1/2, а также |
Jm(x) ограничена при
любом m і -1/2, а также |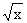 Jn+1(jn) | і
Jn+1(jn) | і const > 0. Отсюда следует равномерная сходимость рядов в
формулах (6)-(9) по указанным значениям x, X и z О C.
Рассмотрим теперь функцию (x О [0,1])
Учитывая асимптотику функций Бесселя на
бесконечности, функцию Gn можно
дифференцировать по x (при x № x), а также многократно
дифференцировать по w = z2.
4. Предположим
теперь, что нам известна функция fq(x) =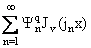 . Тогда разложение
fN(x) = fq(x) + . Тогда разложение
fN(x) = fq(x) +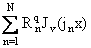 сходится к f(x) в
метрикеL2[(0,1),x] (см.[1]) со скоростью ||f - fN|| = o(N-2q+1), N ® Ґ. Тот же порядок равномерной
сходимости будет обеспечен и на отрезках вида [e,1], 0 < e < 1. сходится к f(x) в
метрикеL2[(0,1),x] (см.[1]) со скоростью ||f - fN|| = o(N-2q+1), N ® Ґ. Тот же порядок равномерной
сходимости будет обеспечен и на отрезках вида [e,1], 0 < e < 1.
Если нам известны только коэффициенты
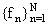 и точки {xk}, то
практическая реализация этой схемы ускоренной сходимости состоит из следующих
алгоритмов.
и точки {xk}, то
практическая реализация этой схемы ускоренной сходимости состоит из следующих
алгоритмов.
A. Нахождение
скaчков  , s = 0,1, k = 1,..., l - 1, r = 1,...,q. Для достаточно большого N и некоторого 0 <
d = , s = 0,1, k = 1,..., l - 1, r = 1,...,q. Для достаточно большого N и некоторого 0 <
d = |
const < 1 подберем целые значения
{ns} так, чтобы было dN Ј n1 < n2 < ј < np-1 <
np = N, p = 2(l + q), и найдем приближенные значения
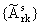 ,-с точностью ,-с точностью
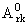 - -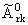 = o(N2(r-q)-1), = o(N2(r-q)-1),
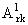 - -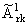 = o(N2(r-q)), N ® Ґ,-как решения линейной системы уравнeний = o(N2(r-q)), N ® Ґ,-как решения линейной системы уравнeний
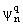 = 0, n = nr,
r = 1, 2 ,..., 2(l + q). Не останавливаясь на вопросах разрешимости этой системы,
отметим только, что, как показывают асимптотические формулы для функций Бесселя,
она аналогична соответствующей системе в КЭГ-методе.
= 0, n = nr,
r = 1, 2 ,..., 2(l + q). Не останавливаясь на вопросах разрешимости этой системы,
отметим только, что, как показывают асимптотические формулы для функций Бесселя,
она аналогична соответствующей системе в КЭГ-методе.
B. Нахождение функции
fq(x). Из формул и заключительных замечаний п.3 следует, что
суммы вида
|
Ґ
е
n=1
|
|
Jn(jn x) Jn(jn x)
Jn+1(jn)2
jn 2r
|
, |
Ґ
е
n=1
|
|
jn Jn(jn x) Jn ў(jn x)
Jn+1(jn)2
jn 2r
|
, r і 1 | |
(11) | |
явно выражаются
через функцию Gn(x,x,z) и ее соответствующие производные при z = 0. Таким
образом, функция fq(x) находится приближенно, в явном виде, с
использованием результатов алгоритма А.
Описанный алгоритм ускорения сходимости
(назовем его алгоритмом AB или АВ-методом) является естественным
распространением КЭГ-метода наразложения Фурье-Бесселя, причем в роли полиномов
Бернулли выступают упомянутые значения функции Gn(x,x,z) и ее производных при
z = 0.
5. Переходя к
распространению результатов работы [8] на ряды Фурье-Бесселя, заметим, что в
представлении (5) для коэффициентов {Ynq},-при каждом фиксированном индексе
суммирования k,-фигурируют два асимптотических ряда, соответственно по четным и
нечетным степеням jn-1. При q
і 2 к каждому из них применим аппроксимацию Паде для
рядов по степеням w = jn-2
некоторого, зависящего от k, порядка [M/m], M + m = (q - 1), m і 1 (см.[9]).
В результате этой основной процедуры,
вместо упомянутых коэффициентов {Ynq}, будут фигурировать следующие:
| Fnq = |
l
е
k=1
|
xk |
ж
з
и
|
jn 2(mk1-Mk1) |
Jn(jnxk) Pk1(jn2)
Jn+1(jn) Qk1(jn2)
|
+ jn 2(mk2-Mk2) |
jn Jn ў(jnxk) Pk2(jn2)
Jn+1(jn)2 Qk2(jn2)
|
ц
ч
ш
|
, n і
1, | |
(12) | |
где
Pks и Qks-многочлены от
jn2 порядков (Mks-1) и
mks соответственно, s = 1,2.
Здесь мы приходим к алгоритму, основанному на
явном виде функции jq(x) =
 . .
C. Нахождение
функции jq(x). Разложив
рациональные функции Pks(x)/Qks(x),
s = 1,2, на простые дроби, нетрудно убедиться, что функция jq(x) является линейной комбинацией значений
Gn(x,x,z), ее
первых производных по x, x
№ x, и (r - 1) производных по
w = z2, при x = xk, но уже при
z2 = wkts, k = 1, ..., l; t = 1, ...mks, s = 1,2, где
величины {wkts} зависят от нулей знаменателей примененных
аппроксимаций Паде, а r-максимум их кратности. Таким образом, функция jq(x) также находится приближенно (с учетом
результатов алгоритма А), в явном виде.
На этот раз,-уже по известной функции jq(x),-найдем разложение gN(x) = jq(x) +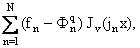 которое,-при условии
нахождения скачков с достаточной точностью,-сходится (см. [9]) к f(x) (как и
fN) со скоростью ||f - gN|| = o(N-2q+1), N ® Ґ. которое,-при условии
нахождения скачков с достаточной точностью,-сходится (см. [9]) к f(x) (как и
fN) со скоростью ||f - gN|| = o(N-2q+1), N ® Ґ.
Алгоритм A+C (назовем его алгоритмом AC или
АС-методом) является естественным аналогом алгоритма квазиполиномиального
разложения работы [8].
6. Численную
реализацию алгоритмов АВ и АС проиллюстрируем в простейшем (и наиболее важном
для приложений) случае, когда f(x)-гладкая при x О
(0,1] функция, удовлетворяющая в окрестности нуля указанным выше условиям. В
этом случае, пользуясь известными формулами для функцийБесселя, из (5)
(учитывая, что Jn(jn) = 0 и l = 1), получим
| Ynq = |
2 jn
Jn+1(jn)
|
|
q
е
r=0
|
Ar jn-2 r, Ar = Ar10, A0 = 0 n
і 1. | |
(13) | |
Продифференцировав формулу (7) по X, получим
при X®1 (Gўn = dGn /dX,см.
также (6))
|
|
|
| Gўn(1,x,z) = |
Ґ
е
n
= 1
|
|
jn Jn(x jn)
( jn2 - z2 ) J1 + n(jn)
|
= |
Jn(x z)
2Jn(z)
|
. | |
(14) | |
Дифференцируя теперь Gўn(1,x,z) по
z2 и устремляя z®0, найдем суммы рядов
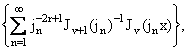 r = 0,1, ..., в виде явных
функций, являющихся в АВ-методе аналогами полиномов Бернулли в КЭГ-методе. Вот
как выглядят первые три из них (r = 0,1,2): r = 0,1, ..., в виде явных
функций, являющихся в АВ-методе аналогами полиномов Бернулли в КЭГ-методе. Вот
как выглядят первые три из них (r = 0,1,2):
|
м
н
о |
xn, |
xn
(1 - x2 )
4 ( 1 + n)
|
, |
xn ( x2 -1) ( -3 - n+
x2 ( 1 + n) )
32 ( 1 + n) 2 ( 2 +
n)
|
ь
э
ю |
. | |
Заметим теперь, что, как нетрудно видеть, что
для g(x) О Cq[0,1], q і 1 и n і
-1/2 функция f(x) = xng(x2) удовлетворяет всем условиям,
приведенным в п.2 выше.
Алгоритмы АВ и АС применялись к такой функции
|
f(x) = xn ( cos(25 x) + log(1 +
x2) ). | |
(15) | |
Эксперимент проводился на персональном
компьютере применениемсистемы Mathematica
([10]). Предполагалось, что q = 2 p-четное и в алгоритме С к разложению
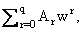 w = jn-2, применялась диагональная аппроксимация Паде порядка
[p/p]. w = jn-2, применялась диагональная аппроксимация Паде порядка
[p/p].
Таблица 1
L2([0,1],x) - относительные ошибки применения
алгоритмов АВ
и АС к функции (15) при N = 50
|
|
|
|
q = 0 |
q = 2 |
q = 4 |
q = 6 |
q = 8 |
|
|
| n = -1/4 |
AB
|
1.3e-1 |
1e-5 |
5.6e-9 |
8.5e-5 |
3.7e-0 |
|
AC |
1.3e-1 |
7e-6 |
5.7e-12 |
4.2e-13 |
3.4e-13 |
|
|
| n = 0 |
AB
|
1.5e-1 |
1.3e-5 |
6e-9 |
6.5e-6 |
1.8e-1 |
|
AC |
1.5e-1 |
7.8 e-6 |
8.8e-12 |
7e-13 |
6.5e-13 |
|
|
| n = e » 2.7 |
AB
|
2.6e-1 |
1.9e-5 |
5.1e-9 |
2.8e-9 |
9.2e-6 |
|
AC |
2.6e-1 |
1.1e-5 |
6e-10 |
4.2e-13 |
3.5e-13 |
|
Коэффициенты {fn}, n = 1,2,...,50, вычислялись применением автоматического интегрирования, с погрешностью порядка
10-11. Спектр {ln}, n = 1, 2, ..., 50, вычислялся применением
дополнительного пакета системы Mathematica.
Некоторые результаты экспериментов приведены
в табл. 1, в которойданные при q = 0 соответствуют ошибкам усеченного ряда
Фурье-Бесселя (1), состоящего из первых 50 членов.
В алгоритме А было выбрано значение d = .3 и,-с целью достижения большей точности,-скачки
 k = 1, 2, ..., q, определялись при q = 10, а затем их значения
использовались для q Ј 8. k = 1, 2, ..., q, определялись при q = 10, а затем их значения
использовались для q Ј 8.
Как это следует из табл. 1, ряд (1)
сходится очень медленно и даже сумма его первых 50 членов дает погрешность,
превосходящую 10%. В то же время алгоритмы АВ и АС,-использующие те же 50 первых
коэффициентов ряда (1),-приводят к резкому увеличению точности. При этом
алгоритм АВ достаточно эффективен для q Ј 4, однако уже
при q = 6 он становится чувствительным как к ошибкам в определении скачков, так
и к ошибкам округления, а при q = 8 и n Ј 1 становится практически неприменимым. В то же время
алгоритм АС не только всегда дает лучшие результаты (а при q і 4-более точные на несколько порядков), но и гораздо
устойчивей. Кроме того, он позволяет выявлять спектральные характеристики
функции f(x). Так, при n = 0 и p = 8 в явном виде функции
jq(x) содержится слагаемое
10.288 J0(24.9935 x), что указывает на наличие частоты
24.9935/p, при реально содержащейся в функции f(x)
частоте 25/p. Заметим, что абсолютные значения
коэффициентов {fn} имеют два пика: один при n = 7 и другой (вдвое
больший) при n = 9. Учитывая, что j 6 »
18 и j10 » 30.6, приходим к выводу, что
прежде, на основе анализа любого количества коэффициентов {fn}, можно
было локализовать эту частоту только где-то на интервале (18.5/p,30/p).
Табл. 2 дает представление о величинах
скачков {|A k|}, k = 1, 2, ...,10, и погрешностях при их приближенном
определении. Первая ее строка содержит номера индексов скачков, вторая-порядки
абсолютных значений их величин, а третья-соответствующие относительные
погрешности | Ak -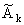 | / |Ak|. | / |Ak|.
Как видим, вместе с ростом величин скачков
соответственно быстро возрастает и относительная ошибка определения скачков.
Скачки [A\tilde]9 и [A\tilde]10 нами не использовались.
Таблица 2
Порядки абсолютных значений величины первых 10 скачков
{Ak}, k = 1, 2, ...,10,
функции (15) (n =
0) и относительная погрешность при их приближенном
вычислении на этапе А при
N = 50
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
| 2e+0 |
6e+2 |
4e+5 |
2e+8 |
2e+11 |
e+14 |
e+17 |
e+19 |
e+22 |
e+25 |
|
|
| 8e-12 |
4e-9 |
3e-7 |
1e-5 |
3e-4 |
4e-3 |
5e-2 |
3e-1 |
1e+0 |
2e+0 |
|
Тем не менее, несмотря на такие
чувствительные погрешности в определении скачков, применение алгоритмов АB и
(особенно) AC вполне оправдывается.
Таблица 3
L2([0,1],x) - относительные ошибки применения
алгоритмов АВ
и АС к функции (15) при n = 0, N = 50
и точном вычислении скачков
|
|
|
|
q = 0 |
q 0 =2 |
q = 4 |
q = 6 |
q = 8 |
|
|
| n = 0 |
AB
|
1.5e-1 |
1.3e-5 |
6e-9 |
4.4e-6 |
1.3e-1 |
|
AC |
1.5e-1 |
7.8 e-6 |
1e-11 |
1.4e-14 |
7e-15 |
|
В этой связи интересно сравнить результаты
табл. 1 для n = 0 с соответствующими вычислениями,
проведенными с использованием практически точных скачков, полученных применением
символьного дифференцирования системы Matematica. Из
табл. 3, в частности, следует, что алгоритм АB (в отличие от алгоритма АC)
весьма чувствителен к ошибкам округления.
Работа выполнена в рамках проекта ISTC A-823.
Институт математики НАН РА
Литература
1. Ватсон Г.Н. Теория Бесселевых функций. Ч. 1. М. ИЛ.
1949.
2. Бейтмен Г., Эрдейи
А. Высшие трансцендентные
функции. Т. 2. М. Наука. 1974.
3.
Jerri A. J. - Contemporary Mathematics. 1995.
V. 190. P.179-194.
4. Scherberg
M.G. Doctor of Philosophy's Thesis. Univ. of Minnesota.
1931. 11 p.
5. Крылов
А. Лекции по приближенным
вычислениям. Л. Изд. АН
СССР. 1933.
6. Gottlieb D.,
Shu C.W. - Math. Comp. 1992. V. 43. P. 81-92.
7. Eckhoff K.S. - Math. Comp. 1995. V. 64. N 210. P.
671-690.
8. Нерсесян
А.Б. - ДНАН Армении. 2004. Т. 104. N 4. С.
186-191.
9. Бейкер Дж.,
Грейвс-Моррис П. Аппроксимации Паде. М. Мир. 1986.
502 с.
10. Wolfram
S. The MATHEMATICA book. Fourth Edition. Wolfram
Media. Cambridge University Press. 1999. 1468 p.
|
![]() Lnqf(x)) О
L2(0,x1) . Отсюда и из (4), учитывая поведение
Jn(x) при x ® 0
(см.[1,2]), придем к асимптотическому разложению вида fn = Ynq + Rn q по
степеням jn-1 с точностью до
Rnq = o(n-2q), n ® Ґ, где
Lnqf(x)) О
L2(0,x1) . Отсюда и из (4), учитывая поведение
Jn(x) при x ® 0
(см.[1,2]), придем к асимптотическому разложению вида fn = Ynq + Rn q по
степеням jn-1 с точностью до
Rnq = o(n-2q), n ® Ґ, где ![]()
![]()
![]() Jm(x) ограничена при
любом m і -1/2, а также |
Jm(x) ограничена при
любом m і -1/2, а также |![]() Jn+1(jn) | і
Jn+1(jn) | і ![]() . Тогда разложение
fN(x) = fq(x) +
. Тогда разложение
fN(x) = fq(x) +![]() сходится к f(x) в
метрикеL2[(0,1),x] (см.[1]) со скоростью ||f - fN|| = o(N-2q+1), N ® Ґ.
сходится к f(x) в
метрикеL2[(0,1),x] (см.[1]) со скоростью ||f - fN|| = o(N-2q+1), N ® Ґ. ![]() и точки {xk}, то
практическая реализация этой схемы ускоренной сходимости состоит из следующих
алгоритмов.
и точки {xk}, то
практическая реализация этой схемы ускоренной сходимости состоит из следующих
алгоритмов.![]() , s = 0,1, k = 1,..., l - 1, r = 1,...,q. Для достаточно большого N и некоторого 0 <
d =
, s = 0,1, k = 1,..., l - 1, r = 1,...,q. Для достаточно большого N и некоторого 0 <
d =![]() ,-с точностью
,-с точностью
![]() -
-![]() = o(N2(r-q)-1),
= o(N2(r-q)-1),
![]() -
-![]() = o(N2(r-q)), N ® Ґ,-как решения линейной системы уравнeний
= o(N2(r-q)), N ® Ґ,-как решения линейной системы уравнeний
![]() = 0, n = nr,
r = 1, 2 ,..., 2(l + q). Не останавливаясь на вопросах разрешимости этой системы,
отметим только, что, как показывают асимптотические формулы для функций Бесселя,
она аналогична соответствующей системе в КЭГ-методе.
= 0, n = nr,
r = 1, 2 ,..., 2(l + q). Не останавливаясь на вопросах разрешимости этой системы,
отметим только, что, как показывают асимптотические формулы для функций Бесселя,
она аналогична соответствующей системе в КЭГ-методе.![]() .
.![]() которое,-при условии
нахождения скачков с достаточной точностью,-сходится (см. [9]) к f(x) (как и
fN) со скоростью ||f - gN|| = o(N-2q+1), N ® Ґ.
которое,-при условии
нахождения скачков с достаточной точностью,-сходится (см. [9]) к f(x) (как и
fN) со скоростью ||f - gN|| = o(N-2q+1), N ® Ґ.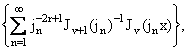 r = 0,1, ..., в виде явных
функций, являющихся в АВ-методе аналогами полиномов Бернулли в КЭГ-методе. Вот
как выглядят первые три из них (r = 0,1,2):
r = 0,1, ..., в виде явных
функций, являющихся в АВ-методе аналогами полиномов Бернулли в КЭГ-методе. Вот
как выглядят первые три из них (r = 0,1,2): ![]() w = jn-2, применялась диагональная аппроксимация Паде порядка
[p/p].
w = jn-2, применялась диагональная аппроксимация Паде порядка
[p/p].
![]() k = 1, 2, ..., q, определялись при q = 10, а затем их значения
использовались для q Ј 8.
k = 1, 2, ..., q, определялись при q = 10, а затем их значения
использовались для q Ј 8.![]() | / |Ak|.
| / |Ak|.