МАТЕМАТИКА

УДК 517.538.5

В. А. Мартиросян, А. З. Мартиросян

Многократно T-универсальные функции, представимые лакунарными
степенными рядами

(Представлено академиком Н.У. Арзуманяном 15/I 2004)

   В настоящей работе продолжено исследование вопросов конструирования голоморфных функций, представимых степенными рядами с наперед заданными лакунами и многократно универсальных (в том или ином смысле) относительно определенной простой последовательности операций, сохраняющей лакуны исходного степенного ряда начатое в [1]. Полученные в указанной статье результаты относились к случаю целых функций. В данной работе аналогичные вопросы рассматриваются для функций, голоморфных в круге или голоморфных в произвольном открытом множестве, имеющем только односвязные компоненты связности.
   Отметим, что похожие вопросы конструирования многократно универсальных голоморфных функций без контроля лакун их степенных рядов исследовались в ряде статей В. Луха (см. [2,3]). Отметим также, что подробную информацию о развитии теории универсальных функций и полную библиографию вплоть до 1999 г. можно найти в обзоре К. Гроссе-Эрдмана [4]. Более позднии исследования, естественно, связанные с нашей работой, представлены, например, в [5-11].
   Чтобы сформулировать основные результаты статьи, введем некоторые обозначения и понятия. Для компактного множества K из конечной комплексной плоскости C обозначим через A(K) Банахово пространство из всех непрерывных на K и голоморфных на его внутренности комплекснозначных функций с нормой ||f|| = sup{|f(z)| : z О K}. Обозначим через M семейство всех компактов K М C со связным дополнением C \ K. Для множества E М C будем обозначать E ее границу. Как обычно, пусть N, Z будут множества, соответственно, из всех натуральных и целых чисел; пусть также N0 = N И {0}. Для подпоследователсьности Q = {qn}nОN0 из N0 положим n(t) - количество ее членов из отрезка [0,t] и определим верхнюю и минимальную плотности для Q следующим образом:

   Пусть функция f голоморфна в односвязной области G М C. Последовательность операций { Lj}jОZ определим следующим образом: для z О G и j О N0 положим L0f(z) = f(z), L1f(z) = (zf(z))ў, Ljf(z) = L1(Lj-1f(z)) при j = 2, 3, ј; для z О G и j = -1, -2, ј  положим

Ljf(z) = м
п
п
н
п
п
о
z-1 z
у
х
0 
 Lj+1f(t)dt,
если   0 О G
z-1 z
у
х
z0 
 Lj+1f(t)dt,
если   0 П G,  z0 О G,

где интеграл берется по любой спрямляемой дуге из G, соединяющей, соответственно, 0 или z0 с z.
   Пусть даны произвольные открытое множество O М C, 0 О O, и подпоследовательность Q из N0. Обозначим через HQ(O) множество всех голоморфных на O функций j, представимых в некоторой окрестности нуля лакунарным степенным рядом
j(z) = Ґ
е
n=0 
 jnzn,    jn = 0   при   n П Q.

В частности, при O = C для кратности полагаем HQ(C) = EQ.
   Определение. Пусть O М C - произвольное открытое множество. Функция j называется T-универсальной на O ("универсальной относительно трансляций"), если она голоморфна на O и имеет следующее свойство: для всех K О M, для всех f О A(K) и для всех V О O существуют последовательности {an}nОN и {bn}nОN такие, что anz + bn О O для всех z О K и всех n О N, последовательность {anz + bn}nОN сходится к V и последовательность {j(anz + bn)}nОN сходится к f(z) равномерно на K.
   Основными  результатами  статьи  являются  приведенные  ниже  теоремы 1-3. Первая из них относится к случаю целых функций. Далее рассматриваются   функции,   голоморфные,   соответственно,   на   круге   Dr = {z : |z| < r} с 0 < r < Ґ и на произвольном открытом множестве, имеющем только односвязные компоненты связности.
   Теорема 1. Пусть {zn}nОN0 - неограниченная последовательность комплексных чисел и Q - подпоследовательность из N0 с минимальной плотностью Dmin(Q) > 0. Тогда существует функция j такая, что при любом фиксированном j О Z функция Ljj(z) О EQ и последовательность {Ljj(z + zn)}nОN0 плотна в A(K) для всех K О M.
   Теорема 2. Пусть Q - подпоследовательность из N0 с минимальной плотностью Dmin(Q) > 0. Тогда существует функция j такая, что при любом фиксированном j О Z функция Ljj(z) О HQ(Dr) и T-универсальна.
   Теорема 3. Пусть O М C - открытое множество с односвязными компонентами, 0 О O, и пусть Q - подпоследовательность из N0 с верхней плотностью 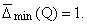Тогда существует функция j такая, что при любом фиксированном j О Z функция Ljj(z) О HQ(O) и T-универсальна.
   В заключение отметим, что доказательства теорем 1-3 основаны на новейших результатах теории комплексных приближений о возможности равномерного приближения многочленами с пропусками.

   Институт математики НАН РА
   Ереванский государственный университет

Литература

     1. Мартиросян В.А., Мартиросян А.З.  - Изв. НАН Армении. Математика. 2004. Т. 39. С. 5-11.
     2. Luh W.  - J.Approx. Theory. 1988. V. 53. P. 128-144.
     3. Luh W.  - J.Approx. Theory. 1997. V. 89. P. 135-155.
     4. Gross-Erdmann K.G.  - Bull. Amer. Math. Soc. 1999. V. 36. P. 345-381.
     5. Luh W., Martirosian V.A., Müller J.  - Indagationes Mathem. (N.S.). 1998. V. 9. P. 529-536.
     6. Luh W., Martirosian V.A., Müller J.  - Acta Sci. Math. (Szeged). 1998. V. 64. P. 67-79.
     7. Luh W., Martirosian V.A., Müller J.  - J.Approx. Theory. 2002. V. 114. P. 201-213.
     8. Gharibyan T., Luh W., Müller J.  - Analusis. 2003. V. 23. P. 199-214.
     9. Gharibyan T., Luh W.  - Annales Univ. Sci. Budapest. Sect. Comp. 2003. V. 22. P. 113-126.
     10. Gharibyan T., Luh W.  - Изв. НАН Армении. Математика. 2003. Т. 38. N 4. С. 51-64.
     11. Schillings B.  - Изв. НАН Армении. Математика. 2003. Т. 38. С. 85-94.