МАТЕМАТИКА
УДК 517
С. Л. Гогян
Подсистема Хаара как квазигриди базис
(Представлено чл.-кор. НАН РА Г.Г. Геворкяном 25/VI 2004)
Пусть Y =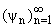 нормированный базис в Банаховом пространстве X. Для
любого элемента x О X будем иметь разложение
нормированный базис в Банаховом пространстве X. Для
любого элемента x О X будем иметь разложение
Обозначим spec(x) = {i О N; ci(x,Y) № 0}. Для элемента x О X,
перестановку натуральных чисел r, r(j) = kj, j = 1, 2, ј назовем
понижающим и будем писать r О
D(x), если
| |ck1(x,Y)| і |ck2(x,Y)| і ј. | |
В случае строгих неравенств, D(x) будет
содержать только одну перестановку. Определим m-ый гриди аппроксимант элемента x
по системе Y и перестановке r
О D(x) по формуле
| Gm(x) = Gm(x, Y, r) = |
m
е
j=1
|
ckj(x,Y)ykj. | |
Положим Lm(x,Y) = |ckm(x,Y)|. Заметим, что Lm(x,Y) определяется
однозначно и не зависит от понижающей перестановки r
О D(x).
Определение. Базис
Y называется квазигриди базисом, если для каждого
элемента x О X и для каждой перестановки r О D(x) имеет место
|
lim
m®Ґ
|
||x - Gm(x, Y, r)||X = 0. | |
Гриди базисы разных типов описаны В. Н.
Темляковым в работе [1].
Теорема [2]. Для
того, чтобы базис Y являлся квазигриди базисом,
необходимо и достаточно, чтобы для каждого элемента x О
X и перестановки r О D(x)
имело место
| ||Gm(x, Y, r)||X Ј C||x||X | |
(1) |
для некоторой постоянной C, не
зависящей от x и от m.
Из этой теоремы ясно, что если (1) имеет
место для одной перестановки r О D(x), то будет справедливым и для всех перестановок r О D(x).
Напомним определение ортогональной системы
Хаара
Здесь система Хаара нормирована по
L1 норме. Хорошо известно, что система Хаара является безусловным
базисом в Lp(0,1) при p > 1 и базисом в L1(0,1) (см.
например [3]). В работе [4] показано, что система Хаара не является квазигриди
базисом в L1(0,1). Там же построена возрастающая последовательность
натуральных чисел
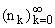 так, что подсистема Хаара
так, что подсистема Хаара
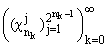 в L1(0,1) является квазигриди базисом на
своей линейной оболочке. Хотя конкретный вид последовательности
в L1(0,1) является квазигриди базисом на
своей линейной оболочке. Хотя конкретный вид последовательности
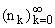 в [4] не
фигурирует, но можно показать, что она растет не медленнее, чем геометрическая
прогрессия. В частности для достаточно больших k имеет место
[(nk+1)/(nk)] > 2.
в [4] не
фигурирует, но можно показать, что она растет не медленнее, чем геометрическая
прогрессия. В частности для достаточно больших k имеет место
[(nk+1)/(nk)] > 2.
В данной работе под выражением ||f||D будем
подразумевать L1 норму функции f на интервале D. Напомним,
что система Хаара обладает свойством монотонности, т. е. для любых чисел
ak О R и m О N и
для любой возрастающей последовательности nk имеет место
| || |
m
е
k=1
|
akcnk||L1(0,1) Ј || |
m+1
е
k=1
|
akcnk||L1(0,1). | |
С применением этого свойства легко
доказывается
Лемма 1. Для любой
f О L1(0,1) и каждого n О N справедливо
Для любого n = 0, 1, 2, ј определим
| Q(2n) = |
м
н
о |
f : f = q0 + |
n
е
i=1
|
|
22i-1
е
j=1
|
qijcj2i, где |q0| Ј 1 и |qij| Ј 1; i = 1, 2, ј, n; j = 1, 2, ј, 22i-1 |
ь
э
ю |
| |
и
| Q(2n+1) = |
м
н
о |
f : f = |
n
е
i=0
|
|
22i
е
j=1
|
qijcj2i+1, где |qij| Ј 1; i = 0, 1, ј, n; j = 1, 2, ј, 22i |
ь
э
ю |
| |
Обозначим
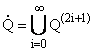 и
и
 Определим также
Определим также
| P(2n) = |
м
п
н
п
о
|
| f : f = p0 + |
n
е
i=1
|
|
22i-1
е
j=1
|
pijc2ij,
| |
| где
p0 = 0 или
|p0| і 1 и |pij| і 1
| |
|
|
| или
pij = 0; i = 1, 2, ј, n; j = 1, 2, ј, 22i-1 | | |
ь
п
э
п
ю
|
| |
и
| P(2n+1) = |
м
н
о |
f : f = |
n
е
i=0
|
|
22i
е
j=1
|
pijc2i+1j, где |pij| і 1 или |pij| = 0; i = 0, 1, ј, n;
j = 1, 2, ј, 22i |
ь
э
ю |
. | |
Если D является носителем функции из
системы Хаара с нижним индексом k, то скажем, что D является интервалом
Хаара размерности k.
Лемма 2. Пусть
D интервал Хаара размерности k і 1
Тогда для
любой функции f О Q(k-1) справедливо
Через
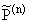 обозначим
множество всех функций p О P(n), которые
удовлетворяют условию: на любом интервале Хаара (a,b) размерности n - 2i - 1 і 1
(i = 0, 1, ј) справедливо
обозначим
множество всех функций p О P(n), которые
удовлетворяют условию: на любом интервале Хаара (a,b) размерности n - 2i - 1 і 1
(i = 0, 1, ј) справедливо
| "x О |
ж
з
и |
a, |
a + b
2
|
ц
ч
ш |
Ю p(x) = p |
ж
з
и |
x + |
b - a
2
|
ц
ч
ш |
. | |
Аналогично через
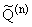 обозначим множество всех функций q О Q(n),
которые удовлетворяют условию: на любом интервале Хаара (a,b) размерности n - 2i - 1 і 1
(i = 0, 1, ј) справедливо
обозначим множество всех функций q О Q(n),
которые удовлетворяют условию: на любом интервале Хаара (a,b) размерности n - 2i - 1 і 1
(i = 0, 1, ј) справедливо
| "x О |
ж
з
и |
a, |
a + b
2
|
ц
ч
ш |
Ю q(x) = q |
ж
з
и |
x + |
b - a
2
|
ц
ч
ш |
. | |
Лемма 3. Пусть для
некоторого C > 0 и натурального n і 2 существуют
функции f О P(n) (f П P(n-2)) и q О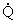 ,
если n нечетное (q О
,
если n нечетное (q О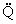 если n четное), так, что
если n четное), так, что
и
Тогда
существуют число 0 Ј i Ј n
и функции p, q так, что
1. n є i( mod 2),
2. p О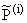 , ,
3. p П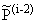 , q О , q О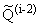 если i і 2
и q = 0 если
i = 0,1, если i і 2
и q = 0 если
i = 0,1,
4. ||p|| >
C| p+q||,
5. spec(p) З spec(q) = Ж.
Теорема 1. Пусть
функции p и q таковы, что для некоторой n і 2
1. p О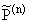 , p П , p П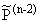
2. q О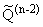 , ,
3. spec(p) З spec(q) = Ж.
Тогда
Из этой теоремы и леммы 3 выводится
Теорема 2. Пусть
для некоторого неотрицательного n функция p О
P(n) и p П P(n-2) (если n і 2).
Тогда для
любой функции q О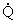 , если n нечетное
(q О , если n нечетное
(q О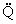 , если n четное), для которой spec(p) З spec(q) = Ж, справедливо , если n четное), для которой spec(p) З spec(q) = Ж, справедливо
Теорема
3. Подсистема
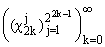 системы Хаара в L1(0,1) является
квазигриди базисом на своей линейной оболочке. системы Хаара в L1(0,1) является
квазигриди базисом на своей линейной оболочке.
Доказательство. Возьмем "f О span
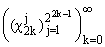 и m О N. и m О N.
1) Если Lm(f,c) = 0, то f - Gm(f) = 0 и следовательно ||Gm(f)|| = ||f|| Ј
3||f||.
2) Если Lm(f,c) № 0, то функция p(f) = [(Gm(f))/(Lm(f,c))] О P(2k) при некотором натуральном k, а функция
q(f) = [(f - Gm(f))/(Lm(f,c))] О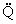 . Согласно теореме 2 . Согласно теореме 2
|
||Gm(f)||
Lm(f,c)
|
= ||p(f)|| Ј 3||p(f) + q(f)|| = |
||f||
Lm(f,c)
|
, | | а
это означает, что
Теорема доказана.
Точно так же доказывается
Теорема
4. Подсистема
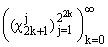 системы Хаара в L1(0,1) является
квазигриди базисом на своей линейной оболочке. системы Хаара в L1(0,1) является
квазигриди базисом на своей линейной оболочке.
Ереванский государственный
университет
Литература
1. Temlyakov V. N. - Found. Comput. Math. 2003. V. 3. P.
33-107.
2. Wojtashchyk P.
- J. of Approximation Theory. 2000. V. 107. P.
293-314.
3. Кашин Б. С., Саакян
А. А. - Ортогональные ряды. М. АФЦ.
1999.
4. Dilworth S. J.,
Kutzarova D., Wojtashchyk P. - J. of Approximation Theory.
2002. V. 114(2). P. 214-241.
|
![]() так, что подсистема Хаара
так, что подсистема Хаара
![]() в L1(0,1) является квазигриди базисом на
своей линейной оболочке. Хотя конкретный вид последовательности
в L1(0,1) является квазигриди базисом на
своей линейной оболочке. Хотя конкретный вид последовательности
![]() в [4] не
фигурирует, но можно показать, что она растет не медленнее, чем геометрическая
прогрессия. В частности для достаточно больших k имеет место
[(nk+1)/(nk)] > 2.
в [4] не
фигурирует, но можно показать, что она растет не медленнее, чем геометрическая
прогрессия. В частности для достаточно больших k имеет место
[(nk+1)/(nk)] > 2.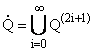 и
и
 Определим также
Определим также ![]() обозначим
множество всех функций p О P(n), которые
удовлетворяют условию: на любом интервале Хаара (a,b) размерности n - 2i - 1 і 1
(i = 0, 1, ј) справедливо
обозначим
множество всех функций p О P(n), которые
удовлетворяют условию: на любом интервале Хаара (a,b) размерности n - 2i - 1 і 1
(i = 0, 1, ј) справедливо ![]() обозначим множество всех функций q О Q(n),
которые удовлетворяют условию: на любом интервале Хаара (a,b) размерности n - 2i - 1 і 1
(i = 0, 1, ј) справедливо
обозначим множество всех функций q О Q(n),
которые удовлетворяют условию: на любом интервале Хаара (a,b) размерности n - 2i - 1 і 1
(i = 0, 1, ј) справедливо ![]() ,
если n нечетное (q О
,
если n нечетное (q О![]() если n четное), так, что
если n четное), так, что ![]() ,
,![]() , q О
, q О![]() если i і 2
и q = 0 если
i = 0,1,
если i і 2
и q = 0 если
i = 0,1,![]() , p П
, p П![]()
![]() ,
,![]() , если n нечетное
(q О
, если n нечетное
(q О![]() , если n четное), для которой spec(p) З spec(q) = Ж, справедливо
, если n четное), для которой spec(p) З spec(q) = Ж, справедливо ![]() системы Хаара в L1(0,1) является
квазигриди базисом на своей линейной оболочке.
системы Хаара в L1(0,1) является
квазигриди базисом на своей линейной оболочке.![]() и m О N.
и m О N.![]() . Согласно теореме 2
. Согласно теореме 2 ![]()