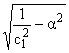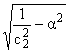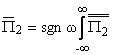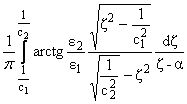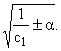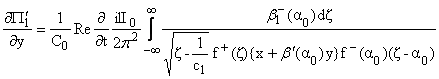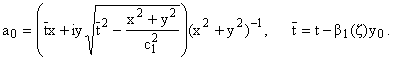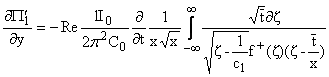ФИЗИКА
УДК 539.1
Член-корреспондент НАН РА А. Г. Багдоев, А. Н.
Мартиросян,
Г. А. Мартиросян
Распространение электромагнитных волн в двухслойной среде
от
вибратора при наличии идеально проводящего полубесконечного
экрана
(Представлено 27/I 2004)
Рассматривается линейная электродинамическая
задача о расчете действия импульсного вибратора, находящегося в верхней
полуплоскости (x,y), при наличии на отрицательной части оси x идеально
проводящего экрана.
Соотношения
электродинамики между компонентами электрического и магнитного полей и
компонентой П вектора Герца имеют вид [1]
| Hx = 0,
Hy = 0, Ez = 0,
Hz = |
¶2 P
¶x¶t
|
, | |
| Ex = |
c
e
|
|
¶2P
¶x¶y
|
, Ey = - |
1
c
|
|
¶2P
¶t2
|
+ |
c
e
|
|
¶2P
¶y
|
, | |
(1) |
где c - скорость света в пустоте,
e - диэлектрическая проницаемость. Урaвнения Максвелла
для верхней и нижней полуплоскостей имеют вид:
|
¶2P1
¶x2
|
+ |
¶2P1
¶y2
|
- |
1
c12
|
|
¶2P1
¶t2
|
= -lI0d(x)d(y - y0)d(t), | |
|
¶2P2
¶x2
|
+ |
¶2P2
¶y2
|
= |
1
c22
|
|
¶2P2
¶t2
|
, | |
(2) |
где c1,2 - скорость света
в полуплоскостях.
Граничные условия на линии
контакта полуплоскостей имеют вид: y = 0,
| P1 = P2, |
1
e1
|
|
¶P1
¶y
|
= |
1
e2
|
|
¶P2
¶y
|
, 0 < x < Ґ; | |
|
¶P1
¶y
|
= 0, |
¶P2
¶y
|
= 0, -Ґ < x <
0; | |
| P1,P2 = 0(r11/2),
r1 |
|
_____
Цx2 + y2
|
®
0. | |
(3) |
В
верхней полуплоскости можно записать
| P1 = P10 + P1ў, P10 = |
м
п
п
н
п
п
о
|
|
| |
(4) |
где [c/(4p)]I0 - сила тока в вибраторе, l - длина диполя,
P10 есть решение задачи об
импульсе в бесконечной плоскости, r2 = x2 + (y - y0)2.
Решение находится методом интегральных преобразований и сводитcя к
системе Винера - Хопфа, которая решается обычным способом [2]. Вводя
преобразования по Лапласу
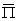 от P по t, можно
полагать
от P по t, можно
полагать
|
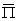 10 = 10 =
|
ilI0
2p
|
sgn w |
Ґ
у
х
-Ґ
|
|
eiw{ax-b1(a)(y-y0)}
2b1(a)
|
da, | |
b1(a) =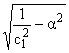 , b2(a) = - , b2(a) = -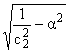 |
|
(5) |
|
 (a)eiw(ax+b1y)da, (a)eiw(ax+b1y)da, | |
|
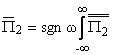 (a)eiw(ax+b2y)da, (a)eiw(ax+b2y)da, | |
где
s = -iw есть параметр
преобразования Лапласа, две черточки соответствуют преобразованиям Лапласа по t
и Фурье по x. Из граничних условий (3) и (5) следуют соотнoшения
|
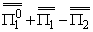 = E+(a), = E+(a),
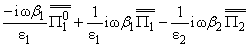 = F+(a), = F+(a), |
|
-iwb1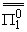 + iwb1 + iwb1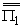 = G-(a), = G-(a), | |
iwb2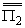 = H-(a), = H-(a),
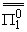 = ilI0(4pb1)-1eib1(a)wyo. = ilI0(4pb1)-1eib1(a)wyo. | |
Здесь индексы ± соответствуют функциям,
аналитическим в верхней и нижней полуплоскости a.
Исключая
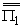 и и
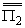 из (6), получим
систему Винера - Хопфа из (6), получим
систему Винера - Хопфа
|
1
e1
|
G-(a) - |
1
e2
|
H-(a) = F+(a). | |
(7) |
Из
второго уравнения (7), так как F+(a)
аналитично в верхней полуплоскости, выражение [1/(e1)]G-(a)-[1/(e2)]H-(a) - в нижней полуплоскости и F+(a) согласно граничному условию (3) в бесконечности равно
нулю, по теореме Лиувилля имеем F+(a) є 0, [1/(e1)]G-(a)-[1/(e2)]H-(a) є 0. Тогда H-(a) = [(e2)/(e1)]G-(a). Подставляя полученное выражение для H-(a) в первое уравнение (7),
получим
|
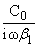 f(a)G-(a) = E+(a) - 2 f(a)G-(a) = E+(a) - 2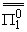 , , |
|
(8) |
| f(a) = |
1
C0
|
|
ж
з
и |
1- |
b1
b2
|
|
e2
e1
|
|
ц
ч
ш |
, C0 = 1 + |
e2
e1
|
. | | Так
как f(a) ® 1 при a ® Ґ, то
согласно теореме C [2] можно написать
где f+(a) и f-(a) aналитично соответственно в верхней и нижней
полуплоскостях плоскости a
| ln f-(a) = - |
1
2pr
|
|
Ґ
у
х
-Ґ
|
ln f(z) |
dz
z - a
|
. | |
(10) |
Здесь путь интегрирования совпадает с вещественной осью и обходит точки
ветвления z = -[1/(c1)], -[1/(c2)] сверху, точки ветвления z = [1/(c1)], [1/(c2)] снизу и точку
z = a сверху. В формуле (9)
путь интегрирования деформируем так, что он проходит по обоим берегам рaзреза
вдоль вещественной оси от [1/(c1)] до +Ґ.
После выбора ветвей функций b1, b2 легко вычислить ln f-(a) в виде
ln f-(a) =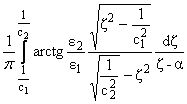 є j-(a), є j-(a), |
|
(11) |
| f±(a) = exp(j±(a)), f+(a) = f-(-a). | | Из уравнений (8), (9), (11) получим
|
C0
iw
|
|
f-(a)
b1-(a)
|
G-(a) = |
b1+(a)
f+(a)
|
E+(a) - |
2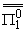 b1+(a) b1+(a)
f+(a)
|
, | |
(12) |
b1(a) = b1+(a)b1-(a),
b1±(a) =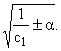
|
| Обозначим g(a) = -[(ilI0)/(2pb1-(a)f+(a))]eiwb1(a)y0.
Так как g(a) ~ [const /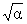 ] при a ® Ґ, то можно функцию g(a) представить в виде [2] ] при a ® Ґ, то можно функцию g(a) представить в виде [2]
где g-(a) = -[(ilI0)/(4p2)]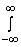 [(eiwb1(z)y0dz) / [(eiwb1(z)y0dz) /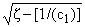 f+(z)(z - a)], g+(a) = g(a) - g-(a). f+(z)(z - a)], g+(a) = g(a) - g-(a).
Из формулы (12), (13) получим
|
C0
iw
|
|
f-(a)
b1-(a)
|
G-(a) - g-(a) = |
b1+(a)E+(a)
f+(a)
|
+ g+(a)
є I(a). | |
(14) |
Фyнкция I(a) определена лишь на вещественной
оси. Однако функция I(a) в формуле (14), написанной c
индексом (-), определена и аналитична в нижней полуплоскости, а функция с
индексом (+) аналитична в верхней полуплоскости a.
Таким образом аналитическим продолжением функцию I(a)
можно определить на всей плоскости a.
Из граничных условий (3) видно, что I(a) ® 0 при a ® Ґ. Тогда
по теореме Лиувилля функция I(a) є 0, т.е.
|
C0
iw
|
|
f-(a)
b1-(a)
|
G-(a) - g-(a) = 0, | |
|
b1+(a)E+(a)
f+(a)
|
+ g+(a) = 0. | |
(15) | Переходя к обратным преобразованиям Лапласа и Фурье, получим [3]
|
¶Pў1
¶y
|
= |
1
2pi
|
|
s+iw
у
х
s-iҐ
|
ds |
Ґ
у
х
-Ґ
|
es(t-ax-b1y)G-(a)da. | |
(16) |
Вычисляя интегралы в формуле (16) по s и затем по a, можно получить решения в форме Смирнова - Соболева
|
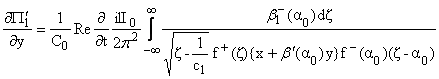
|
(17) |
Определим поведения решений при y = 0, x ~ 0,
a ® Ґ,
g-(a) ~ [1/(a)],
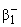 (a) ~ i (a) ~ i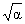 , d = [t/x] , d = [t/x]
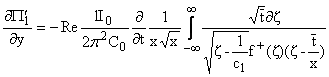 . . | |
(18) | или
Институт меxаники НАН
РА
Гориcский филиал ГИУА
Литература
1. Кошляков Н. С., Глинер Э.
Б., Смирнов М. М. Уравнения в частных производных математической
физики. М. Высшая школа. 1970. 710 с.
2. Нобл В. Применение метода Винера - Хопфа для решения
дифференциальных уравнений с частными производными. М. ИЛ. 1962. 279
с.
3. Багдоев А. Г. - Изв. АН АрмССР. Механика. 1974. Т. 27. N 2. С. 13-23.
| ![]() и
и
![]() из (6), получим
систему Винера - Хопфа
из (6), получим
систему Винера - Хопфа