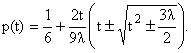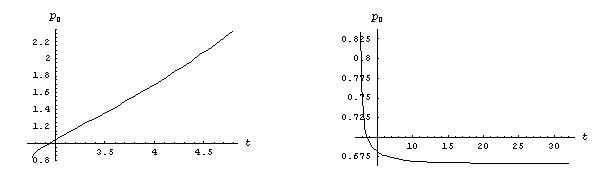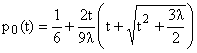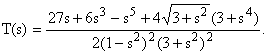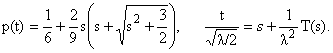ФИЗИКА
УДК 539.016
А. М. Ишханян
Вероятность перехода в нелинейной задаче Ландау - Зинера в
пределе сильной связи
(Представлено академиком Р. А. Казаряном 12/I 2004)
Динамика перехода Ландау - Зинера [1] в
модели двухмодовой фотоассоциации [2] атомарного бозе-эйнштейновского конденсата
[3] по схеме одноцветного облучения лазерным полем в приближении вращающейся
волны может быть описана с помощью следующего нелинейного обыкновенного
дифференциального уравнения третьего порядка для вероятности молекулярного
состояния p(t) [4,5]:
| pўўў - |
pўў
t
|
+ 4[t2 + l(1 - 3p)]pў + |
l
2t
|
(1 - 8p + 12p2) = 0, | |
(1) |
где l =
U02/d0 - параметр
Ландау - Зинера, U0 - частота Раби лазернoго поля, d0 - параметр, определяющий скорость прохождения
нуля расстройки частоты (предполагается, что интенсивность возбуждающего
лазерного поля поддерживается постоянной, а расстройка проходит через резонанс,
изменяясь во времени линейно: U0 = const, dt = d0t).
Ранее нами было показано [6], что в пределе
сильного взаимодействия l >> 1, когда эволюция
системы проявляет значительные отклонения от линейного режима, пригодное нулевое
приближение к решению задачи можно построить, отбросив в уравнении (1) два
первых члена с производными второго и третьего порядков. Получающееся нелинейное
уравнение первого порядка имеет богатую структуру, и его решения позволяют
конструировать равномерное приближение, которое затем может быть использовано
для построения всюду удовлетворительного следующего приближения путем
линеаризации уравнения (1). В силу того, что общее решение предельного уравнения
первого порядка известно, представленная схема описания предела сильной связи
может служить в качестве общего подхода для изучения всех аналогичных моделей
пересечения термов.
Описанным выше путем
удается выявить наиболее существенные черты происходящих процессов и с
достаточно хорошей точностью описать неадиабатические переходы в конденсате
количественно. Эффективность данного подхода была продемонстрирована нами на
примере первой экспоненциальной модели пересечения термов Никитина в работе [6],
где было показано, что предел сильного взаимодействия, как это ни странно, не
оптимален для образования молекул. Было обнаружено, что оптимум для перехода в
молекулярное состояние достигается при определенном конечном значении
интенсивности лазерного поля. В настоящей работе с использованием этого подхода
мы изучаем предел сильного взаимодействия для модели Ландау - Зинера
(противоположный предел слабого взаимодействия для данной модели был представлен
нами в предыдущих работах [4,5]). Мы строим подходящие нулевое и первое
приближения к решению задачи и выводим простую асимптотическую формулу для
вероятности перехода в молекулярное состояние для больших значений параметра
Ландау - Зинера.
Итак, учитывая порядки
членов, входящих в уравнение (1), сохраним сначала два последних слагаемых:
| 4[t2 + l(1 - 3p)]pў + |
l
2t
|
(1 - 8p + 12p2) = 0. | |
(2) |
Как
было отмечено в работе [6], это уравнение, несмотря на простой вид, обладает
богатой структурой. У него два тривиальных решения: p = 1/6 и p = 1/2. Эти решения
играют важную роль в установлении асимптот при t ® Ґ, поскольку представляют собой стационарные решения
уравнения (1). Например, в случае вышеупомянутой первой экспоненциальной модели
пересечения термов Никитина асимптотический предел вероятности образования
молекул в пределе сильных интенсивностей поля есть 1/6 [6]. Как мы убедимся
ниже, в настоящем случае модели Ландау - Зинера аналогичный предел суть 1/2,
т.е. второе тривиальное решение.
Общее
решение уравнения (2), зависящее от произвольной постоянной C, довольно сложное
[6]. Выбором различных значений данной постоянной получаются различные
независимые решения. В частности, существуют следующие четыре подобных решения:
|
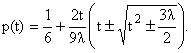
|
(3) |
Здесь допустимы все комбинации со знаками + и -. Эти решения показаны на pис.1,2. Заметим, что два из
решений, а именно те, что со знаком минус под корнем, не определены на всей
вещественной оси (pис.2). Поскольку ни одно из двух оставшихся решений не
ограничено на бесконечном временном интервале, то ясно, что ни одно из решений
(3) само по себе не может задавать пригодное приближенное решение начального
уравнения (1). (Условие нормировки еще больше ограничивает область применимости
(3)).
Асимптотический анализ показывает, что
в режиме сильной связи, при l =
U02/d0 ® Ґ, предельное решение задачи Ландау
- Зинера с наложенным здесь начальным условием p(-Ґ) = 0 можно компоновать из кусков различных решений (см.
pис.3, верхняя ломаная кривая), а именно, нетривиального
|
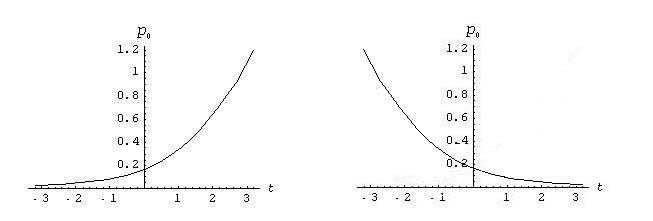
Рис. 1. Различные нетривиальные решения уравнения (2).
|
|
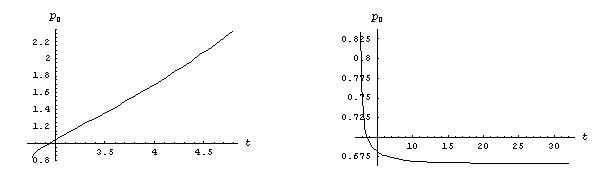
Рис. 2. Различные нетривиальные решения уравнения (2).
|
|
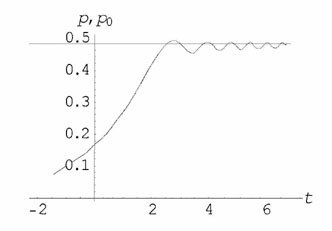
Рис. 3. Вероятность перехода в молекулярное состояние как функция от времени
в пределе
сильного взаимодействия верхняя ломаная кривая - предельное
решение (4)-(5),
горизонтальная линия - конечная вероятность перехода (14).
|
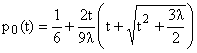 при t < при t <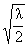 |
|
(4) |
и тривиального
|
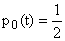 при t > при t >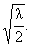
|
. | |
(5) |
Это
составное решение является довольно хорошим приближением повсюду, кроме малой
окрестности точки t =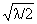 , где вдобавок производные испытывают разрыв. Далее, важно заметить, что
полученное предельное решение позволяет линеаризировать начальное уравнение (1)
с помощью подстановки p = p0 + u. В результате, пренебрегая (малыми)
нелинейными слагаемыми, получаем следующее линейное уравнение:
, где вдобавок производные испытывают разрыв. Далее, важно заметить, что
полученное предельное решение позволяет линеаризировать начальное уравнение (1)
с помощью подстановки p = p0 + u. В результате, пренебрегая (малыми)
нелинейными слагаемыми, получаем следующее линейное уравнение:
| uttt - |
1
t
|
utt + 4[t2 + l(1 - 3p0)]ut - |
4l
t
|
(1 - 3p0 + 3p0tt)u + |
ж
з
и |
p0ttt - |
1
t
|
p0tt |
ц
ч
ш |
= 0. | |
(6) |
В
области t >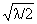 , когда
p0(t) = 1/2, это уравнение заметно упрощается:
, когда
p0(t) = 1/2, это уравнение заметно упрощается:
| uttt - |
1
t
|
utt + 4[t2 - l/2]ut - |
2l
t
|
u = 0. | |
(7) |
Полученное уравнение решается точно. Решение можно выразить через
произведения вырожденных гипергеометрических функций [7]:
| ut > l/2 = C1u1 + C2u2 + C3u3, | |
(8) |
| u1 = |
1
2
|
- 1F1(il/8; 1/2; id0t2)1F1(-il/8; 1/2; -id0t2), | |
(9) |
| u2 = tRe[1F1(il/8; 1/2; id0t2)1F1(1/2 - il/8; 3/2; -id0t2)], | |
(10) |
| u3 = tIm[1F1(il/8; 1/2; id0t2)1F1(1/2 - il/8; 3/2; -id0t2)]. | |
(11) |
Однако в области t <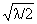 , где p0(t) задается выражением (4), точное
решение линеаризированного уравнения (6) неизвестно. Тем не менее, рассмотрение
порядков членов в уравнении (6) показывает, что высшие производные u малы.
Следовательно, мы можем построить следующее по порядку асимптотическое
приближение, пренебрегая членом (uttt - utt/t). Это приводит к несколькo громоздкой
формуле, которая, однако, дает превосходное приближение для области t Ј 0:
, где p0(t) задается выражением (4), точное
решение линеаризированного уравнения (6) неизвестно. Тем не менее, рассмотрение
порядков членов в уравнении (6) показывает, что высшие производные u малы.
Следовательно, мы можем построить следующее по порядку асимптотическое
приближение, пренебрегая членом (uttt - utt/t). Это приводит к несколькo громоздкой
формуле, которая, однако, дает превосходное приближение для области t Ј 0:
| ut Ј
0 = - |
1
l2
|
|
1
3(1 - t2)2
|
|
й
к
л |
|
t(17 + 5t2 + 2t4)
2(3 + t2)3/2
|
+ |
(6 + 13t2 + 4t4 + t6)
(3 + t2)2
|
|
щ
ъ
ы |
, t =
|
t
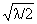 |
. | |
(12) |
Заметим, что в точке пересечения термов t = 0 вероятность перехода близка
к 1/6: p0(0) + ut Ј 0(0) = 1/6 - 2/(9l2), в то время как
в аналогичном линейном случае она примерно есть 1/2. Это - общее наблюдение,
присущее всем нелинейным моделям с пересечением
термов.
Недостаток решения (12) состоит в
том, что оно расходится при t =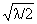 . Ясно, что это расхождение является следствием наличия
сингулярности в уравнении (1) в точке t = 0. Чтобы получить равномерно сходящееся
разложение, применим метод растянутых параметров [7]. Вводя новую переменную,
задаваемую выражением
. Ясно, что это расхождение является следствием наличия
сингулярности в уравнении (1) в точке t = 0. Чтобы получить равномерно сходящееся
разложение, применим метод растянутых параметров [7]. Вводя новую переменную,
задаваемую выражением
| t = s + |
1
l2
|
T(s) + O |
ж
з
и |
|
1
l3
|
|
ц
ч
ш |
, | |
(13) |
легко получаем, что расхождение
будет устранено, если положить
|
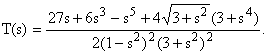
|
(14) |
Следовательно, корректное приближение первого порядка записывается в
параметрическом виде:
|
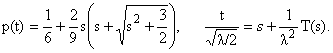 |
(15) |
(Интересно, что это разложение справедливо также и в области t >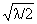 , поскольку оно
определяет монотонно возрастающую функцию, стремящуюся к 1/2 при t ® Ґ. Точность приближения есть
величина по крайней мере порядка 1/l.)
, поскольку оно
определяет монотонно возрастающую функцию, стремящуюся к 1/2 при t ® Ґ. Точность приближения есть
величина по крайней мере порядка 1/l.)
Более точное выражение
для приближения первого порядка в области 0 < t <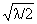 можно получить, применяя
метод растянутых параметров Линдштедта - Пуанкаре [8]. Это дает:
можно получить, применяя
метод растянутых параметров Линдштедта - Пуанкаре [8]. Это дает:
| ×(2t2 - 2 |
Ц
|
6l
|
t + 3(3 + l))(6+l)(3+2l)/(4l(3+l)). | |
(16) |
Формулы (12), (16) и (8), взятые вместе, дают хорошее приближение для
всей области t О (-Ґ, +Ґ) и для всех l >> 1 (относительная ошибка везде порядка 10-3). Сшивка решений (16) и (8) в точке t =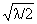 +
+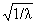 ведет к следующему
принципиальному результату: конечная вероятность перехода в молекулярное
состояние в режиме сильного взаимодействия приблизительно выражается с помощью
линейной формулы Ландау - Зинера PLZ(l) = 1 - e-pl с
параметром l, замененным на l/2:
ведет к следующему
принципиальному результату: конечная вероятность перехода в молекулярное
состояние в режиме сильного взаимодействия приблизительно выражается с помощью
линейной формулы Ландау - Зинера PLZ(l) = 1 - e-pl с
параметром l, замененным на l/2:
| p(+Ґ) » |
PLZ(l/2)
2
|
|
ж
з
и |
1 - |
4
3pl
|
PLZ(l/2) |
ц
ч
ш |
. | |
(17) |
Сравнение рассчитанной с помощью формул (8)-(12) и (16) вероятности
перехода как функции от времени с численным решением точного уравнения (1) в
рассмотренном пределе сильного взаимодействия показано на pис.3, где показаны
также предельное решение (4)-(5) и конечная вероятность перехода (17). Как
видно, согласие очень хорошeе.
Работа
выполнена при поддержке грантов Фонда Гражданских Исследований и Разработок США
(CRDF) No. PH 100-02 и РА No. 0591-2002.
Инженерный центр НАН РА
Литература
1. Landau L. D. - Phys. Z. Sowjetunion. 1932. N 2. P. 46; Zener C. -
Proc. R. Soc. London. A. 1932. V. 137. P. 696.
2. Javanainen J., Mackie M. - Phys. Rev. A.
1999. V. 59. P. R3186; Koštrun M., Mackie M., Cote R., Javanainen
J. -Phys. Rev. A 2000.V. 62. P. 063616.
3. Anderson M. H., Ensher J. R., Matthews M. R., Wieman C.
E., Cornell E. A. - Science. 1995. V. 269. P. 198; Anglin J.R.,
Ketterle W. - Nature (London). 2002. V. 416. P. 211.
4. Ишханян А. М., Черников Г. П. - Изв. НАН
Армении. Физика. 2004. Т. 39. N1, С. 3-10.
5. Ишханян А. М. - ДНАН Армении. 2004. Т.
104. N 2. С. 112-118.
6. Ишханян А. М. - Изв. НАН Армении. Физика. 2004. Т. 39. N2.
С. 71-77.
7. Abramowitz M.,
Stegun I. A. Handbook of Mathematical Functions. New York, Dover.
1965.
8. Nayfeh A. H. Perturbation Methods. New York, Wiley-Interscience. 1985.
![]() , где вдобавок производные испытывают разрыв. Далее, важно заметить, что
полученное предельное решение позволяет линеаризировать начальное уравнение (1)
с помощью подстановки p = p0 + u. В результате, пренебрегая (малыми)
нелинейными слагаемыми, получаем следующее линейное уравнение:
, где вдобавок производные испытывают разрыв. Далее, важно заметить, что
полученное предельное решение позволяет линеаризировать начальное уравнение (1)
с помощью подстановки p = p0 + u. В результате, пренебрегая (малыми)
нелинейными слагаемыми, получаем следующее линейное уравнение: ![]() , где p0(t) задается выражением (4), точное
решение линеаризированного уравнения (6) неизвестно. Тем не менее, рассмотрение
порядков членов в уравнении (6) показывает, что высшие производные u малы.
Следовательно, мы можем построить следующее по порядку асимптотическое
приближение, пренебрегая членом (uttt - utt/t). Это приводит к несколькo громоздкой
формуле, которая, однако, дает превосходное приближение для области t Ј 0:
, где p0(t) задается выражением (4), точное
решение линеаризированного уравнения (6) неизвестно. Тем не менее, рассмотрение
порядков членов в уравнении (6) показывает, что высшие производные u малы.
Следовательно, мы можем построить следующее по порядку асимптотическое
приближение, пренебрегая членом (uttt - utt/t). Это приводит к несколькo громоздкой
формуле, которая, однако, дает превосходное приближение для области t Ј 0: ![]() . Ясно, что это расхождение является следствием наличия
сингулярности в уравнении (1) в точке t = 0. Чтобы получить равномерно сходящееся
разложение, применим метод растянутых параметров [7]. Вводя новую переменную,
задаваемую выражением
. Ясно, что это расхождение является следствием наличия
сингулярности в уравнении (1) в точке t = 0. Чтобы получить равномерно сходящееся
разложение, применим метод растянутых параметров [7]. Вводя новую переменную,
задаваемую выражением ![]() , поскольку оно
определяет монотонно возрастающую функцию, стремящуюся к 1/2 при t ® Ґ. Точность приближения есть
величина по крайней мере порядка 1/l.)
, поскольку оно
определяет монотонно возрастающую функцию, стремящуюся к 1/2 при t ® Ґ. Точность приближения есть
величина по крайней мере порядка 1/l.)![]() можно получить, применяя
метод растянутых параметров Линдштедта - Пуанкаре [8]. Это дает:
можно получить, применяя
метод растянутых параметров Линдштедта - Пуанкаре [8]. Это дает:
![]() +
+![]() ведет к следующему
принципиальному результату: конечная вероятность перехода в молекулярное
состояние в режиме сильного взаимодействия приблизительно выражается с помощью
линейной формулы Ландау - Зинера PLZ(l) = 1 - e-pl с
параметром l, замененным на l/2:
ведет к следующему
принципиальному результату: конечная вероятность перехода в молекулярное
состояние в режиме сильного взаимодействия приблизительно выражается с помощью
линейной формулы Ландау - Зинера PLZ(l) = 1 - e-pl с
параметром l, замененным на l/2: