УДК 539.3
А. А. Атоян, С. О. Саркисян
Изучение свободных колебаний микрополярных упругих тонких
пластин
(Представлено академиком С. А. Амбарцумяном 3/IX 2004)
В последние годы моментная теория упругости
привлекала внимание многих исследователей. Стало весьма актуальным исследование
задач о влиянии моментных напряжений на деформированное и напряженное состояние
тонких пластин и оболочек [1]. В монографии [1] на основе общих положений
общеизвестной уточняющей теории пластин и оболочек [2] и несимметричной теории
упругости создана прикладная-двумерная теория микрополярных пластин и оболочек.
В [3] построена общая статическая асимптотическая теория микрополярных упругих
тонких пластин, в [4] - общая динамическая прикладная-двумерная теория
микрополярных упругих тонких пластин.
Целью
настоящей работы является выяснение особенностей и степени влияния моментных
напряжений и микрополярности материала пластинки на характеристики динамических
процессов (в данном случае на характеристики свободных колебаний), происходящих
в тонких пластинках различных очертаний.
1. Рассмотрим свободные колебания шарнирно-опертой микрополярной балки. Задачу
будем изучать исходя из общей прикладной-одномерной динамической теории тонких
балок [4-6], как в случае, когда в ее основе имеем плоскую задачу динамической
несимметричной теории упругости (НТУ) с независимыми полями перемещений и
вращений (НППВ), так и в случае, когда в ее основе лежит плоская динамическая
задача НТУ с стесненным вращением (СВ).
Разрешающая система уравнений поперечных
(изгибных) колебаний (в условиях отсутствия внешних воздействий, как моментных,
так и силовых) микрополярных балок в перемещениях и вращениях выражается так
[4-6]:
|
м
п
п
н
п
п
о
|
|
4ma
m + a
|
|
ж
з
и
|
|
¶2W
¶x12
|
+ |
¶O2
¶x1
|
|
ц
ч
ш
|
= r |
¶2W
¶t2
|
, | |
|
|
| B* |
¶2O2
¶x12
|
- |
4ma
m + a
|
|
ж
з
и
|
|
¶W
¶x1
|
+ O2 |
ц
ч
ш
|
= J |
¶2O2
¶t2
|
, | | |
| |
(1.1) |
где W - прогиб, O2 -
поворот вокруг оси x3 (оси x1 и x2 расположены
в плоскости полосы-прямоугольника); r и J - плотность и
мера инерции при вращении материала микрополярной балки, между которыми
существует связь [7,8]
| J = |
4(l + m)
3l + 2m
|
rl2,
где l2 = |
g + e
2m
|
, | |
(1.2) |
характерная длина l зависит от
формы и размеров микроэлемента; l, m, a, B* = g + e - упругие константы материала
балки. К этим уравнениям следует присоединить граничные условия шарнирного
опирания, которые в данном случае запишутся следующим образом [4-6]:
| при x1 = 0,a W = 0, L12 = 0. | |
(1.3) |
Решение системы (1.1) ищем в форме
| W = Asin |
npx1
a
|
coswnt, O2 = Bcos |
npx1
a
|
coswnt, | |
(1.4) |
которая удовлетворяет условиям
шарнирного опирания по торцам стержня (A,B - неопределенные постоянные, n -
целое число).
Подставляя значения W,
O2 из (1.4) в (1.1), получим систему алгебраических однородных
уравнений относительно неизвестных A,B. Для существования нетривиальных решений
системы (1.1) необходимо, чтобы определитель ее был равен нулю. Приравнивая нулю
определитель полученной однородной алгебраической системы, для определения
частот собственных колебаний микрополярных балок получим следующее биквадратное
уравнение:
| rJwn4 - |
й
к
л |
B* |
n2
a2
|
p2r + |
4ma
m + a
|
r + |
4ma
m + a
|
|
n2
a2
|
p2J |
щ
ъ
ы |
wn2 + |
4ma
m + a
|
B* |
n4
a4
|
p4 = 0 | |
(1.5) |
Здесь легко заметить, что рассматривая задачу по микрополярной теории
пластин со свободным вращением, имеем определенные динамические эффекты, по
сравнению с классической теорией. Один из таких эффектов - появление двух групп
частот вместо одной, появляющейся в соответствующей задаче по классической
теории упругости.
Рассмотрим задачу об
определении частот и собственных форм изгибных колебаний шарнирно-опертых балок
на основе теории, когда вращения точек стеснены. Уравнение поперечных свободных
колебаний и граничные условия микрополярной балки в этом случае будут выражатся
следующим образом [5]:
| D* |
¶4W
¶x14
|
= 2h |
¶2
¶t2
|
|
ж
з
и |
J |
¶2W
¶x12
|
- rW |
ц
ч
ш |
, | |
(1.6) |
| при x1 = 0,a, W = 0, M11 + L12 = 0, | |
(1.7) |
где
D* = 2hB* + [(2Eh3) / (3(1 - v2))].
Решение
уравнения (1.6) при граничных условиях (1.7) ищем в форме
В
итоге для определения частот свободных колебаний микрополярных стержней на
основе НТУ с СВ получим
На
основе уравнений (1.5) для определения частот микрополярных балок по НТУ с НППВ
и формулы (1.9) для определения частот по НТУ с СВ были проведены некоторые
численные расчеты. Основываясь на результатах полученных численных данных,
проведен численный анализ и выявлены динамические эффекты микрополярности
материала балки. Для получения численных результатов нужно конкретизировать
материальные константы стержня как по классической теории упругости, так и по
микрополярной теории упругости, которые входят в уравнения для определения
частот колебаний. С этой точки зрения используем значения материальных констант,
полученных в результате динамических экспериментов в работах [7,8]. Эти значения
модулей упругости приведены для зернистого композита: алюминиевая дробь в
эпоксидной матрице (табл.1).
Таблица 1
| l |
m |
a |
B* = g + e |
J |
| Г Па
|
Г Па
|
М Па
|
к Н |
кг/м |
| 7.59 |
1.89 |
7.45 |
2.64 |
0.429 · 10-3
|
Целью проведения численого анализа является
сопоставление частот, полученных по прикладной-одномерной динамической теории
балок на основе плоской задачи НТУ с НППВ (частоты, определяемые уравнением
(1.5)), а также на основе плоской задачи НТУ с СВ (частоты, определяемые
уравнением (1.9)), с частотами классической теории упругости и, кроме того,
изучение диапазонов схождения и расхождения этих трех типов частот полученных по
трем разным прикладным теориям.
Частоты
собственных изгибных колебаний балки по классической теории упругости
определяются на основе следующей формулы [9]:
| wn2 = |
r
|
, где
D = |
2Eh3
3(1 - v2)
|
. | |
(1.10) |
Имея в виду (1.4), (1.8), (1.9) и (1.10), определим
соотношения
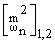 /
/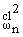 и
и
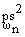 /
/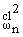 по формулам:
по формулам:
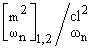
|
= |
3(3l + 2m)(l + 2m)
16(l + m)2
|
|
a4
p4h2l2n4
|
|
м
н
о |
|
й
к
л |
|
2a
m + a
|
+ |
n2
a2
|
l2p2 + |
2a
m + a
|
|
4(l + m)
3l + 2m
|
|
n2
a2
|
l2p2 |
щ
ъ
ы |
± | |
| ± |
ж
ъ
Ц
|
|
й
к
л
|
|
2a
m + a
|
+ |
n2
a2
|
l2p2 + |
2a
m + a
|
|
4(l + m)
3l + 2m
|
|
n2
a2
|
l2p2 |
щ
ъ
ы
|
2
|
- |
8a
m + a
|
|
4(l + m)
3l + 2m
|
|
n4
a4
|
l4p4 |
|
|
ь
э
ю |
, | |
|
ps2
wn
|
|
/ |
|
cl2
wn
|
= |
й
к
л |
|
l2
h2
|
|
3(l + 2m)
2(l + m)
|
+ 1 |
щ
ъ
ы |
|
/ |
|
й
к
л |
l2p2 |
4(l + m)
(3l + 2m)
|
|
n2
a2
|
+ 1 |
щ
ъ
ы |
, | |
(1.12) |
где
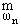 - частоты, полученные по моментной теории
упругости с НППВ;
- частоты, полученные по моментной теории
упругости с НППВ;
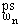 - частоты,
полученные по моментной теории упругости с СВ;
- частоты,
полученные по моментной теории упругости с СВ;
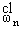 - частоты, полученные по классической теории
упругости. В (1.11) и (1.12) a - длина стержня. В табл. 2-5 приведены численные
данные, полученные на основе значений модулей упругости, приведенных в табл. 1,
и формул (1.11) и (1.12).
- частоты, полученные по классической теории
упругости. В (1.11) и (1.12) a - длина стержня. В табл. 2-5 приведены численные
данные, полученные на основе значений модулей упругости, приведенных в табл. 1,
и формул (1.11) и (1.12).
|


|
Исходя из приведенных численных данных можно
прийти к следующим выводам.
Если расчеты
вести на основе прикладной теории микрополярных балок с СВ, то частота колебаний
окажется выше частоты классической теории. Этот вывод соответствует другим
исследованиям в этой области [10]. Для более массивной микрополярной балки
частоты, вычисляемые по теории НТУ с СВ, уже приближаются к частотам по
классической теории. Если основываться на прикладной теории микрополярных балок
по НТУ с НППВ, в отличие от теории с СВ (где имеем одну группу частот), получим
две группы частот. В численных выражениях по теории со свободным вращением
получаем сразу высшую частоту и одну низкую частоту.
2. Рассмотрим теперь свободные изгибные колебания шарнирно-опертых
микрополярных упругих прямоугольных пластин. Задачу будем изучать как исходя из
общей прикладной-двумерной динамической теории тонких пластин, когда в ее основе
имеем НТУ с НППВ [4,5], так и исходя из общей прикладной динамической двумерной
теории тонких пластин, когда в ее основе лежит трехмерная НТУ с СВ
[5].
Разрешающая система уравнений поперечных
(изгибных) колебаний (в условиях отсутствия внешних воздействий как моментных,
так и силовых) микрополярных прямоугольных пластин в перемещениях и вращениях
имеет вид [4,5]:
|
м
п
п
п
п
п
п
п
п
п
н
п
п
п
п
п
п
п
п
п
о
|
|
4ma
m + a
|
|
ж
з
и
|
|
¶2W
¶x12
|
+ |
¶2W
¶x22
|
+ |
¶O2
¶x1
|
- |
¶O1
¶x2
|
|
ц
ч
ш
|
= r |
¶2W
¶t2
|
, | |
|
|
|
4g(g + b)
2g + b
|
|
ж
з
и
|
|
¶2O1
¶x12
|
+ |
¶2O2
¶x1¶x2
|
|
ц
ч
ш
|
+ (g + e) |
ж
з
и
|
|
¶2O1
¶x22
|
- |
¶2 O2
¶x1¶x2
|
|
ц
ч
ш
|
+ | |
|
|
| + |
4ma
m + a
|
|
ж
з
и
|
|
¶W
¶x2
|
-
O1 |
ц
ч
ш
|
= J |
¶2O1
¶t2
|
, | |
|
|
|
4g(g + b)
2g + b
|
|
ж
з
и
|
|
¶2O2
¶x22
|
+ |
¶2O1
¶x1¶x2
|
|
ц
ч
ш
|
+ (g + e) |
ж
з
и
|
|
¶2O2
¶x12
|
- |
¶2 O1
¶x1¶x2
|
|
ц
ч
ш
|
- | |
|
|
| - |
4ma
m+a
|
|
ж
з
и
|
|
¶W
¶x1
|
+ O2 |
ц
ч
ш
|
= J |
¶2O2
¶t2
|
. | | |
| |
(2.1) |
К
этим уравнениям следует присоединить граничные условия шарнирного опирания,
которые в данном случае запишутся следующим образом [5]:
| при x1 = 0,a
W = 0, O1 = 0,
L12 = 0, | |
| при x2 = 0,b
W = 0, O2 = 0, L21 = 0, | |
где
a и b размеры пластинки в плане.
Решение
системы (2.1) ищем в форме
| W = Asin |
mpx1
a
|
sin |
npx2
b
|
coswmnt, O1 = Bsin |
mpx1
a
|
cos |
npx2
b
|
coswmnt, | |
| O2 = Ccos |
mpx1
a
|
sin |
npx2
b
|
coswmnt, | |
которая
удовлетворяет всем условиям шарнирного опирания по всему контуру пластинки
(A,B,C - неопределенные постоянные, m и n - целые
числа).
Подставляя значения
W,O1,O2 из (2.3) в (2.1), получим систему алгебраических
однородных уравнений относительно неизвестных A,B,C. Для существования
нетривиальных решений системы (2.1) необходимо, чтобы определитель ее был равен
нулю.
Приравнивая нулю определитель
полученной однородной алгебраической системы, для определения частот собственных
колебаний микрополярных упругих прямоугольных пластин получим следующие
уравнения:
| Jw2mn = |
4g(g + b)
2g + b
|
|
ж
з
и |
|
m2
a2
|
+ |
n2
b2
|
|
ц
ч
ш |
p2 + |
4ma
m + a
|
, | |
(2.4) |
| rJw4mn - |
й
к
л |
(g + e) |
ж
з
и |
|
m2
a2
|
+ |
n2
b2
|
|
ц
ч
ш |
p2r + |
4ma
m + a
|
r + |
4ma
m + a
|
|
ж
з
и |
|
m2
a2
|
+ |
n2
b2
|
|
ц
ч
ш |
p2J |
щ
ъ
ы |
w2mn + | |
| + |
4ma
m + a
|
(g + e) |
ж
з
и |
|
m2
a2
|
+ |
n2
b2
|
|
ц
ч
ш |
2
|
p4 = 0. | |
Pассмотрим аналогичную задачу определения частот и собственных форм
изгибных колебаний шарнирно-опертых пластин на основе теории, когда вращения
точек стеснены [5]. Уравнение поперечных свободных колебаний и граничные условия
микрополярных прямоугольных пластин будут выражаться следующим образом [5]:
| D*С2С2W = 2h |
ж
з
и |
JС2 |
¶2W
¶t2
|
- r |
¶2W
¶t2
|
|
ц
ч
ш |
, | |
(2.6) |
| при x1 = 0,a W = 0, M11 + L12 = 0, | |
| при x2 = 0,b W = 0, M22 - L21 = 0, | |
где D* = 2h(g + e) + [(2Eh3)/(3(1 - v2))], С2 = [(¶2)/(¶x12)] + [(¶2)/(¶x22)].
Решение уравнения (2.6) при граничных
условиях (2.7) ищем в форме
| W = Asin |
mpx1
a
|
sin |
npx2
b
|
coswmnt. |
|
(2.8) |
В итоге для определения частот свободных колебаний микрополярных
прямоугольных пластин на основе НТУ с СВ получим
| w2mn= |
D*
2h
|
|
ж
з
и |
|
m2
a2
|
+ |
n2
b2
|
|
ц
ч
ш |
p4 |
/ |
|
ж
з
и |
Jp2 |
ж
з
и |
|
m2
a2
|
+ |
n2
b2
|
|
ц
ч
ш |
+ r |
ц
ч
ш |
. | |
(2.9) |
На
основе уравнений (2.4)-(2.5) для определения частот по НТУ с НППВ и, на основе
уравнения (2.9) для определения частот по НТУ с СВ, были проведены численные
расчеты.
Уравнение для определения частот по
классической теории упругости имеет вид [9]
|
cl2
wmn
|
= |
D
2h
|
|
ж
з
и |
|
m2
a2
|
+ |
n2
b2
|
|
ц
ч
ш |
2
|
p4 |
/ |
r, где D = |
2Eh3
3(1 - v2)
|
. | |
(2.10) |
Сравнивая уравнения определения частот колебаний пластинки (2.4), (2.5)
по НТУ с НППВ с уравнением (2.9) по НТУ с СВ и уравнением (2.10) по классической
теории, можем сделать заключение, что по теории со свободным вращением имеются
три группы частот, а по теории со стесненным вращением и по классической теории
имеется одна группа частот. Что касается численных данных, то здесь тоже
обнаруживаются те же закономерности для частот колебаний, что и для
микрополярных балок, кроме этого, в случае пластинки существуют частоты, которые
зависят от физической константы b (формула (2.4)).
Гюмрийский государственный педагогический
институт им. М. Налбандяна
Литература
1. Амбарцумян С. А. Микрополярная теория оболочек и пластин. Ереван. Изд-во НАН Армении.
1999. 214 с.
2. Амбарцумян С.
А. Теория анизотропных пластин. М. Наука.
1967. 266с.
3. Саркисян С. О. -
Сб. науч. трудов, посвященных 80-летию академика НАН РА С. А.
Амбарцумяна. Ереван. Изд-во НАН РА. 2002. С. 285-296.
4. Атоян А. А., Саркисян С. О.
- Экологический вестник научных центров Черноморского
экономического сотрудничества. 2004. №1. С. 18-29.
5. Atoyan A. A., Sargsyan S. H. - Book of
Abstracts. International Symposium on Trends in Applications of Mathematics to
Mechanics. August 22-28. 2004. Lufthansa Bildungszentrum Seeheim, Germany. P. 5.
6. Атоян А. А. - Матер. 12 республиканской конф. молодых ученых. Механика. Ереван. 2003.
С. 31-36.
7. Ерофеев В. И. Волновые процессы в твердых телах с микроструктурой. М. Изд-во
МГУ. 1999. 327 с.
8. Gauther R.
D. Jahsman W. E. - Arch. Mech. 1981. V. 33. N 5. P.
717-737.
9. Тимошенко С. П. Колебания в инж. деле. М. Физматгиз. 1959. 439
с.
10. Бабич Д. В. Некоторые динамические задачи теории пластин и оболочек с несимметричным
тензором напряжений. Ин-т механики АН УССР. Киев. 1967. 12 с.

