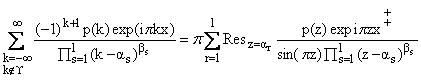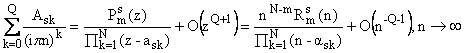ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
УДК 519.65
Академик А. Б. Нерсесян
Квазиполиномы типа Бернулли и ускорение сходимости рядов
Фурье
кусочно-гладких функций
(Представлено 24/IХ 2004)
1. Пусть f = f(x) -
кусочно-гладкая на отрезке [-1,1] функция, с точками
"склеивания" {ak}, -1 Ј a1 < ј <
a\l < 1, 1 Ј l < Ґ, и f О
CQ+1, Q > 1 на каждом из отрезков
[ak,ak+1] . Обозначим через
Ask = f(k)(as - 0) - f(k)(as + 0), (k = 0,1,ј,Q, s = 1, ј, l) скачки f и ее
производных в точках {as}. Удобно считать f 2-периодической (т.е.
заданной на окружности) и, таким образом, al+1 = a1 и если
a1 = -1, то a1 - 0 = 1 - 0, a1 + 0 = -1 + 0. Для коэффициентов Фурье
функции f,
| fn = |
1
2
|
|
у
х |
1
-1
|
f(t)e-ipn tdt, n = 0, ± 1, ± 2,ј | |
(1) |
нетрудно получить (интегрироваием по
частям) следующую формулу (n № 0):
| fn = |
(-1)n+1
2
|
|
l
е
s=1
|
exp(ipnas) |
Q
е
k=0
|
|
Ask
(ipn)k+1
|
+ |
1
2 (ipn)Q+1
|
|
l
е
s=1
|
|
у
х |
as+1
as
|
f(Q+1)(t)e-ipn
tdt. | |
(2) |
Рассмотрим многочлены Бернулли, определяемые рекурентной формулой
| B0(x) = |
x
2
|
, Bk(x) = |
у
х |
Bk-1(x)dx, x О [-1,1], k = 1,2, ј, | |
где
константа интегрирования вычисляется из условия
 Bk(t)dt = 0, k = 1,2,ј. На всю действительную ось многочлены {Bk(x)}
продолжаются периодически, с периодом 2, и являются кусочно-полиномиальными
функциями с коэффициентами Фурье Bk,n = (-1)n+1/ (2(ipn)k+1), n = 0, ± 1, ± 2, ј.
Bk(t)dt = 0, k = 1,2,ј. На всю действительную ось многочлены {Bk(x)}
продолжаются периодически, с периодом 2, и являются кусочно-полиномиальными
функциями с коэффициентами Фурье Bk,n = (-1)n+1/ (2(ipn)k+1), n = 0, ± 1, ± 2, ј.
Формула (2) позволяет
представить функцию f в виде f(x) = WQ(x) + w(x) где WQ(x) -
кусочно-полиномиальная функция, состоящая из линейной комбинации сдвигов
многочленов Бернулли, а w(x) - некоторая, Q раза непрерывно дифференцируемая на
действительной оси и 2-периодическая, функция. Коэффициенты Фурье
{wn} функции w(x) имеют порядок убывания, равный, по меньшей мере,
o(n-Q-1), n
® Ґ. Поэтому аппроксимационная
формула f(x) = WQ(x) +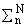 =-Nwneipn x сходится к f со скоростью порядка o(N-Q), N ® Ґ.
=-Nwneipn x сходится к f со скоростью порядка o(N-Q), N ® Ґ.
Проблема вычисления
скачков {Ask} посредством конечного количества коэффициентов Фурье
{fn}, |n|
Ј N, сводится к решению системы уравнений,
возникающей из (2) отбрасыванием интегральных членов. Важно отметить, что такой
подход применим и в случае , когда, вместо коэффициентов Фурье, известно
дискретное преобразование Фурье значений функции f на равномерной сети (cм.
[4]).
Вышеизложенный метод ускорения
сходимости отрезка ряда Фурье предварительным вычитанием из f
кусочно-полиномиальной функции восходит к работам А. Крылова (см. [1], 1933 г.).
В последнее десятилетие интерес к нему особенно усилился, и он был развит и
усовершенствован, в разных направлениях, главным образом, усилиями К. Эркгофа и
Д. Готтлиба (см., например, [2,4-6]). Поэтому такой подход будем называть
КЭГ-методом (см. также работы [3,7,8]).
2. Пусть {as
} ,s = 1, ..., l, 1 Ј l < Ґ - некоторое конечное множество комплексных чисел и
¡ Н {as } - его подмножество целых чисел
(возможно, пустое).
Лемма. Справедлива формула
|
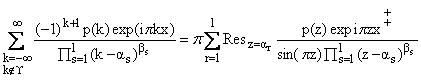
|
(3) |
где {bs},(s = 1, ..., l) - множество положительных
целых чисел, p(z) - многочлен степени, не выше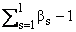 и принято
обозначение
и принято
обозначение
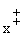 = (x + 1) (mod 2) - 1, -1 <
= (x + 1) (mod 2) - 1, -1 <
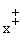 < 1.
< 1.
Доказательство основано нa рассмотрении интеграла
от функции под знаком вычетов в (3) по контуру прямоугольника с центром в точке
z = 0 и со сторонами Re(z) = ±(N + 1/2), Im(z) = ±(N + 1/2), где N - достаточно большое целое. При N ® Ґ этот интеграл стремится к нулю,
откуда, как нетрудно убедиться, следует формула (3) (подробности см. в [8], где
приведено доказательство несколько более простой
формулы).
Правая часть (3) есть 2-периодичная
функция, являющаяся на сегменте x О (-1,1) квазиполиномом, т.е. линейной комбинацией функций вида
{Pk(x) exp(ipakx)}, где {Pk(x)} - многочлены,
отвечающие множеству ¡ и кратным степеням {bs}, bs і 2. В случае {as
} = {0}, p(x) = 1, это - многочлен Бернулли Bb
0(x) (см.
[2,4,8]).
3. В данной
работе выдвигается идея реализации аналогичной КЭГ-методу схемы, с
предварительным применением классической аппроксимации Паде к формуле
(2).
Действительно, при каждом
зафиксированном s слагаемые первой суммы в (2) являются, - с точностью до
множителя (-1)n+1exp(ipnas)/(ipn), - отрезком
степенного асимптотического ряда относительно переменной z = 1/( ipn) и , следовательно , они могут быть заменены
аппроксимантом Паде порядка [m/N], m + N = Q (см. [9]), что и приводит к формуле
|
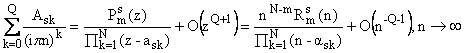
|
(4) |
где
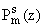 и
и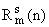 - многочлены (от z и n соответствено) степени, не
выше m, {ask} - нули знаменателя аппроксиманта Паде
(предполагается,что они отличны от нуля ), {ask} - возникающие после указанного преобразования
постоянные и s = 1, ј , l.
- многочлены (от z и n соответствено) степени, не
выше m, {ask} - нули знаменателя аппроксиманта Паде
(предполагается,что они отличны от нуля ), {ask} - возникающие после указанного преобразования
постоянные и s = 1, ј , l.
Остальные построения вполне аналогичны КЭГ - методу. Именно, применив
выше-приведенную лемму для каждого s (= 1, ј , l), можно представить функцию f в виде
f(x) = UQ(x) + w(x), где UQ(x) - соответствующая
кусочно-гладкая функция, состоящая из сдвигов квазиполиномов (и полиномов
Бернулли, если в (4) N < m), а w(x) Q раза непрерывно дифференцируема на
действительной оси и 2-периодична.
Естественно ожидать, что предлагаемая адаптивная аппроксимация таким
гибким инструментом, каким является система квазиполиномов, должна привести к
новым алгоритмам повышенной точности.
Назовем
предлагаемый метод квазиполиномиальным (QP-методом).
4. Численные эксперименты, проведенные применением
компьютерной системы MATHEMATICA 4.1 ([13]), полностью подтвердили эффективнисть
QP - метода. Для иллюстрации его свойств рассмотрим следующие две функции:
| f(x) = log(3 + i x cos(20x - 1)), g(x) = f(x) + |
(1 + i)exp(14 i x)
x + 1.15
|
+ exp(1 - 100 i x). | |
(5) |
Коэффициенты Фурье для последней (чисто экспоненциальной) добавки в g
вычислялись явно, а для других частей функций f и g они вычислялись применением
автоматического интегрирования , с погрешностью не более 10-11.
QP-метод
применялся на основе формулы (4) при N = m + 1 (парадиагональная аппроксимация Паде,
см. [9]). Скачки Ak = A1k (k = 0 ј , 2N - 1) вычислялись как точно, так и
приближенно, посредством решения линейной системы, получаемой (как и
рекомендовано в [2]), удалением суммы интегралов из (2) при Q = 2N - 1, для разных значений n = nr, (r = 1,ј,2N), 64 Ј nr Ј 128.
Таблица 1
Равномерные ошибки восстановления функции f(x) на отрезке
[-1,1] с
использованием ее коэффициентов Фурье
{fn}, |n| Ј 128
|
|
|
N=1 |
N=2 |
N=3 |
N=4 |
N=5 |
N=6 |
N=7 |
|
|
| Berr |
2.5e-4 |
7e-6 |
3e-7 |
1.8e-8 |
3e-6 |
2.5e-2 |
1.5e+2 |
| QPerr |
2e-4 |
7e-6 |
3e-7 |
1.8e-8 |
4e-9 |
1.2e-9 |
8e-10 |
|
|
| EBerr |
6e-5 |
2.5e-7 |
2.5e-9 |
1.5e-9 |
7e-7 |
1e-3 |
1.8e+0 |
| EQPerr |
1.8e-4 |
1.5e-7 |
1.4e-9 |
1.4e-11 |
4e-13 |
1.2e-14 |
8e-15 |
Таблица 2
Равномерные ошибки восстановления функции g(x) на отрезке
[-1,1] с
использованием ее коэффициентов Фурье
{gn}, |n| Ј 128
|
|
|
N=1 |
N=2 |
N=3 |
N=4 |
N=5 |
N=6 |
N=7 |
|
|
| Berr |
8e-2 |
2.5e-2 |
4e-3 |
5e-4 |
5e-2 |
1.2e+2 |
1.2e+5 |
| QPerr |
8e-2 |
2.5e-2 |
4e-3 |
5e-4 |
6e-4 |
6e-6 |
5e-7 |
|
|
| EBerr |
1.8e-2 |
7e-3 |
3e-5 |
3e-5 |
3e-2 |
5e+1 |
5e+4 |
| EQPerr |
2.5e-2 |
1.6e-4 |
4e-8 |
1.6e-10 |
5e-12 |
4e-13 |
4e-13 |
|
В приведенных
таблицах через Berr (QPerr) и
EBerr (EQPerr) обозначены равномерные ошибки при
применении классической схемы (см. [2]) КЭГ-метода (QP - метода), соответственно
на основе приближенного и точного вычисления коэффициентов {Ak}.
Отметим, что здесь, - при данном N, - WQ (см.
выше, пункт 1) является линейной комбинацией полиномов Бернулли
{Bk(x)}, k = 1, ј ,2N, a UQ (см.
пункт 3) - комбинацией из N квазиполиномов.
На этом примере просматривается явное преимущество QP-метода не только в
смысле точности и устойчивости. Так, при N = 6 и приближенном вычислении скачков
{Ak} для g, в представлении функции UQ содержится сумма
(0.02 - 0.01 i)exp((-6.1 + 12.6 i)x) + (0.52 -
0.2 i)exp((1.52 - 99.58 i)x), а при точном
вычислении этих скачков - сумма (2.1 + 0.14 i)exp((-1.26 + 13.03 i)x) + exp((1 - 100 i)x) (все постоянные даны с точностью до
10-3). При этом относительная ошибка при
приближенном вычислении скачков меняется от 10-6 для A0 до 100 для
A11. Ясно видно что ,- даже при значительных ошибках при определении
скачков высших производных ,- квазиполиномиальные (и близкие к ним) составляющие
функции g (и особенно - периоды осцилляций) практически эффективно
восстнавливаются. Отметим также, что здесь возмущение осцилляционной суммы
(g - f) неосцилляционным слагаемым f весьма существенно
(терминах L2 - норм ||g - f|| = 4.01 и ||f|| = 1.58).
При наличии точек {ak} как на концах, так и внутри отрезка [-1,1], ситуация вполне аналогична.
5. В заключение
приведем основные свойства QP - метода и наметим некоторые перспективы его
применения и развития.
· Даже при приближенном вычислении скачков
{Ask} кусочно-квазиполиномиальные функции практически точно
восстанавливаются посредством конечного числа коэффициентов Фурье, а если f
является суммой функции, близкой (в определенном смысле) к квазиполиномиальной,
и гладкой на отрезке [-1,1] функции, то почти
квазиполиномиальная часть (если ее "вклад" весом) восстанавливается
приближенно, в виде квазиполинома (см. пункт 4).
· QP-метод очевидным образом распространяется на
случай, когда известно дискретное преобразование Фурье значений функции f на
равномерной сети, поскольку и здесь (см. выше, п.1) скачки Ak
приближенно восстанавливаются.
· Предыдущие свойства крайне важны с прикладной
точки зрения. Фактически мы имеем инструмент, позволяющий приближенно выявить в
сигнале конечной длины (или в данных иного характера) как любые (а не только
кратные основной!) частоты содержащихся колебаний с заметной энергией, так и
режимы их затухания (нарастания).
· QP-метод гораздо устойчивей, - особенно по
отношению к возмущениям скачков {Ak},- чем КГЭ-метод. Его
преимущество, вообще говоря, резко возрастает с увеличением точности вычисления
скачков {Ak} (см. табл. 1 и 2).
· QP-метод можно применить
к отдельно взятым действительным и мнимым частям функции, к четным и нечетным ее
частям, к коэффициентам Фурье - Хартли и т.п. (из-за нелинейного характера
аппроксимации Паде эти подходы разные).
· Многомерный случай, в принципе, также может быть
включен в схему QP-метода. Например, если гладкая
функция f(x) задана на квадрате x О [-1,1] × [-1,1], то можно основываться
на асимптотической формуле для ее коэффициентов Фурье типа формулы (7) работы
[12]. Наличие сингулярностей у f внутри квадрата, разумеется, требует отдельного
изучения.
· Применение к асимптотическомы ряду (2) обобщенных
аппроксимаций Паде на основе производящих функций (см. [9-11]) может привести к
аппроксимации новыми системами кусочно-гладких функций.
· Идея QP-метода представляется применимой и к
разложениям кусочно-гладких функций по собственным функциям некоторых граничных
задач для дифференциальных уравнвний, собственные значения которых являются
нулями целых функций экспоненциального типа. Такова, например, задача Штурма -
Лиувилля (в том числе и сингулярная, см. [14]), обладающая дискретным
спектром.
Институт математики НАН РА
Литература
1. Крылов А. Лекции по приближенным вычислениям. Л. Изд. АН СССР. 1933.
2. Eckhoff K. S. - Math. Comp. 1995. V. 64. N. 210. P. 671-690.
3. Baszenski G., Delvos F. J., Tasche M. - Computers Math. Applic. 1995. V. 30. N. 3-6. P. 33-49.
4. Eckhoff K. S., Wasberg C.
E. - Report no. 99. Dept. of Math. University of Bergen. 1995. P.
1-38.
5. Gottlieb D., Shu C. W.
- Math. Comp. 1992. V. 43. P. 81-92.
6. Gelb A., Gottlieb D. - Computers Math.
Applic. 1997. V. 33. N. 11. P. 35-58.
7. Geer J., Banerjee N. S. - Journal of Scientific
Computing. 1997. V.12. N. 3. P. 253-287.
8.
Нерсесян А. Б., Оганесян Н. В. - Изв. НАН Армении.
Математика. 2002. T. 37. N. 5. C. 40-57.
9.
Бейкер Дж., Грейвс-Моррис П. Аппроксимации Паде. М.
Мир. 1986. 502 c.
10. Gammel J.
L., Rousseau C. C., Saylor D. P. - J. Math. Anal. Appl. 1967. V.
20. P. 416-420.
11. А. Б.
Нерсесян - ДНАН Армении. 2003. T. 103. N. 4. C. 279-285.
12. Nersessian A., Poghosyan
A. In: The Complex Analysis, Differention Equations and Related
Topics, G. A. Barsegian, H. G. W. Begehr, H. G. Ghazaryan, A. Nersessian, eds.
"Gitutjun" Publishing House. Yerevan. 2004. P. 70-78.
13. Wolfram S. The MATHEMATICA book. Fourth Edition. Wolfram Media. Cambridge
University Press. 1999. 1468 p.
14. Титчмарш Э. Ч. Разложения по собственным функциям,
связанные с дифференциальными уравнениями второго порядка. Часть 1. М.-Л. ИЛ.
1960. 278 c.
![]() Bk(t)dt = 0, k = 1,2,ј. На всю действительную ось многочлены {Bk(x)}
продолжаются периодически, с периодом 2, и являются кусочно-полиномиальными
функциями с коэффициентами Фурье Bk,n = (-1)n+1/ (2(ipn)k+1), n = 0, ± 1, ± 2, ј.
Bk(t)dt = 0, k = 1,2,ј. На всю действительную ось многочлены {Bk(x)}
продолжаются периодически, с периодом 2, и являются кусочно-полиномиальными
функциями с коэффициентами Фурье Bk,n = (-1)n+1/ (2(ipn)k+1), n = 0, ± 1, ± 2, ј.![]() =-Nwneipn x сходится к f со скоростью порядка o(N-Q), N ® Ґ.
=-Nwneipn x сходится к f со скоростью порядка o(N-Q), N ® Ґ.![]() и принято
обозначение
и принято
обозначение
![]() = (x + 1) (mod 2) - 1, -1 <
= (x + 1) (mod 2) - 1, -1 <
![]() < 1.
< 1.![]() и
и![]() - многочлены (от z и n соответствено) степени, не
выше m, {ask} - нули знаменателя аппроксиманта Паде
(предполагается,что они отличны от нуля ), {ask} - возникающие после указанного преобразования
постоянные и s = 1, ј , l.
- многочлены (от z и n соответствено) степени, не
выше m, {ask} - нули знаменателя аппроксиманта Паде
(предполагается,что они отличны от нуля ), {ask} - возникающие после указанного преобразования
постоянные и s = 1, ј , l.