УДК 515.1

   Статья посвящена бесконечномерной гомотопической топологии вещественного гильбертова пространства H. В ней определяется одна модификация важного классического топологического понятия пары Борсука [1]. Модифицированные пары (X,A) называются K₀-парами Борсука. Они образуются множествами A М X М H, а рассматриваемые отображения принадлежат одному специальному классу K₀ непрерывных отображений подмножеств из H.
   В работе приводятся некоторые свойства K₀-пар Борсука в случае сепарабельного гильбертова пространства.
   1. Допустимые отображения. В этом пункте приводятся определения допустимых отображений и некоторых необходимых понятий, а также сведения, относящиеся к этим отображениям [2-5].
   Рассмотрим произвольное вещественное гильбертово пространство H.
   Определение 1. Непрерывное отображение f : G ® H открытого в H множества G в H называется K₀-отображением, если выполнено следующее условие: (K₀) для любой точки x₀ О G и любого вещественного числа e > 0 существуют окрестность U М G точки x₀, линейное конечномерное подпространство L М H и вещественные числа l и d О (0,[(p)/2]) такие, что если для точек x,y О U угол между вектором x - y и подпространством L не меньше [(p)/2] - d, то выполнено соотношение

||f(x) - f(y) - l(x - y)|| Ј e||x - y||.

   Важным характеризующим свойством K₀-отображений является тот факт, что фигурирующее в условии (K₀) число l можно выбрать так, чтобы оно зависело лишь от точки x₀, но не от числа e. Получающаяся при этом единственная, непрерывная вещественнозначная функция l(x) = l_f(x), x О G, называется терминальной производной отображения f : G ® H; композиция двух K₀-отображений есть K₀-отображение и из ортопроекторов p : H ® L K₀-отображением являются только те, когда L-конечномерно или имеет конечную коразмерность относительно H.
   Пусть теперь M - произвольное (необязательно открытое) подмножество из H. Непрерывное отображение f : M ® H называется K₀-отображением, если существуют открытое в H множество G, содержащее M и K₀-отображение g : G ® H такое, что f(x) = g(x) для любого x О M.
   Пусть далее M и N - произвольные подмножества пространства H. Непрерывное отображение f : M @ N называется K₀-отображением, если композиция i o f : M ® H является K₀-отображением, где i : N ® H есть вложение. Наконец, гомеоморфизм f:M @ N называется K₀-гомеоморфизмом, если оба отображения f и f^-1 : N ® M суть K₀-отображения.
   Определение 2. Семейство (f_z), 0 Ј t Ј 1 K₀ -отображений f_t : M ® N называется K₀-гомотопией, если отображение F : I × M ® N, определяемое формулой F(t,x) = f_t(x), x О M, t О I, I = [0,1], является K₀-отображением.
   Далее, K₀-отображения f,g : M ® N называются K₀-гомотопными и пишут f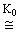g, если существует связывающая иx K₀-гомотопия, т.е. такая K₀-гомотопия (f_t), что f₀ = f и f₁ = g. Эквивалентным образом f,g называются K₀-гомотопными, если существует K₀-отображение F : I × M ® N такое, что F(0,x) = f(x) и F(1,x) = g(x) для каждой точки x О M.
   Определение 3. Декартово произведение X × Y подмножеств из H называется K₀-допустимым, если скалярное произведение x|y = 0 для любых точек x О X, y О Y и обе проекции (x,y) ® x и (x,y) ® y являются K₀-отображениями.
   Определение 4. Пусть A М X М H. Множество A называется K₀-ретрактом множества X, если существует K₀-отображение r : X ® A, называемое K₀-ретракцией X на A, такое, что r|A = id_A, т.е. roi = id_A, где i : A ® X есть вложение; ретракт A называется K₀-деформационным ретрактом для X, если существует такая K₀-ретракция r : X ® A, называемая K₀-деформационной ретракцией, что выполнено условие: i o r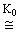id_X; если эта K₀-гомотопия будет неподвижной, т.е. связанной на A, то r называется K₀-строгой (или сильной) деформационной ретракцией, а A называется K₀-строгим (сильным) деформационным ретрактом для X.
   Существуют окрестностные варианты этих ретрактов, а именно: A называется окрестностным K₀-ретрактом, окрестностным K₀-деформационным ретрактом и окрестностным K₀-строгим деформационным ретрактом для X, если существует такое открытое в X подмножество U Й A, что A является соответственно K₀-ретрактом, K₀-деформационным ретрактом и K₀-строгим деформационным ретрактом для U.
   Определение 5. Непрерывное отображение f : M ® H будем называть локальным K₀-отображением, если существует такое открытое покрытие (U_a), a О A, подпространства M, что при любом a О A ограничение f_a = f|U_a : U_a ® H отображения f является K₀-отображением, т.е. существуют открытое в H подмножество G_a и K₀-отображение g_a : G_a ® H такое, что g_a|U_a = f_a.
   Имеет место важное утверждение: в случае сепарабельного гильбертова пространства H отображение f : M ® H будет K₀-отображением тогда и только тогда, когда оно является локальным K₀-отображением [см. 4].
   2. О K₀-парах Борсука. Пусть H - произвольное зафиксированное вещественное гильбертово пространство H. В этом пункте вводится одна модификация топологического понятия пары Борсука для пар подмножеств пространства H и устанавливается ряд свойств таких пар.
   Определение 6. Пусть A и X - подмножества из H; K₀-отображение i : A ® X будем называть K₀-корасслоением или обладающим свойством распространения K₀-гомотопий, если для любого подмножества Y из H, любого K₀-отображения f : X ® Y и K₀-гомотопии g_t : A ® Y, такой, что g₀ = f o i, существует такая K₀-гомотопия f_t : X ® Y , что f = f₀ и f_t o i = g_t для каждой точки t О I, I = [0,1].
   Композиция двух K₀-корасслоений есть также K₀-расслоение.
   Мы будем рассматривать важный частный случай понятия K₀-корасслоения - понятие K₀-пары Борсука.
   Определение 7. Пару (X,A) подмножеств пространства H будем называть K₀-парой Борсука, если отображение включения i : A ® X представляет собой K₀-корасслоение.
   Таким образом, пара (X,A) есть K₀-пара Борсука, если для каждого Y М H, K₀-отображения f : X ® Y и частичной гомотопии g_t : A ® Y отображения f, (g₀ = f|A), существует K₀-продолжение K₀-гомотопии g_t, т.е. такaя K₀-гомотопия f_t : X ® Y, что f₀ = f и f_t|A = g для каждой t О I.
   Из сказанного выше следует, что если (X,A,B) - такая тройка подмножеств из H, что пары (X,A) и (A,B) суть K₀-пары Борсука, то и пара (X,B) будет также парой Борсука.
   Однo из важных свойств K₀-пар Борсука состоит в следующем: пусть (X,A) - K₀-пара Борсука, g, g^ў : A ® Y суть K₀-гомотопныe K₀-отображения; тогда если одно из этих отображений продолжимо до K₀-отображения X в Y, то и другое K₀-продолжимо.
   Из сказанного следует, что свойство K₀-распространимости до X K₀-отображения g : A ® Y зависит от K₀-гомотопического классa отображения g.
   Приведем эквивалентную форму определения понятия K₀-пары Борсука.
   Определение 8. Пару (X,A) подмножеств из H будем называть K₀-парой Борсука, если для любого подмножества Y из H, K₀-отображения f : X ® Y, K₀-гомотопии G : I ×A ® Y такой, что G(0,x) = f(x) для каждой точки x О A, существует K₀-отображение F : I × X ® Y такое, что F(0,x) = f(x) для каждой точки x О X и F(t,x) = G(t,x) при t О I и x О A.
   В оставшейся части статьи пространство H будет предполaгаться сепарабельным, т.е. обладающим счетным базисом.
   Определение 9. Пара (X,A) подмножеств из H называется парой, допускающей терминальные производные, если подмножествa A и X являются множествами, допускающими терминальные производные [6].
   Теорема 1. Для того, чтобы допускающая терминальные производные пара (X,A) была K₀-парой Борсука, необходимо и достаточно, чтобы подмножество Ã = (O × X) И (I × A) цилиндра I × X было K₀-ретрактом для I × X.
   Топологическую пару (Z,C) принято называть замкнутой, если подпpостранство C замкнуто в Z. Поскольку гильбертово пространство H хаусдорфово, то из теоремы 1 можно заключить, что K₀-пара Борсука (X,A) есть замкнутая пара.
   Предложение 1. Пусть (X,A) - замкнутая пара, допускающая терминальные производные, и Y М H такое подмножество из H, для которого декартовы проиведения X × Y и A × Y являются K₀-допустимыми [см. опр. 3], тогда пара (X × Y, A × Y) является K₀-парой Борсука.
   Замечание. Предложение 1 верно также для пары (Y × X, Y × A), в частности для пары I × X,I × A.
   Предложение 2. Пусть X = A И B, где множества A,B и C = A З B замкнуты в X и являются множествами, допускающими терминальные производные. Тогда, если пара (A,C) является K₀-парой Борсука, то и (X,B) также является K₀-парой Борсука.
   Предложение 3. Пусть (X,A) - замкнутая пара, допускающая терминальные производные, и A есть K₀-деформационный ретракт подпространства X. Тогда, если пара (I × X,X_A), где X_A = (O × X) И (I × A) И (1 × X), является K₀-парой Борсука, то A будет K₀-строгим деформационным ретрактом подпространства X.
   Предложение 4. Пусть (X,A) - замкнутая и допускающая терминальные производные K₀-пара Борсука. Если A является K₀-слабым деформационным ретрактом подпространства X, то A будет K₀-деформационным ретрактом подпространства X.
   Определение 10. Подмножество A подпространства X называется окрестностным K₀-строгим деформационным ретрактом в слабом смысле подпространства X, если существуют такие открытые в X множества U Й A и такая K₀-гомотопия g_t : U ® X, что g_t неподвижнa на A, g₀(x) = x для каждой точки x О U и g₁(x) О A для x О U (см.п.1).
   В теореме 2 приводится локальная характеристика K₀-пар Борсука.
   Теорема 2. Пусть X,A - замкнутая и допускающая терминальные производные пара. Тогда, если (X,A) является K₀-парой Борсука, то A является окрестностным K₀-строгим деформационным ретрактом в слабом смысле подпространства X.
   Обратно, если A является K₀-строгим деформационным ретрактом в слабом смысле некоторого открытого в X подмножества U Й A и существует K₀-функциая Урысона j : X ® I пары A,X\U и A = j^-1(0), то (X,A) будет K₀-парой Борсука.
   Следствие. Пара (B,S) состоящая из единичного замкнутого шара B и единичной сферы S пространства H является K₀-парой Борсука.
   В самом деле, в соответствии с теоремой 2 надо положить U = B\{0}, K₀-гомотопию g_t : U ® B определить по формуле g_t(x) = (1 - t)x + t[x / (||x||)], а в качестве функции j : B ® I рассмотреть функцию j : x ® 1 - ||x||².