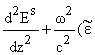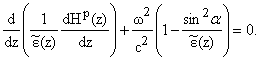ФИЗИКА
УДК 467
Н. М. Испирян
Распространение электромагнитной волны в произвольной
неограниченной периодической среде
(Представлено академиком Д. М. Седракяном 18/V 2004)
В последнее время возрос интерес к теории
распространения волн в периодических слоистых средах, что в основном обусловлено
новыми технологическими успехами в разработке пассивных и активных
тонкопленочных волноводов, а также твердотельных, оптических и акустических
решеток, получивших большое практическое применение [1-3].
В данной работе нами рассматривается задача
определения спектра собственных мод линейно поляризованной плоской
электромагнитной волны, распространяющейся в произвольной одномерной
неограниченной периодической среде. Для данной среды изменение диэлектрической
проницаемости в пространстве в наиболее общем виде может быть представлено
следующим образом:
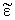 (z) = (z) = |
Ґ
е
n=-Ґ
|
e(z - Ln)q(nL - z)q[z - (n - 1)L], | |
(1) |
где L - период среды, e(z) - произвольная функция, q(z) -
ступенчатая функция Хевисайда.
Для удобства
при выводе уравнения, определяющего спектр собственных мод системы (1),
предположим, что между двумя произвольными соседними элементами периодической
среды существует бесконечно малая область, в которой диэлектрическая
проницаемость равна единице:
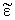 (z) = 1, где nL - 0
< z < nL + 0, (n = 0,±1, ±2,...). (z) = 1, где nL - 0
< z < nL + 0, (n = 0,±1, ±2,...). | |
(2) |
Как
мы увидим ниже, данное предположение никоим образом не влияет на окончательный
результат. Однородность среды в областях пространства (2) позволяет
рассматривать в них волновое поле
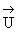 (
(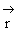 ,t) в виде суммы распространяющихся в противоположных
направлениях гармонических во времени плоских линейно поляризованных мод:
,t) в виде суммы распространяющихся в противоположных
направлениях гармонических во времени плоских линейно поляризованных мод:
|
®
U
|
( |
®
r
|
,t) = |
®
n
|
Re[y(z)exp{ik0xx}exp{-iwt}], | |
(3) |
| y(z) = An-1exp{ik0zz} + Bn-1exp{-ik0zz}, | |
(4) |
где для проекций волнового вектора
на оси z и x введены обозначения
| k0z = |
w
c
|
cosa,
k0x = |
w
c
|
sina. | |
Единичный
вектор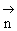 определяет направление поляризации волны. Заметим, что в (3)
предполагается, что волновой вектор расположен в плоскости
(z,x).
определяет направление поляризации волны. Заметим, что в (3)
предполагается, что волновой вектор расположен в плоскости
(z,x).
С учетом (3), (4) волновое уравнение
для s-волн удобно записать с помощью напряженности электрического поля, в то
время как для p-волн - с помощью напряженности магнитного поля
|
®
E
|
( |
®
r
|
,t) = (0,Es(z)exp{ik0xx}exp{-iwt},0], | |
(5.a) |
|
®
H
|
( |
®
r
|
,t) = (0,Hp(z)exp{-ik0xx}exp{-iwt},0]. | |
(5.b) |
Для полей Es(z) и
Hp(z) волновые уравнения имеют следующий вид [4]:
|
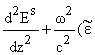 (z)sin2a)Es = 0, (z)sin2a)Es = 0, | |
(6) |
|
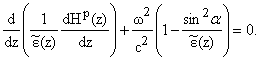
|
(7) |
Из (3), (4) и (6), (7)
непосредственно следует, что функция y(z), в
зависимости от поляризации волны
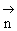 , определяет или Es(z), или Hp(z), т.е.
, определяет или Es(z), или Hp(z), т.е.
Согласно известной теореме Блоха,
решение волнового уравнения для периодической среды должно удовлетворять
следующему условию [4]:
где u(z) периодическая с периодом L
функция, а величина b называется квазиволновым числом.
Как мы покажем ниже, условие (9), а также
знание амплитуды прохождения волны для структурного элемента периодической среды
позволяют полностью определить спектр собственных мод. Для этого запишем связь
между коэффициентами решения (4) в точках nL и (n + 1)L через матрицу переноса
одного структурного элемента периодической системы (см., например, [4]):
где tns,
rns и tnp, rnp
являются амплитудами прохождения и отражения для s- и p-волн для n-ого
структурного элемента, граничащего с обеих сторон с вакуумом. Так как
структурные элементы периодической среды идентичны, то для них амплитуды
прохождения электрона совпадают, в то время как амплитуды отражения отличаются
фазовым множителем [6]:
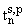 = ts,p, = ts,p,
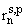 = rs,pexp{i2k0zL(n - 1)}, = rs,pexp{i2k0zL(n - 1)}, | |
(11) |
где через ts,p и
rs,p обозначены амплитуды рассеяния волны для первого (n = 1)
структурного элемента среды.
С учетом (11)
матричное соотношение (10) может быть записано в следующем виде:
An =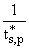 An-1 - An-1 -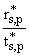 exp{-i2k0zL(n - 1)}Bn-1, exp{-i2k0zL(n - 1)}Bn-1, | |
(12) |
| Bn = - |
rs,p
ts,p
|
exp{i2k0zL(n - 1)}An-1 + |
1
ts,p
|
Bn-1. | |
(13) |
Будем искать решение системы уравнений (12), (13) в следующем виде:
| An = A0exp{i(b - k0z)nL}, Bn = B0exp{i(b + k0z)nL}, | |
(14) |
где b -
квазиволновое число (см. (9)). Подставляя (14) в (12), (13) и требуя, чтобы это
выполнялось для произвольного n, для величин A0, B0
получим следующую систему линейных однородных уравнений:
(1 /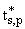 - exp{i(b - k0z)L})A0 - ( - exp{i(b - k0z)L})A0 - (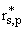 / /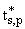 )B0 = 0, )B0 = 0, | |
(15) |
| (-rs,p/ts,p)A0 + (1/ts,p - exp{i(b + k0z)L})B0 = 0. | |
(16) |
Из (15), (16) следует, что волновое
поле определяется с точностью до одной произвольной постоянной. Требование
нетривиальности решения системы уравнений (15), (16) дает
| exp{i2bL} - exp{ibL} · 2Reлexp{-ik0z}/ts,pы + 1 = 0. | |
(17) |
При выводе (17) мы учли
Из
(17) непосредственно следует, что
| cos(bL) = Reлexp{-ik0zL}/ts,pы. | |
(18) |
Требование действительности
квазиволнового числа b приводит к неравенству
Неравенство (19) с учетом (18) дает
спектр собственных мод плоской электромагнитной волны для произвольной
одномерной неограниченной периодической среды. Как видно из (18), знание
амплитуды прохождения волны для структурного элемента среды непосредственно
приводит к уравнению, определяющему спектр мод.
Рассмотрим частный случай периодической среды, когда структурный элемент
представляет собой систему из двух однородных слоев, т.е
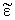 (z) = (z) = |
м
н
о |
|
| |
(20) |
где n = 0,±1,±2,ј. В
этом случае амплитуды прохождения s- и p-волн имеют вид [7]
|
1
ts
|
= exp(ik0zd) |
м
н
о |
cos(kzd) + i |
kz2 - k0z2
2kzk0z
|
sin(kzd) |
ь
э
ю |
, | |
(21) |
|
1
tp
|
= exp(ik0zd) |
м
н
о |
cos(kzd) + i |
(kz2/e) - (e·k0z)
2kzk0z
|
sin(kzd) |
ь
э
ю |
, | |
(22) |
где kz = (w/c)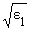 cosg и
cosg и
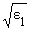 sing = sina. Подставляя (21), (22) в
(18), имеем
sing = sina. Подставляя (21), (22) в
(18), имеем
| cos(bsL) = cos[k0z(L - d)]cos(kzd) - |
k0z2 + kz2
2k0zkz
|
sin[k0z(L - d)]sin(kzd), | |
(23) |
| cos(bpL) = cos[k0z(L - d)]cos(kzd) - |
ek0z2 + kz2/e
2k0zkz
|
sin[k0z(L - d)]sin(kzd). | |
(24) |
Уравнения (23), (24) являются
известными классическими уравнениями, определяющими квазиволновые числа bs и bp s- и
p-волн для неограниченной периодической системы со структурным элементом,
состоящим из двух однородных слоев [7].
Автор
выражает благодарность академику Д. М. Седракяну, а также А. Ж. Хачатряну за
полезное обсуждение полученных результатов.
Государственный инженерный университет
Армении
Литература
1. Karlsson A., Stewart R. -
J. Opt. Soc. Am. A. 1995. V. 12. P. 1513.
2. Elson J. M., Tran P. -
J. Opt. Soc. Am. A. 1995. V. 12. P.
1766.
3. James S. P., Tatam R.
T. - Meas. Sci. Technol. 2003. V. 14. P.
49.
4. Борн М., Вольф Э. Основы оптики. М. Наука. 1973.
5.
Sedrakian D. M., Gevorgyan A. H., Khachatrian A. Zh. - Optics Communication. 2001. V. 192. P. 135.
6. Бреховских Л. М. Волны в слоистых средах.
М. Наука. 1973.
7. Ярив А., Юх
П. Оптические волны в кристаллах. М. Мир. 1987.
![]() (
(![]() ,t) в виде суммы распространяющихся в противоположных
направлениях гармонических во времени плоских линейно поляризованных мод:
,t) в виде суммы распространяющихся в противоположных
направлениях гармонических во времени плоских линейно поляризованных мод: ![]() определяет направление поляризации волны. Заметим, что в (3)
предполагается, что волновой вектор расположен в плоскости
(z,x).
определяет направление поляризации волны. Заметим, что в (3)
предполагается, что волновой вектор расположен в плоскости
(z,x).![]() , определяет или Es(z), или Hp(z), т.е.
, определяет или Es(z), или Hp(z), т.е.