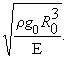When the cross-section area S(x) of the cable
is the function of cable length (tapered cable), using the dimensionless
notations the equation determining the cable elastic stress s(x) can be written as,
|
d[S(x)s(x)]
dx
|
+ S(x)F(x) = 0, | |
(3) |
| F(x) = rg0R0g(x),
g(x) = |
é
ê
ë |
a(1 + x) - |
1
(1 + x)2
|
|
ù
ú
û |
. | |
(4) |
Here the following dimensionless
notations are used:
x = g/R0,
L = l/R0, a = w2R0/g0 » 1/288, l is the cable length.
Coefficient a characterizes the ratio of the gravity and centrifugal
accelerations on the Earth surface. For the Mars and the Moon this coefficient
equals to
Equation (3) is to be considered with the following boundary condition
at free end
When
S(x)=const, the elastic stress is defined by the following function, satisfying
to (3-5)
s(x) = rg0R0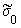 (x), (x), |
|
(6) |
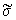 (x) = (x) = |
(L - x)[(1 + L)(1 + x)(2 + L + x) - 576]
576(1 + L)(1 + x)
|
. | |
Since function
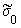 (x) may
have only one zero in the interval x Î [0,L], then from
condition
(x) may
have only one zero in the interval x Î [0,L], then from
condition
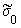 (0) = 0, (1 + L)(2 + L) = 576
, follows that for all L ³ L0 = 22.5
(0) = 0, (1 + L)(2 + L) = 576
, follows that for all L ³ L0 = 22.5
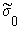 (x) ³ 0,
x Î
[0,L0]. (x) ³ 0,
x Î
[0,L0]. | |
(7) |
Therefore, when the length of the cable is more than
l0 = 143.325 km the cable is in a pure tension state. For cables with
L = L0, s(0) = 0 and mechanical tension stress
reaches its maximum value s0 » 0.78rg0R0,
at point x0 » 5.602 (where
g(x0) = 0), which corresponds to the Earth geosynchronous orbit g0 = 35.785 km. For cables with L ³ L0, we have the following condition
supx[s(x)] ³ s0.
Let us note
that the "limit" lengths for space elevator cable located on the Mars or the
Moon equators are the following:
| L01 = 19.38
(l01 = 65698)
km | |
| L02 = 17.21
(l02 = 29893)
km | |
To minimize the cable maximum tension stress and its critical length we
need to consider a tapered cable, cross-section area of which is the function of
cable length S = S(x).
Based on solution of equation (3) the stress function can be written as
s(x) =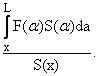
|
|
(8) |
The solution (8) satisfies the
boundary condition (5) at a free end.
Let us consider the cable with the following
cross section area function
S*(x)S0exp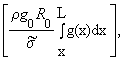 |
|
(9) |
where
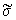 is a constant one.
is a constant one.
Substituting (8) into (9)
leads to
s(x) =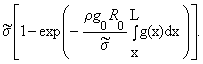 |
|
(10) |
From (10) follows that analogous to the case of the non tapered cable,
s(x ³ 0), when L ³ L0 » 22.4; for
L = L0, s(0) = 0 and mechanical tension stress
reaches to its maximum value at x0 » 5.60
max s(x) =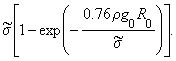 |
|
(11) |
On the other hand we have
|
max S* = S0exp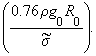 |
|
(12) |
From (12), (13) one can note that
where h is
a tapering ratio of the cable, s0 = 0.76rg0R0 is the maximum stress of the of
non tapered cable.
On the cable ends we have
Based on formula (13) the dependence of the maximum stress value from
tapering ratio is given in Table 1. As it follows from Table 1. data, the
thickening of the cable at the point of the Earth geosynchronous orbit leads to
the decreasing of the maximum tension stress. E.g. for a continuous cable of a
circular cross section the two times increase of the cable radius at the
geosynchronous orbit point leads to the two times decrease of the maximum
stress.
Table 1
Dependence of Maximum Stress upon Tapered
Ratio
| h |
1.1 |
1.6 |
2.5 |
4 |
8 |
10 |
20 |
| x |
0.95 |
0.79 |
0.65 |
0.54 |
0.42 |
0.39 |
0.31 |
The above-mentioned results determine the projects of the cable design
when the "limit" length does not change, while the cable form permits decrease
of maximum stress.
We can reach the
decreasing both the "limit" length and the maximum stress by appropriate choice
of the cross section area function. Let us consider the cross section area
functions as the quadratic polynomial functions of the following type
| S(x) = S0 |
é
ê
ë |
1 + |
ax
L
|
+ |
bx2
L2
|
|
ù
ú
û |
, | |
(14) |
where a,b are arbitrary
constants.
Substituting (14) into (8), we
obtain the stress function depending upon parameters a,b. Since the stress
function expression is very cumbrous we do not present it
here.
By means of numerical analysis of this
expression the cable forms, namely, parameters a,b are determined, providing the
implementation of the following conditions
| s(x) ³ 0, |
max
x
|
s(x) |
®
S
|
|
min
|
| |
These numerical
results for two considered cases are the following:
cable "limit" length
L0 = 18, (b = -1.04, a = 2.0), maxxs(x) = 0.61rg0R0,
cable "limit" length
L0 = 16.0, (b = -2.2, a = 4.23), maxxs(x) = 0.52rg0R0.
Let us now consider the cable
with a "counterweight" of mass M0 attached to its outward end. In
this case, we have the following boundary condition
| g(L) = |
é
ê
ë |
|
(1 + L)
288
|
- |
1
(1 + L)2
|
|
ù
ú
û |
. | |
(15) |
The stress function satisfying the
boundary condition (15) is the following
s(x) = rg0R0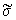 (x) (x) |
|
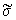 (x) = (x) = |
(L - x)[(1 + L)(1 + x)(2 + L + x) - 576]
576(1 + L)(1 + x)
|
+ |
M0L
M
|
|
é
ê
ë |
|
(1 + L)
288
|
- |
1
(1 + L)2
|
|
ù
ú
û |
, | |
(16) |
where M0 = rLR0S0 is the cable mass.
When the
"counterweight" of mass M0 is attached to the cable outward end, it
is possible to consider a design of uniformly tensioned cable when mechanical
stress is constant along the cable length. Such a design for a ponderable rod
was considered first by S. Timoshenko [2].
Seeking in equation (1) solution
s(x) = const we come to the following solution for the
cable cross-section area function.
| S*(x) = S0exp |
é
ê
ë |
|
rg0R0
s*
|
|
L
ó
õ
x
|
g(x)dx |
ù
ú
û |
, | |
(17) |
where
g(x) is the function
defined by (4), S0 is the cable cross-section area at the outward
end, where the mass M0 is attached. For a cable with "limit" length
L0 = 22.4 function S(x) reaches to its maximum value S* at
point x » 5.60.
The maximum value of the (17) can be
written as
On
the other hand we have
where s0 = 0.76rg0R0 is the maximum stress of the of
non tapered cable. From (18), (19) follows that decrease of the maximum stress
leads to exponential increase of S*. E.g. when b = 2, we have S* = 7.39S0. For a
continuous cable of a circular cross section, it means that the cable radius
increase 2.7 times.
Table 2
"Limit" lengths and stress maximum values in depend of the
"counterweight" mass
| M/M0 |
100 |
50 |
20 |
10 |
5 |
2 |
1 |
| L0 |
22.3 |
22.07 |
21.0 |
20.48 |
19.2 |
16.2 |
13.2 |
| s0 |
0.76 |
0.74 |
0.66 |
0.63 |
0.53 |
13.2 |
0.22 |
The "counterweight" decreases slightly the "limit" length and stress
maximum values, when M >> M0. In the contrary, the
"counterweight" decreases essentially the "limit" length and stress maximum
values, when the cable mass is compared with "counterweight" mass.
Let us
now consider the elastic stability problem in the non tapered cable when its
length is less than "limit" length, L < L0. In this case the
compression stresses arise localized near cable base and due to it, the cable
may become unstable.
The cable elastic
stability equation and appropriate boundary conditions can be written as
|
d4W
dx4
|
- l |
d
dx
|
|
é
ê
ë |
|
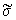 0 0
|
(x) |
dW
dx
|
|
ù
ú
û |
= 0; | |
(20) |
| W|x=0 = 0,
|
dW
dx
|
|
ê
ê
ê |
x=0
|
= 0, | |
|
d2W
dx2
|
|
ê
ê
ê |
x=L
|
= 0, |
d3W
dx3
|
|
ê
ê
ê |
x=L
|
=0, | |
(21) |
where the dimensionless function
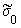 (x) is defined as in (6), EI is
the bending rigidity of the cable material, W(x) transverse displacement of the
elastic cable, l º rg0R03S0(EI)-1. Using notation y(x) = [dW/dx], integrating equation
(20) and taking into consideration the boundary conditions we come to the
following equation and boundary conditions
(x) is defined as in (6), EI is
the bending rigidity of the cable material, W(x) transverse displacement of the
elastic cable, l º rg0R03S0(EI)-1. Using notation y(x) = [dW/dx], integrating equation
(20) and taking into consideration the boundary conditions we come to the
following equation and boundary conditions
|
d2y
dx2
|
0 - l |
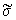 0 0
|
(x)y = 0, | |
(22) |
| y|x=0 = 0,
|
dy
dx
|
|
ê
ê
ê |
x=L
|
= 0. | |
(23) |
Equation (22) with conditions (23)
is the self-adjoint boundary value problem determining eigenvalues l. Since the function
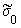 (x) changes its sign in the interval x
Î [0,L], the eigenvalues can be both positive and
negative ones. The minimum positive eigenvalue l0 corresponds to the critical load behind which
the cable becomes unstable.
(x) changes its sign in the interval x
Î [0,L], the eigenvalues can be both positive and
negative ones. The minimum positive eigenvalue l0 corresponds to the critical load behind which
the cable becomes unstable.
Let function
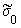 (x) change its sign from a negative
value to a positive one at point x0.
(x) change its sign from a negative
value to a positive one at point x0.
Then for minimum positive
eigenvalue, l0 the following inequality is
valid
where function
y0(x) is any admissible function satisfying to the conditions
y0(0) = y0(x0) = 0.
Let us consider the cable
with L = 22.0. For this cable x0 = 0.04; and taking
y0(x) = x(x - x0) we come to the
inequality l0 < 6326. Based on this
inequality we can postulate that for a rod with circular cross section of radius
r when r < r0 the elastic rod under consideration is unstable,
where
r0 = 0.025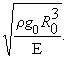 |
|
Therefore, the
solution of the self-adjoint boundary value problem (22-23) even in this case
(L = 22.0) results in the instability of the cable for any values of elastic and
geometrical parameters having practical and science forecasting meanings.
Conclusions.
Based on
the solution of the one dimension equation of the elasticity theory qualitative
and quantitative results are obtained related to strength and stability problems
of a space elevator cable/ribbon. It is assumed that the cable is subjected to
action of the Earth gravity inward force, defined by Newton gravity law and the
centrifugal outward force, due to the Earth's daily spinning. The numerical data
related to the strength characteristics of new modern materials such as carbon
nanotubs are omitted, since these data are in [1]. We confined ourselves to
results related to the tapered cable design strength problems. Based on the
solution of a one dimension elasticity equation solution of the tensile strength
does not determine an absolute value of cable cross-section area. This cross
section value parameter may be determined while considering the two dimensional
problems or dynamics problems, especially elastic wave propagation along a
tensioned cable.
On the other hand, there is no doubt that the future objects
of the investigation should be constructions of elastic closed shells (pipes)
type, which are of interest from an applied point of view. For such
constructions, the new mechanical problems should be considered, which take into
account circular, transversal stresses and displacements arising in the shells.
Among these problems we can list the dynamic interaction of closed shells
subject to external media, including electromagnetic, temperature and atmosphere
fields actions.
Institute of Mechanics of NAS RA
Ëèòåðàòóðà
1. B. C. Edvards, E. A.
Westling - The Space Elevator. Houston. USA.
2002.
2. S. Timoshenko - The Strength of Materials. Fizmatgiz. Moscow. 1965.
![]() (x),
(x),![]() (x) =
(x) =![]() (x) may
have only one zero in the interval x Î [0,L], then from
condition
(x) may
have only one zero in the interval x Î [0,L], then from
condition
![]() (0) = 0, (1 + L)(2 + L) = 576
, follows that for all L ³ L0 = 22.5
(0) = 0, (1 + L)(2 + L) = 576
, follows that for all L ³ L0 = 22.5 ![]() (x) ³ 0,
x Î
[0,L0].
(x) ³ 0,
x Î
[0,L0].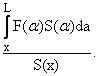
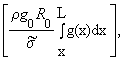
![]() is a constant one.
is a constant one.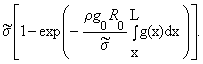
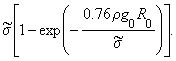
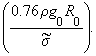
![]() (x)
(x)![]() (x) =
(x) =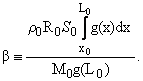
![]() 0
0![]() (x) is defined as in (6), EI is
the bending rigidity of the cable material, W(x) transverse displacement of the
elastic cable, l º rg0R03S0(EI)-1. Using notation y(x) = [dW/dx], integrating equation
(20) and taking into consideration the boundary conditions we come to the
following equation and boundary conditions
(x) is defined as in (6), EI is
the bending rigidity of the cable material, W(x) transverse displacement of the
elastic cable, l º rg0R03S0(EI)-1. Using notation y(x) = [dW/dx], integrating equation
(20) and taking into consideration the boundary conditions we come to the
following equation and boundary conditions ![]() 0
0![]() (x) changes its sign in the interval x
Î [0,L], the eigenvalues can be both positive and
negative ones. The minimum positive eigenvalue l0 corresponds to the critical load behind which
the cable becomes unstable.
(x) changes its sign in the interval x
Î [0,L], the eigenvalues can be both positive and
negative ones. The minimum positive eigenvalue l0 corresponds to the critical load behind which
the cable becomes unstable.![]() (x) change its sign from a negative
value to a positive one at point x0.
(x) change its sign from a negative
value to a positive one at point x0.