MECHANICS
ÓÄÊ 539.3
M. V. Belubekyan, E. O. Chil-Akopyan
On a Problem of the Located Instability of Compound Plate
(Submitted by academician S. A Ambartsumian 3/III 2004)
The problem of instability of two rectangular
plates connected by the hinge, when one of them is compressed, is investigated.
Let two semi-infinite plates-strips connected
by the hinge at x = 0, and fixed by the hinge on edges y = 0, b, when one of them is
compressed towards 0y by the load of intensity P0.
The equations of instability problem with
regard to flexure wi, selected according to the theory of thin plates
and based on Kirchhoff hypothesis [1], are following:
| D2D2w2 + P0 |
¶2w2
¶y2
|
= 0 (x < 0),
D2w1 = 0
(x > 0), | |
(1) |
| Di = |
2Eihi3
3(1-ni2)
|
,
i = 1,2, | |
where
Di - flexural rigidities, wi - flexures, Ei -
modules of elasticity, ni - Poisson's
ratios, D- two-dimensional operator of Laplace.
As conditions of contact are used well-known
in structure mechanics conditions, when on a line of contact x = 0, plates are
connected by the hinge [2], i.e. bending moments are equal to zero.
| D1 |
¶
¶x
|
|
é
ê
ë |
|
¶2w1
¶x2
|
+ (2 - n1) |
¶2w1
¶y2
|
|
ù
ú
û |
= D2 |
¶
¶x
|
|
é
ê
ë |
|
¶2w2
¶x2
|
+ (2 - n2) |
¶2w2
¶y2
|
|
ù
ú
û |
. | |
(5) |
The
conditions (3), (4) represent the equality of bending moments
(M1(1) = M1(2)) to zero, condition (5)
the equality of generalized over cutting forces
(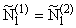 ) of
contacting plates.
) of
contacting plates.
It is required to find the solutions of the
equations (1) which are satisfying boundary conditions (2)-(5) and conditions of
damping on infinity.
|
lim
x®+¥
|
w1 = 0, |
lim
x®-¥
|
w2 = 0. | |
(6) |
If
the equations of instability problem have not trivial solutions which are
satisfying boundary conditions, when x = 0, y = 0, b and the conditions of damping
on infinity, we can call that solutions located by the edge x = 0. If such kinds
of solutions exist, we can say that the located instability of a plate takes
place.
Let's present the solutions (1) which are
satisfying the conditions at y = 0, b, (wi = 0, [(¶2w2)/(¶y2)]) as follows:
| wi = Win(x)sinlny, ln = np/b,
n = 1,2,... | |
(7) |
Substituting (7) into (1) we obtain the ordinary differential equations
of the fourth order for definition Win(x):
| W1nIV - 2ln2W1nII - ln4W1n = 0, | |
(8) |
| W2nIV - 2ln2W2nII - ln4(1 - a2n2)W2n = 0, | |
where
From
the common solutions of the equations (8) we shall choose just satisfying to a
condition (6).
where
| P3 = |
Ö
|
1 + a1n
|
, P4 = |
Ö
|
1 + a2n
|
. | |
(11) |
Also the realization of condition 0 £ a2n2 £ 1 of
existence of the localized solution is necessary. Substitution (10), (with the
account (7)) in the boundary conditions (2)-(5), results in system of the
homogeneous algebraic equations concerning any constants A, B, C, E.
where
|
ì
ï
ï
ï
í
ï
ï
ï
î |
|
|
| A · ln · (1 - n1) - 2 · B = 0 | |
| C · (P32 - n2) + E · (P42 - n2) = 0 | |
| A · c · ln · (1 - n1) + B · c · (1 + n1) - | |
| -C · ln(P33 - (2 - n2)P3) - E · ln(P43 - (2 - n2)P4) = 0. | | |
| |
(13) |
Equating to zero a determinant of a system
and after lines of transformations we come to the following dispersive equation:
| L(a2n)
º (P4 - P3) · L1(a2n) = 0, | |
(14) |
where
| L1(a2n) = |
ì
í
î |
2 · (P32P42 + 2(1 - n2)P3P4 - n22) + c(P4 + P3)(3 - 2 · n1 - n12) |
ü
ý
þ |
. | |
(15) |
As
P3 = P4 only at a2n = 0,
and taking into the consideration the fact that the root of the equation (14) at
a2n = 0 is trivial, in the given task in stead
of (14) we shall consider the following equation:
This function L1(a2n) = 0
has the following properties:
| L1(0) = 2 · (1 + 2(1 - n2) - n22) + 2 · c · (3 - 2n12 - n12) >
0. | |
(17) |
In
this case for the existence of the located instability it is necessary that:
L1(1) = -2n22 +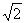 · c · (3 - 2n12 - n12) <
0. · c · (3 - 2n12 - n12) <
0. | |
(18) |
Hence, we can say that the located instability takes place at the
observance of the following condition:
| c < |
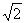 · n22 · n22
3 - (2 + n1) · n1
|
= c* | |
The numerical results are given in the table.
| n1 |
n2 |
c* |
| 0.1 |
0.1 |
0.005 |
| 0.1 |
0.2 |
0.1 |
| 0.2 |
0.2 |
0.022 |
| 0.2 |
0.1 |
0.005 |
| 0.1 |
0.3 |
0.1 |
| 0.3 |
0.3 |
0.1 |
| 0.3 |
0.3 |
0.055 |
| 0.4 |
0.4 |
0.111 |
| 0.5 |
0.5 |
0.020 |
In this table are
given the values of the parameter c* for
various Poisson's ratios, which are satisfying to condition (19).
From the data resulted in the table it is
visible, that the located instability exists since the value of c < 0.202 for the natural conditions (0 £ n1 £ 0.5, 0 £ n2 £ 0.5) and
substantially depends on Poisson's ratios: n1 and n2.
Similar problems for one plate and for two
compressed plates connected by the hinge, have been investigated in [3, 4]
accordingly. Institute of Mathematics of NAS
RA
![]() ) of
contacting plates.
) of
contacting plates.![]() · c · (3 - 2n12 - n12) <
0.
· c · (3 - 2n12 - n12) <
0.![]() · n22
· n22