ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
УДК 517.518.4, 517.518.8, 517.538.3
Академик А. Б. Нерсесян, А. В. Погосян
Об одной линейной рациональной аппроксимации
на
конечном отрезке
(Представлено 16/II 2004)
1. Введение. Восстановление гладкой на конечном отрезке функции f(x), x
О [-1,1], с использованием
конечного числа ее коэффициентов Фурье
| fn = |
1
2
|
|
у
х |
1
-1
|
f(x)e-ipn xdx, n = 0,±1±2,ј,±N, 0 <
N < Ґ | |
(1) |
является одной из классических
задач.
В теории тригонометрических рядов
(см.[1]) основное внимание обращено на свойства отрезка ряда Фурье
SN(f) и остатка RN(f)
| SN(f)(x) := |
N
е
n=-N
|
fneipn
x, RN(f)(x) := f(x) - SN(f)(x). | |
(2) |
Однако SN(f), N >> 1, является оптимальным
аппаратом приближения к f(x) на [-1,1] (будь то в
равномерной или иной разумной метрике) лишь в случае, когда f(x) продолжается на
ось x О (-Ґ,Ґ), как периодическая функция (с
периодом 2), без потери гладкости. В противном случае локальная сходимость в
окрестностях точек x = ±1 оказывается гораздо более
медленной (а при f(1) № f(-1)
и вовсе отсутствующей из-за явления Гиббса), чем вдали от этих точек.
Среди многочисленных работ, посвященных
эффективным альтернативным подходaм, отметим те, которые являются развитием
идеи, использованной в работе А. Крылова [2] и в дальнейшем развитой в работах
Д. Готтлиба и Экгофа ([3,4]) на основе использования многочленов Бернулли.
С другой стороны, заметной эффективностью
обладает метод Фурье - Паде (см. [5,6]), однако он является существенно
нелинейным.
В предложенной работе используется подход,
близкий к методу Фурье - Паде, однако являющийся линейным и,- в определенном
смысле,- оптимальным при аппроксимации гладкой на всем отрезке [-1,1] функции f(x) рациональной тригонометрической функцией с
использованием коэффициентов {fn}, |n| Ј N.
Основным аппаратом данного исследования
является построение "предельной функции", впервые изученной Валле-Пуссеном еще в
1908 г. (см. [8]).
2. Постановка задачи.
Рассмотрим конечное число комплексных чисел в виде вектора q := {qk}pk=-p, p і 1 и
положим
D0n(q) = fn, Dkn(q) =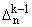 (q) + qk sgn(n) (q) + qk sgn(n)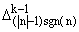 (q), k і
1, (q), k і
1, | |
(3) |
где sgn(n) = 1 при n і 0 и sgn(n) = -1 при n < 0.
Запишем (2) в виде
| RN(f)(x) = R+N(f)(x) + R-N(f)(x), | |
| R+N(f)(x) := |
Ґ
е
n=N+1
|
fneipn
x, R-N(f)(x) := |
-N-1
е
n=-Ґ
|
fneipn
x. | |
Примeнением
преобразования Абеля легко убедиться, что в случае |q1| № 1
После p-кратного
повторения такого преобразования приходим к следующему разложению ошибки
R+N(f)(x) (|qk| № 1, k = -p,ј,p):
Аналогичные
разложения для RN-(f)(x) приводят
к следующей формуле:
Sp,N(q,f)(x) :=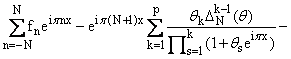 |
|
-e-ip(N+1)x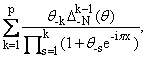 |
|
(4) |
которую будем считать
аппроксимационной, с ошибкой
Rp,N(q,f)(x) := f(x) - Sp,N(q,f)(x) =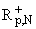 (q,f)(x) + (q,f)(x) +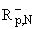 (q,f)(x), (q,f)(x), | |
(5) |
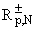 (q,f)(x)
:= (q,f)(x)
:= |
|
(6) |
Наша
задача состоит в минимизации равномерной ошибки Rp,N(q,f) на всем отрезке [-1,1]
соответствующим выбором параметров {qk}.
Отметим, что если параметры {qk} определять
из следующих двух систем:
| Dnp(q) = 0, n = -N - p, ј, -N - 1; n = N + 1, ј, N + p, | |
(7) |
то придем к хорошо известной
аппроксимации Фурье - Паде [N + p/p]f.
3. Теоретические результаты. 3.1. Пусть f О Cq[-1,1]. Обозначим
| Ak(f) = f(k)(1) - f(k)(-1),
k = 0, ј, q. | |
(8) |
Теорема 1 [9]. Пусть f О
Cq[-1,1], q і
0, f(q+1) О L1[-1,1] и Aj(f) = 0 для j = 0, ј, q - 1. Тогда при x = 1 - [h/N], h = const і 0
|
lim
N® Ґ
|
NqRN(f) |
ж
з
и |
1 - |
h
N
|
ц
ч
ш |
= Aq(f)Lq(h), | |
(9) |
| Lq(h) = |
(-1)q
pq+1
|
|
у
х |
Ґ
1
|
|
xq+1
|
. | |
(10) |
В
данном случае (см. [1]) равномерная ошибка на [-1,1]
характеризуется величиной
В таблице 1 представлены значения
этой величины для различных значений
q.Таблица 1
Равномерные ошибки при аппроксимации рядом Фурье
для
различных значений q.
| q |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| lq |
0.5 |
0.101321 |
0.012382 |
0.003421 |
0.000744 |
0.000208 |
0.000052 |
3.2. Проведем теперь
аналогичные исследования для аппроксимации Sp,N(q,f). Сначала докажем несколько
лемм.
Лемма 1 Пусть
| wk,m := |
k
е
s=0
|
Cks(-1)s sm, 0 Ј m Ј
k, | |
(12) |
где
Cks = [k!/(s!(k - s)!)]. Тогда
Доказательство. Обозначим
| jk,0(z) := (1 + z)k = |
k
е
s=0
|
Ckszs, jk,m(z) := z jўk,m-1(z), m і
1. | |
Теперь достаточно
заметить, что jk,m(-1) = wk,m.
Далее,
через gk(p),k = 0, ј, p, обозначим, коэффициенты следующего полинома:
|
p
Х
k=1
|
(1 + tk x)
є |
p
е
k=0
|
gk(p)
xk. | |
(14) |
Лемма 2 Пусть f О
Cq+p[-1,1], q і
0, p і 1, f(q+p+1) О L1[-1,1] и Aj(f) = 0 для j = 0, ј, q - 1. Если
| qk = q-k = 1 - |
tk
N
|
, k = 1, ј, p, | |
(15) |
то имеет место следующее
асимптотическое разложение
| Dnp(q) = Aq(f) |
(-1)n+p+1
2 (ip)q+1q!
|
|
p
е
k=0
|
|
(q + p - k)!(-1)kgk(p)
Nk(n - k)q+1|n - k|p-k
|
+ o(n-q-p-1) | |
(16) |
при N ® Ґ, |n| і N + 1.
Доказательство.
Если в (??) взять qk є 1, |k| Ј p, то положим Dnk := Dnk(q). Это
хорошо известные классические конечные разности.
По индукции легко показать, что
|
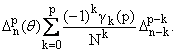
|
(17) |
Снова по индукции
| Dnk = |
k
е
j=0
|
Ckjf(|n|-j)sgn(n), Ckj = |
k!
j!(k - j)!
|
. | |
(18) |
Для получения асимптотики
коэффициентов Фурье проинтегрируем по частям (1), p + q + 1 раза
| fn = |
(-1)n+1
2
|
|
p+q
е
s=q
|
|
As(f)
(ipn)s+1
|
+ |
1
2(i pn)p+q+1
|
|
у
х |
1
-1
|
f(p+q+1)(x)e-ipn
xdx, | |
(19) |
где последнее слагаемое имеет
порядок o(n-p-q-1) при n ® Ґ согласно хорошо известной теореме Римана - Лебега [1].
Согласно (18) пoлучим
| Dnk = |
(-1)n+1
2
|
|
p+q
е
s=q
|
|
As(f)
(ipn)s+1
|
|
k
е
j=0
|
Ckj |
(-1)j
|
+ o(n-p-q-1) | |
(20) |
при n ®
Ґ и 0 Ј k Ј p.
Далее, положим
gs(x) = (1 - x)-s-1. С помощью разложения в
ряд Тейлора и леммы 1 получим
|
k
е
j=0
|
Ckj |
(-1)j
|
= |
k
е
m=0
|
|
gs(m)(0)
m!|n|m
|
wk,m + o(n-k) = |
(k + s)!(-1)k
s!|n|k
|
+ o(n-k), n ® Ґ. | |
Подставив это в (20), получим
| Dnk = Aq(f) |
(-1)n+k+1(q + k)!
2 (ipn)q+1q! |n|k
|
+ o(n-k-q-1), n ® Ґ. | |
Это
вместе с (17) завершает доказательство.
3.3. Сначала изучим сходимость аппроксимации
Sp,N(q,f) внутри (вдали от концов) отрезка
[-1,1]. Следующую теорему легко доказать с помощью
леммы 2.
Теорема 2. Пусть f О Cq+p[-1,1], q і 0, p і 1, f(q+p+1) О
L1[-1,1] и Aj(f) = 0 для j = 0, ј, q - 1. Если qk = 1 - tk/N, tk
> 0 и |x| < 1, то для
достаточно больших N имеет место следующая оценка:
| Nq+p|Rp,N(q,f)| Ј const |Aq(f)|. | |
(21) |
Рассмотрим теперь поведение ошибки Rp,N(q,f)(x) в окрестности точки x = 1.
Теорема 3. Пусть f О
Cq+p[-1,1], q і
0, p і 1, f(q+p+1) О L1[-1,1] и Aj(f) = 0
для j = 0,ј,q - 1. Если
| qk = q-k = 1 - |
tk
N
|
, k = 1, ј, p, tk
> 0, tj № ti, j № i, | |
(22) |
тогда при x = 1 - [h/N], h = const і 0 имеет место
следующая асимптотическая формула:
|
lim
N®Ґ
|
NqRp,N(q,f) |
ж
з
и |
1 - |
h
N
|
ц
ч
ш |
= Aq(f)Lq,p(h), | |
(23) |
|
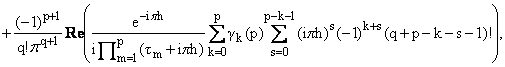
|
(24) |
а Lq(h) определено в
теореме 1.
Доказательство. Имеем
|
p
Х
k=1
|
(1 + qkeipx) = |
p
Х
k=1
|
|
ж
з
и |
1 + |
ж
з
и |
1 - |
tk
N
|
ц
ч
ш |
eip(1-[h/N]) |
ц
ч
ш |
= |
1
Np
|
|
p
Х
k=1
|
(tk + iph + O(N-1)), N ® Ґ. | |
Отсюда,
из леммы 2 и из (6) имеем
|
lim
N®Ґ
|
NqR+p,N(q,f) |
ж
з
и |
1 - |
h
N
|
ц
ч
ш |
=
| |
Остается
упростить полученную оценку, проинтегрировав по частям, и заметить, что
аналогичные выкладки имеют место и для R-p,N(q,f).
Сравнение теорем 2 и
3 показывает, что равномерная ошибка на отрезке [-1,1]
полностью определяется предельной величиной
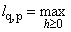 |Lq,p(h)|. |Lq,p(h)|. | |
(25) |
4. Численная оптимизация В настоящем пункте
равномерная ошибка lq,p минимизируется соответствующим выбором
параметров tk, k = 1, ј, p. Здесь эта задача решается для p = 1,2. Вычисления
реализованы примeнением пакета MATHEMATICA 5 [7]. Строго говоря, найденные
значения параметров могут и не являться наилучшими из возможных, однако
условимся называть их "оптимальными".
Сначала
рассмотрим случай p = 1. Элементарные вычисления показывают, что
| Lq,1(h) = Lq(h) - |
| t1
sinp |
ж
з
и
|
h + |
q
2
|
ц
ч
ш
|
+ hcosp |
ж
з
и
|
h + |
q
2
|
ц
ч
ш
|
pq+1(t12 + p2 h2)
|
. | |
(26) |
Оптимальные значения параметра
t1, полученные численной минимизацией
величины Lq,1, представлены в табл. 1. Отношение
lq/lq,1 показывает, насколько аппроксимация
Sp,N(q,f) с оптимальным выбором параметра
t1 эффективней, чем отрезок ряда Фурье
SN(f). Как видим, уже при q = 3 имеем разницу на порядок, в пользу
оптимального выбора.
Таблица 2
Значения констант lq,1,
lq/lq,1 (см. табл. 1)
для различных
значений q, при оптимальном выборе параметра t1
| q |
1 |
2 |
3 |
4 |
5 |
| lq,1 |
0.01525 |
0.00153 |
0.00026 |
0.00005 |
0.00001 |
| lq/lq,1 |
6.6 |
8 |
13.1 |
14.7 |
18.8 |
| t1 |
1.17728 |
2.23568 |
3.24768 |
4.26805 |
5.27982
|
Пусть теперь
p = 2. В этом случае
| Lq,2(h) = Lq,1(h) + |
| ( 1 - t1 + q ) |
ж
з
и
|
(t1 + t2 ) hp cosp |
ж
з
и
|
h + |
q
2
|
ц
ч
ш
|
+ (t1 t2 -
h2p2 )sinp |
ж
з
и
|
h + |
q
2
|
ц
ч
ш
|
ц
ч
ш
|
|
pq+1(t12 + p2 h2)(t22 + p2 h2)
|
. | |
(27) |
Оптимальные значения параметров t1,t2 и
соответствующие результаты представлены в табл. 2. Здесь разница между
аппроксимациями Sp,N(q,f) и SN(f)
уже достигает двух порядков. Заметим, что в этом случае минимизируется функция
трех переменных (h,t1,t2), что связано со значительными вычислительными
трудностями. Случаи p і 3, видимо, должны изучаться на
более мощных вычислительных системах, чем современные
ПК.
Таблица 3
Значения констант lq,2,
lq/lq,2 для различных значений q,
при
оптимальном выборе параметров t1 и t2
| q |
1 |
2 |
3 |
4 |
| lq,2 |
0.0054 |
0.0003 |
0.00026 |
7·10-6 |
| lq/lq,2 |
18.8 |
36.2 |
77.6 |
112.2 |
| t1 |
2.648 |
4.009 |
5.305 |
6.303 |
| t2 |
0.430 |
1.058 |
1.750 |
2.337 |
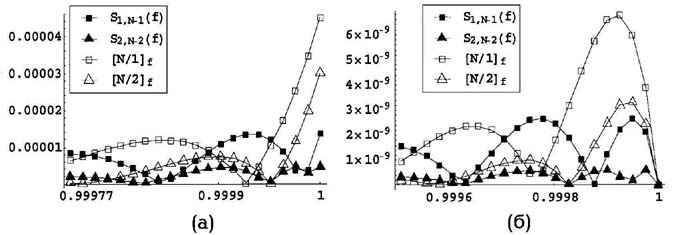
Интересно сравнить предлагаемую аппроксимацию
Sp,N(q,f) с аппроксимацией Фурье - Паде. На
рисунке представлены графики ошибок при аппроксимации двух функций: (1 - x2)sin(x - 1) (а) и (1 - x2)2
sin(x - 1) (б) при N = 2048. Здесь
сравниваются аппроксимации Sp,N(q,f),p = 1,2 с
"оптимальным" выбором параметров (см. табл. 1,2) и аппроксимации Паде
[N/p]f, p = 1,2. Как видно из рисунка, и здесь сравнение в
пользу аппроксимации Sp,N(q,f). Уместно
заметить, что аппроксимация Фурье - Паде связана с решением системы (7),
которая, как правило, плохо обусловлена, особенно при больших N и p. Кроме того,
это нелинейная аппроксимация, в отличие от предложенной
нами.
5. Заключение.
Представленные теоретические и численные результаты показывают, что
аппроксимации Sp,N(q,f) при оптимальном
выборе параметров {tk} более эффективны, по
сравнению как с частными суммами ряда Фурье, так и с аппроксимациями Фурье -
Паде. Эта разница тем больше, чем больше q. Поэтому, если для аппроксимируeмой
функции A0(f) № 0, то на практике желательно
воспользоваться хорошо известной схемой примeнения полиномов Бернулли (см.
введение) и только после этого использовать предложенную схему при q і 5.
|
|
Графики ошибок при аппроксимации функций
(1 - x2)sin(x - 1) (а) и (1 - x2)2
sin(x - 1) (б) при N = 2048.
Работа выполнена в рамках проекта ISTC A-823.
Институт математики НАН РА
Литература
1. Zygmund A. - Trigonometric Series. 1959. V. 1,2.Cambridge Univ.
Press.
2. Крылов А. Лекции по приближенным вычислениям, Изд-во АН СССР. Л. 1933.
3. Eckhoff K. S. - Math. of Computation. 1998. V. 67. N 223. P. 1363-1387.
4. Gottlieb D., Shu C. W. -
Numer. Math. 1996. V. 33. P. 280-290.
5. Baker G. A., Graves-Morris P. - Pade
Approximants, Encyclopedia of mathematics and its applications. 1996. V. 59.,
2nd ed., Cambridge Univ. Press., Cambridge.
6. Geer J. - ICASE report NO1995. 93-68;
J.Sci. Copm. V. 10(3). P. 325-356.
7. Wolfram S. The MATHEMATICA book. Fourth Edition, Wolfram
Media, Cambridge University Press. 1999.
8.
Vallee-Poussin Ch. J. de la - Bull. Acad. Roy,
Belgique. 1908. P. 319-410.
9. Нерсесян А. Б. Оганесян Н. В. - Изв. НАН Армении.
Математика. 2002. Т. 37. N. 5.
с.48-62.
![]() (q) + qk sgn(n)
(q) + qk sgn(n)![]() (q), k і
1,
(q), k і
1,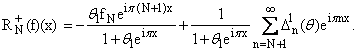
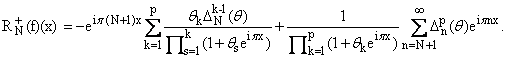
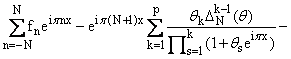
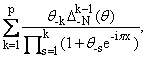
![]() (q,f)(x) +
(q,f)(x) +![]() (q,f)(x),
(q,f)(x),![]() (q,f)(x)
:=
(q,f)(x)
:=
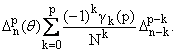
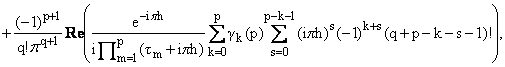
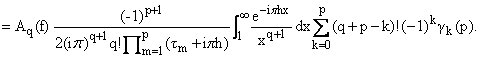
![]() |Lq,p(h)|.
|Lq,p(h)|.