ФИЗИКА
УДК 539.016
А. М. Ишханян
Вероятность перехода Ландау - Зинера при фотоассоциации
бозе-эйнштейновского конденсата в пределе слабого взаимодействия
(Представлено академиком Р.А. Казаряном 23/X 2003)
1. Система
полуклассических нелинейных уравнений, описывающих
двухмодовую фотоассоциацию [1] атомарного бозе-эйнштейновского конденсата [2],
имеет вид
i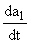 = U(t)e-id(t) = U(t)e-id(t) , i , i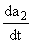 = =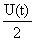 eid(t)a1a2, eid(t)a1a2, |
|
(1) |
где a1 и a2 -
амплитуды, соответственно, атомарного и молекулярного состояний, U = U(t) -
частота Раби, а d = d(t) -
функция модуляции расстройки. Это довольно общие уравнения, возникающие во всех
полевых теориях, оперирующих кубической нелинейностью (см., например, [3]). Тем
не менее, cистема крайне мало изучена. Точные аналитические решения известны
только для простейшей задачи Раби: U = U0 =
const, dt = d0 = | const, и
небольшого количества специфических моделей, полученных совсем недавно [4],
которые, однако, имеют довольно ограниченное применение.
Во всех же физически интересных случаях с
переменными функциями модуляции расстройки и/или частотами Раби приходится
обращаться к приближенным методам. Однако здесь мы наталкиваемся на трудности,
связанные с расходимостью получающихся поправочных членов. Можно попытаться
преодолеть эту трудность, переходя к уравнению, содержащему лишь вероятность. В
случае модели Ландау - Зинера U = U0 = | const; d = d0t2 [5,6]
интересующее нас уравнение для молекулярного состояния имеет вид [7]
| pўўў - |
pўў
t
|
+ 4[t2 + l(1 - 3p)]pў + |
l
2t
|
(1 - 8p + 12p2) = 0, | |
(2) |
где l =
U20/d0 - параметр
Ландау - Зинера. Однако, как показывает проверка, проблема с расходимостью
по-прежнему остается. Это означает, что следует, вообще говоря, обратиться к
иным - нетривиальным - методам возмущений, таким, как, например, усреднение
Крылова - Боголюбова - Митропольского или метод многих масштабов [8], которые
зарекомендовали себя как в высшей степени успешные при решении большого числа
задач во многих областях физики и математики. Подобный подход был нами применен
в [7], но следует отметить, что этот способ довольно сложный из-за того, что при
этом приходится привлекать высшие трансцендентные функции [9], поскольку
уравнение (2) третьего порядка.
Тем не менее, предложенные в работе [7]
выражения для конечной вероятности перехода стимулируют поиск альтернативных
подходов. По крайней мере, в пределе малых интенсивностей внешнего поля, l << 1, когда нелинейный член представляет собой слабое регулярное возмущение [8], подобный поиск представляется
вполне обоснованным. Руководствуясь этими соображениями, в предыдущей работе
[10] мы вывели некоторое нелинейное интегральное уравнение Вольтерра [11],
эквивалентное уравнению (2), которое позволяет избавиться от упомянутой
расходимости и построить окончательное решение в виде сходящегося ряда для
случая малых l. Примечательно, что такое преобразование
возможно для всех моделей с постоянной амплитудой поля.
Здесь следует отметить еще и то важное обстоятельство, что решения системы (1)
образуют классы [12]. Благодаря этому число принципиально
различных моделей сокращается до небольшого количества базовых моделей.
Рассматриваемая в настоящей работе модель Ландау - Зинера является одной из
таких основных моделей.
Следовательно, общее заключение таково, что
развитый в работе [10] подход может служить общей стратегией при решении
аналогичных нелинейных двухуровневых задач. В настоящей работе мы демонстрируем
эффективность данного подхода выводом простой формулы для первого поправочного
члена к нулевому приближению и расчетом конечной (на бесконечности) вероятности
перехода в молекулярное состояние для малых значений параметра Ландау - Зинера.
2. Нелинейное
интегральное уравнение Вольтерра второго рода [11], предложенное в работе [10],
можно записать в виде
| p(t) = |
l
4
|
f(t) - 4l |
t
у
х
-Ґ
|
K(t,x) |
ж
з
и |
p(x) - |
3
2
|
p2(x) |
ц
ч
ш |
dx, | |
(3) | где ядро K(t,x) задается формулой
| K(t,x) = (Cd(t) - Cd(x))cos(d(x)) + (Sd(t) - Sd(x))sin(d(x)), | |
(4) | а вынуждающая функция f(t) [11] имеет вид
| f(t) = Cd2(t) + S2d(t), Cd(t) = |
t
у
х
-Ґ
|
cos(d(x))dx, Sd(t) = |
t
у
х
-Ґ
|
sin(d(x))dx. | |
(5) | Если теперь функции f(t) и K(t,x)
ограничены, то последовательные приближения Пикара
| p0 = |
l
4
|
f(t), pn = |
l
4
|
f(t) - 4l |
t
у
х
-Ґ
|
K(t,x) |
ж
з
и |
pn-1 - |
3
2
|
pn-12 |
ц
ч
ш |
dx | |
(6) |
равномерно сходятся к предельной
функции p(t), которая и является единственным решением уравнения (3).
Для модели Ландау - Зинера функции
Cd(t) и Sd(t) принимают вид
| Cd(t) = |
ж
ъ
Ц
|
|
|
ж
з
и
|
|
1
2
|
+ C |
ж
з
и
|
|
ж
ъ
Ц
|
|
ц
ч
ш
|
ц
ч
ш
|
, Sd(t) = |
ж
ъ
Ц
|
|
|
ж
з
и
|
|
1
2
|
+ S |
ж
з
и
|
|
ж
ъ
Ц
|
|
ц
ч
ш
|
ц
ч
ш
|
, | |
(7) | где C и S являются функциями Френеля
[9], определяемыми как
| C(x) = |
x
у
х
0
|
cos |
ж
з
и |
p
2
|
x2 |
ц
ч
ш |
dx, S(x) = |
x
у
х
0
|
sin |
ж
з
и |
p
2
|
x2 |
ц
ч
ш |
dx. | |
(8) |
Интересно, что вынуждающая функция
уравнения Вольтерра при этом превращается в знаменитую функцию из теории
дифракции света:
| f(t) = |
p
2d0
|
|
м
н
о
|
й
к
л
|
1
2
|
+ C |
ж
з
и
|
ж
ъ
Ц
|
|
ц
ч
ш
|
щ
ъ
ы
|
2
|
+ |
й
к
л
|
1
2
|
+ S |
ж
з
и
|
ж
ъ
Ц
|
|
ц
ч
ш
|
щ
ъ
ы
|
2
|
ь
э
ю
|
. | |
(9) |
Как хорошо известно, эта функция
задает интенсивность света за полубесконечной непрозрачной стенкой, при этом t
играет роль бокового расстояния от края стенки [13].
Как было отмечено в работе [10],
последовательные приближения Пикара (6) с вынуждающей функцией (9) представляют
собой чересчур медленно сходящую процедуру. Это легко понять, заметив, что
нулевой член разложения (6) p0 = lf(t)/4 ® lp/4 при
t ® +Ґ, так что начиная уже с
l » 0.65 p0
превышает максимальное значение 1/2, допускаемое нормировкой. Нетрудно показать,
что и следующее приближение страдает подобным недостатком: оно становится
отрицательным при l > 0.65.
С целью улучшения сходимости предпочтительнее
предварительно применить к интегральному уравнению (3) подстановку
p = pL + u, где pL - решение линейного интегрального уравнения
pL = pLZ(t)/4. Записываемое часто [6] в функциях
параболического цилиндра [9] решение линейной задачи Ландау - Зинера [5] удобнее
всего может быть выражено через вырожденную гипергеометрическую функцию Куммера
следующим образом:
|
| a2LZ(t) = C1F1 + C2F2,
F1 = 1F1(il/4; 1/2/id0t2), | |
| F2 = t · 1F1(1/2 + il/4; 3/2; id0t2), | | |
| |
(10) |
|
| C1 = |
Ц
|
le-pl/4coshpl/4
|
|
i
2
|
|
G(1/2-il/4)
G(1-il/4)
|
, | |
| C2 = |
Ц
|
le-pl/4cosh(pl/4)
|
· |
Ц
|
id0
|
, | | |
| |
(11) | где G-
гамма-функция Эйлера. При t = +Ґ мы имеем хорошо
известный результат Ландау - Зинера
В результате мы приходим к новому уравнению
Вольтерра хаммерштейновского типа [11]
| u = 6l |
у
х |
t
-Ґ
|
K(t,x)pL2dx - 4l |
t
у
х
-Ґ
|
K(t,x)[(1 - 3pL)u - |
3
2
|
u2]dx | |
(13) |
с видоизмененной вынуждающей
функцией, которая теперь порядка l3.
Очевидно, что эта вынуждающая функция обеспечивает намного более быстрое
схождение аппроксимаций. Таким путем удается установить, что решение нелинейной
задачи Ландау - Зинера в режиме слабого взаимодействия в первом приближении
записывается в виде [10]
| p(t) = |
pLZ(t)
4
|
+ 6l |
t
у
х
-Ґ
|
K(t,x) |
ж
з
и |
pLZ(x)
4
|
ц
ч
ш |
2
|
dx. | |
(14) |
Как показывает численный расчет,
это очень хорошее приближение. Вплоть до l < 0.5 при
сравнении с численным решением системы (1) имеет место практическая
неразличимость графиков.
Примечательно также, что формула (14)
позволяет вычислить конечную (в пределе t ® +Ґ) вероятность перехода в молекулярное состояние
аналитически. Действительно, ведущий член в формуле (13) дает (далее будем
полагать d0 = 1)
| u(+Ґ) » 6l |
+Ґ
у
х
-Ґ
|
|
й
к
л
|
ж
з
и
|
ж
ъ
Ц
|
|
- Cd(x) |
ц
ч
ш
|
cosd(x) - |
ж
з
и
|
ж
ъ
Ц
|
|
- Sd(x) |
ц
ч
ш
|
sind(x) |
щ
ъ
ы
|
p2Ldx. | |
(15) |
Поскольку поправка u(t) - порядка l3, предварительную оценку можно получить
посредством замены pL на p0 = lf(t)/4. В этом случае легко получается, что на бесконечности
|
| p(+Ґ) = pL(+Ґ) + l3 |
ж
з
и |
- |
p3
16
|
+ |
3
8
|
|
ж
ъ
Ц
|
|
IG |
ц
ч
ш |
, | |
| IG = |
+Ґ
у
х
-Ґ
|
(cos(x2) + sin(x2))(Cd2(x) + Sd2(x) + Sd2(x))2dx. | | |
| |
(16) |
Приближенное аналитическое
вычисление интеграла приводит к IG » [(p2)/6]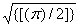 (2 + 0.9190) = 6.0179, что находится в неплохом согласии с
численным результатом IG = 5.8412. Таким образом, имеем оценку (2 + 0.9190) = 6.0179, что находится в неплохом согласии с
численным результатом IG = 5.8412. Таким образом, имеем оценку
| p(+Ґ) = |
PLZ
4
|
+ u(+Ґ) » |
PLZ
4
|
+ |
0.919p3
32
|
l3. | |
(17) | В качестве начального приближения
это выражение хорошо подтверждает формулу
| p(+Ґ) » |
PLZ(l)
4
|
|
ж
з
и |
1 + |
l
p
|
PLZ(l) |
ц
ч
ш |
. | |
(18) | Действительно, данная формула
приводит к
| p(+Ґ) = |
PLZ
4
|
+ |
p
4
|
l3 + O(l4). | |
(19) |
Так что разница мала уже в этом
приближении: 0.919p3/32 - p/4 » 0.1.
Однако результат можно существенно улучшить.
Это можно сделать, заметив, что линейное решение pL, присутствующее в
подынтегральном выражении (13), хорошо аппроксимируется формулой вида
где функция fL(t) не
зависит от l. Вид этой функции можно установить из
уравнения (2) следующим образом. Подставив в уравнение
p = PfinalfL(t), где Pfinal является конечной
вероятностью перехода при t ® +Ґ, и далее разделив его на Pfinal, можно получить
| fўўўL- |
fўўL
t
|
+ [4t2 + 4l(1 - 3PfinalfL)]fўL + |
l
2t
|
|
ж
з
и |
|
1
Pfinal
|
- 8fL + 12 |
Pfinal
4
|
f2L |
ц
ч
ш |
= 0. | |
(21) |
Теперь для вывода уравнения для
предельной функции fL(t) надо взять предел l ® 0, помня при этом, что l/Pfinal » l/(PLZ/4) = 4l/(1 - e-pl) ®
4/p:
| fўўўL- |
fўўL
t
|
+ 4t2fўL + |
2
pt
|
= 0. | |
(22) |
Частным решением этого уравнения,
удовлетворяющим рассматриваемым здесь начальным условиям, является
| fL(t) = - |
1
4
|
+ |
4(Cd + Sd)
p2
|
+ |
t2
2p
|
[2F2(1,1; 3/2,2; +it2) +
2F2(1,1; 3/2,2; -it2)]. | |
(23) | Подстановка этой функции в
уравнение (14) теперь дает
| p(+Ґ) = |
PLZ
4
|
+ l |
ж
з
и |
PLZ
4
|
ц
ч
ш |
2
|
I, | |
(24) | где
| I = 6 |
+Ґ
у
х
-Ґ
|
|
й
к
л
|
ж
з
и
|
ж
ъ
Ц
|
|
- Cd(x) |
ц
ч
ш
|
cosd(x) - |
ж
з
и
|
ж
ъ
Ц
|
|
- Sd(x) |
ц
ч
ш
|
sind(x) |
щ
ъ
ы
|
f2L(x)dx. | |
(25) |
Изучение подынтегрального выражения (25)
показывает, что оно эффективно отличается от нуля только в малом интервале в
окрестности начала координат. Хотя здесь возможно прямое аналитическое
рассмотрение, скажем, с помощью разложения в ряд, однако, учитывая, что этот
интеграл - всего лишь число, его просто можно рассчитать численно. В результате
получается значение I = 1.3317 » 4/3. Непосредственное
использование самого линейного решения Ландау - Зинера улучшает результат, давая
I = 1.3082, который должен заменить I в (24), тем самым подтверждая значение
I = 4/p » 1.2732, даваемое
формулой (18). Выведенная формула (24) с последним числом хорошо согласуется с
численным решением: относительная ошибка вплоть до l
» 0.4 остается меньше 10-3.
Таким образом, мы изучили нелинейную задачу
Ландау - Зинера для фотоассоциации атомарного бозе-эйнштейновского конденсата.
Применив нелинейное уравнение Вольтерра, мы вывели приближенное выражение для
конечной вероятности перехода в молекулярное состояние для случая слабого
взаимодействия - формулу (18). Поскольку рассмотренная здесь модель нелинейной
двухуровневой задачи является типовой для классических и бозонных теорий поля с
кубической нелинейностью, полученная формула может служить новой парадигмой для
нелинейных квантовых задач пересечения термов.
Работа выполнена при поддержке грантов Фонда
Гражданских Исследований и Разработок США (CRDF) No. NFSAT PH 100-02/12042.
Инженерный центр НАН РА
Литература
1. Javanainen J., Mackie J.
- Phys. Rev.A. 1999. V. 59. P. R3186; Kosatrun
M., Mackie M., Cote R., Javanainen J. - Phys. Rev.A.
2000. V. 62. P. 063616.
2. Anderson M.H., Ensher J.R., Matthews M.R., Wieman C.E., Cornell E.A.
Science. 1995. V. 269. P.198; Anglin J.R.,
Ketterle W. - Nature (London). 2002. V. 416. P.
211.
3. Timmermans E., Tommasini
P., Hussein M., Kernan A. - Phys.Rep.C. 1999. V. 315.
P. 199; Shen Y.R. The Principles of
Nonlinear Optics,
N. Y. Wiley. 2002.
4. Ishkhanyan A.M., Mackie M., Gould Ph., Javanainen J. In: Interactions in Ultracold Gases: From Atoms to Molecules (Eds. M.
Weidemuller and C. Zimmerman). Berlin. Wiley.
2003.
5. Landau L.D. - Phys. Z. Sowjetunion. 1932. V. 2. P. 46; Zener C.
- Proc. R. Soc. London A.1932. V. 137. P.
696.
6. B.W. Shore. The Theory of Coherent Atomic
Excitation. N. Y. Wiley. 1990.
7.
Ishkhanyan A.M., Mackie M., Carmichael A., Gould Ph., Javanainen
J. - Phys. Rev. A. 2004. V.
69.
8. Nayfeh A.H. Perturbation Methods. N. Y. Wiley-Interscience.
1985.
9. Abramowitz M., Stegun
I.A. Handbook of Mathematical Functions. N. Y. Dover.
1965.
10. Ishkhanyan A.M.,
Chernikov G.P. - J. Contemp. Physics (Armenian Nat’l Ac.
Sci.). 2004. V. 39(1). P.1.
11. Tricomi F.G. Integral Equations. N. Y. Dover
Publications. 1985; Miller R.K. Nonlinear Volterra Integral
Equations. N. Y. Benjamin. 1971.
12. Ishkhanyan A.M. - J. Phys. A. 2000. V. 33. P. 5539;
Ishkhanyan A.M. - Opt. Commun. 2000.V. 176. P.
155.
13. Sommerfeld A.
- Math. Ann. 1896. V. 47. P. 317; Born M.,
Wolf E. Principles of Optics. Cambridge. Cambridge University Press.
1999.
|